Sprawdzian Ulamki Zwykle Kl 5

Drogi uczniu klasy 5, rozumiem, że sprawdziany z ułamków zwykłych mogą wydawać się trudne i stresujące. Pamiętam, jak sam, kiedy byłem w Twoim wieku, patrzyłem na ułamki jak na coś skomplikowanego i nieprzystępnego. Ale wiedz, że z odpowiednim podejściem i solidną dawką ćwiczeń, ułamki mogą stać się Twoimi przyjaciółmi!

Ten artykuł ma za zadanie pomóc Ci przygotować się do sprawdzianu z ułamków zwykłych, zrozumieć, dlaczego warto je znać, i pokazać, że wcale nie są takie straszne, jak się wydają.

Dlaczego ułamki są ważne? To nie tylko szkolna teoria!

Zastanawiasz się, po co w ogóle uczyć się o ułamkach? Przecież w codziennym życiu używasz liczb naturalnych, a o ułamkach jakoś nie słychać... A jednak! Ułamki otaczają Cię z każdej strony:

Gotowanie: Przepis na ciasto wymaga ½ szklanki mąki, ¼ łyżeczki proszku do pieczenia. Bez ułamków, ciasto się nie uda!
Dzielenie się: Kiedy dzielisz pizzę ze znajomymi, każdy dostaje kawałek – czyli ułamek całej pizzy.
Mierzenie czasu: Godzina ma 60 minut. Pół godziny to 30 minut, kwadrans to 15 minut. To wszystko ułamki!
Zakupy: Połowa ceny towaru na przecenie, to ułamek ceny początkowej.

Jak widzisz, ułamki są niezbędne do funkcjonowania w świecie. Rozumiejąc je, będziesz mógł lepiej radzić sobie w codziennych sytuacjach, a także w dalszej edukacji.

Co musisz wiedzieć na sprawdzianie?

Rodzaje ułamków

Podstawowa wiedza to rozróżnianie różnych rodzajów ułamków:

Ułamek właściwy: Licznik jest mniejszy od mianownika. Na przykład: 1/2, 3/4, 5/8. Ułamek właściwy jest zawsze mniejszy od 1.
Ułamek niewłaściwy: Licznik jest większy lub równy mianownikowi. Na przykład: 5/4, 7/3, 8/8. Ułamek niewłaściwy jest większy lub równy 1.
Liczba mieszana: Składa się z liczby całkowitej i ułamka właściwego. Na przykład: 1 1/2, 2 3/4, 5 1/8. Liczbę mieszaną można zamienić na ułamek niewłaściwy i odwrotnie.

Pamiętaj! Ważne jest, aby umieć rozpoznać każdy rodzaj ułamka i wiedzieć, jak je zamieniać między sobą (np. zamiana liczby mieszanej na ułamek niewłaściwy).

Działania na ułamkach

Na sprawdzianie na pewno pojawią się zadania z dodawania, odejmowania, mnożenia i dzielenia ułamków.

Dodawanie i odejmowanie ułamków o jednakowych mianownikach: Dodajemy (lub odejmujemy) liczniki, a mianownik pozostaje bez zmian. Na przykład: 1/5 + 2/5 = 3/5, 4/7 - 1/7 = 3/7.
Dodawanie i odejmowanie ułamków o różnych mianownikach: Sprowadzamy ułamki do wspólnego mianownika, a następnie dodajemy (lub odejmujemy) liczniki. Na przykład: 1/2 + 1/3 = 3/6 + 2/6 = 5/6. Wspólny mianownik to najmniejsza wspólna wielokrotność mianowników.
Mnożenie ułamków: Mnożymy licznik przez licznik i mianownik przez mianownik. Na przykład: 1/2 * 2/3 = 2/6 = 1/3 (po skróceniu).
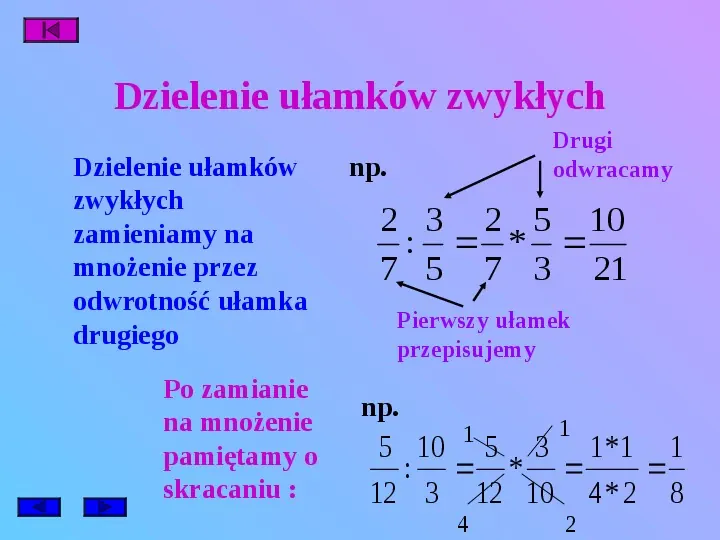
Dzielenie ułamków: Dzielenie ułamka to mnożenie przez jego odwrotność. Odwrotność ułamka to zamiana licznika z mianownikiem. Na przykład: 1/2 : 2/3 = 1/2 * 3/2 = 3/4.

Ćwicz! Ćwicz! Ćwicz! Im więcej zadań rozwiążesz, tym pewniej poczujesz się na sprawdzianie.

Skracanie i rozszerzanie ułamków

Skracanie ułamków: Dzielimy licznik i mianownik przez ten sam dzielnik różny od 1. Na przykład: 4/8 = 2/4 = 1/2. Skracanie ułatwia wykonywanie działań i doprowadza do najprostszej postaci ułamka.

Rozszerzanie ułamków: Mnożymy licznik i mianownik przez tę samą liczbę różną od 1. Na przykład: 1/2 = 2/4 = 3/6. Rozszerzanie jest potrzebne przy sprowadzaniu ułamków do wspólnego mianownika.

Znajdź największy wspólny dzielnik (NWD)! To ułatwi Ci skrócenie ułamka do najprostszej postaci.

Jak się przygotować do sprawdzianu?

Oto kilka sprawdzonych sposobów na efektywne przygotowanie się do sprawdzianu:

Powtórz teorię: Przeczytaj jeszcze raz podręcznik, notatki z lekcji, ten artykuł. Upewnij się, że rozumiesz definicje i zasady wykonywania działań.
Rozwiązuj zadania: Znajdź zadania w podręczniku, zbiorze zadań, w internecie. Rozwiązuj jak najwięcej różnych typów zadań.
Sprawdzaj odpowiedzi: Porównuj swoje rozwiązania z odpowiedziami w kluczu. Jeśli się pomylisz, przeanalizuj, dlaczego i spróbuj rozwiązać zadanie jeszcze raz.
Poproś o pomoc: Jeśli czegoś nie rozumiesz, nie wstydź się zapytać nauczyciela, rodziców, starszego rodzeństwa, kolegów. Wspólna nauka może być bardzo efektywna.
Ucz się regularnie: Nie zostawiaj nauki na ostatnią chwilę. Lepiej uczyć się po trochu każdego dnia, niż próbować "wkuć" wszystko w jeden wieczór.
Odpocznij: Przed sprawdzianem dobrze się wyśpij i zjedz śniadanie. Wypoczęty umysł lepiej pracuje!

Nie panikuj! Stres może utrudnić rozwiązywanie zadań. Spróbuj się zrelaksować i uwierz w siebie!

Counterpoint: "Ułamki są bez sensu!"

Słyszę czasem, że niektórzy uczniowie uważają ułamki za zbędne i nieprzydatne. Twierdzą, że to tylko skomplikowana teoria, która nie ma nic wspólnego z rzeczywistością. Rozumiem to poczucie. Jednak, jak pokazałem wcześniej, ułamki są obecne w wielu aspektach naszego życia. Co więcej, zrozumienie ułamków jest fundamentem dla bardziej zaawansowanych zagadnień matematycznych, takich jak algebra, geometria i trygonometria. Rezygnując z nauki ułamków, zamykasz sobie drogę do dalszego rozwoju.

Nawet jeśli nie planujesz zostać matematykiem, umiejętność operowania ułamkami będzie przydatna w wielu zawodach, np. w kuchni, budownictwie, finansach.

Błędy, których warto unikać

Zapominanie o sprowadzaniu do wspólnego mianownika: To kluczowy błąd przy dodawaniu i odejmowaniu ułamków o różnych mianownikach.
Błędne skracanie i rozszerzanie: Upewnij się, że dzielisz lub mnożysz zarówno licznik, jak i mianownik przez tę samą liczbę.
Zapominanie o odwrotności przy dzieleniu: Pamiętaj, żeby pomnożyć przez odwrotność drugiego ułamka, a nie dzielić bezpośrednio.
Błędy w mnożeniu i dzieleniu liczb mieszanych: Zamień liczbę mieszaną na ułamek niewłaściwy przed wykonaniem działania.
Niedokładne przepisywanie liczb: Zwracaj uwagę na szczegóły. Jedna źle przepisana cyfra może zepsuć całe rozwiązanie.

Rozwiązanie problemów z ułamkami

Jeśli masz trudności z ułamkami, nie poddawaj się! Oto kilka sposobów, aby je przezwyciężyć:

Skup się na podstawach: Upewnij się, że rozumiesz definicje i zasady. Wróć do wcześniejszych lekcji, jeśli to konieczne.
Użyj wizualizacji: Narysuj ułamki, podziel koło lub kwadrat na części. To pomoże Ci zrozumieć, co oznaczają ułamki.
Korzystaj z kalkulatora ułamkowego: To narzędzie może pomóc Ci sprawdzić swoje obliczenia i zidentyfikować błędy. Jednak nie polegaj na nim całkowicie. Ważne jest, aby umieć wykonywać działania na ułamkach samodzielnie.
Znajdź dobrego korepetytora: Korepetytor może pomóc Ci zrozumieć trudne zagadnienia i dostosować metody nauczania do Twoich indywidualnych potrzeb.
Bądź cierpliwy: Nauka ułamków wymaga czasu i wysiłku. Nie zniechęcaj się, jeśli nie od razu wszystko rozumiesz. Z czasem i praktyką, ułamki staną się dla Ciebie coraz łatwiejsze.

Pamiętaj! Każdy uczeń uczy się w swoim własnym tempie. Nie porównuj się z innymi. Skoncentruj się na swoich postępach i świętuj swoje sukcesy.

Wierzę w Ciebie! Przygotowując się solidnie, na pewno dasz sobie radę na sprawdzianie z ułamków. Powodzenia!

A teraz, co zamierzasz zrobić, żeby poczuć się pewniej przed jutrzejszym sprawdzianem? Może rozwiążesz jeszcze kilka zadań, a może poprosisz kogoś o pomoc? Wybór należy do Ciebie!