Ile Osi Symetrii Ma Prostokąt

Czy kiedykolwiek zastanawialiście się, dlaczego niektóre kształty wydają się nam bardziej harmonijne i przyjemne dla oka niż inne? Jednym z kluczy do tej harmonii jest symetria. W tym artykule przyjrzymy się bliżej, jak symetria manifestuje się w prostokącie i dlaczego jest to tak ważna cecha w matematyce, architekturze i naszym codziennym życiu. Artykuł ten jest skierowany do wszystkich, którzy chcą lepiej zrozumieć podstawowe pojęcia geometrii i dostrzec piękno ukryte w prostych kształtach.

Co to jest oś symetrii?

Zanim przejdziemy do prostokąta, zdefiniujmy, czym jest oś symetrii. Oś symetrii to linia, która dzieli figurę na dwie identyczne części, które są swoimi wzajemnymi odbiciami lustrzanymi. Innymi słowy, jeśli złożymy figurę wzdłuż osi symetrii, obie połówki powinny się idealnie pokryć.

Przykłady osi symetrii

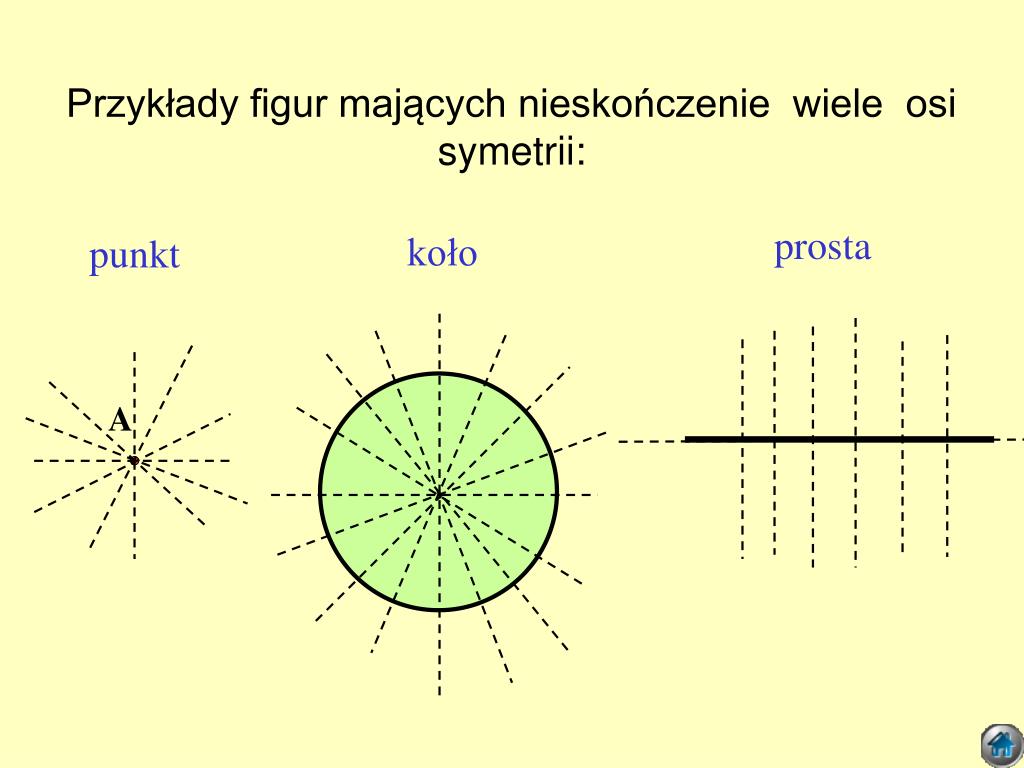
Okrąg: Ma nieskończenie wiele osi symetrii - każda linia przechodząca przez jego środek jest osią symetrii.
Kwadrat: Ma cztery osie symetrii - dwie przechodzące przez środki przeciwległych boków i dwie przechodzące przez przeciwległe wierzchołki.
Trójkąt równoboczny: Ma trzy osie symetrii - każda przechodzi przez wierzchołek i środek przeciwległego boku.

Ile osi symetrii ma prostokąt?

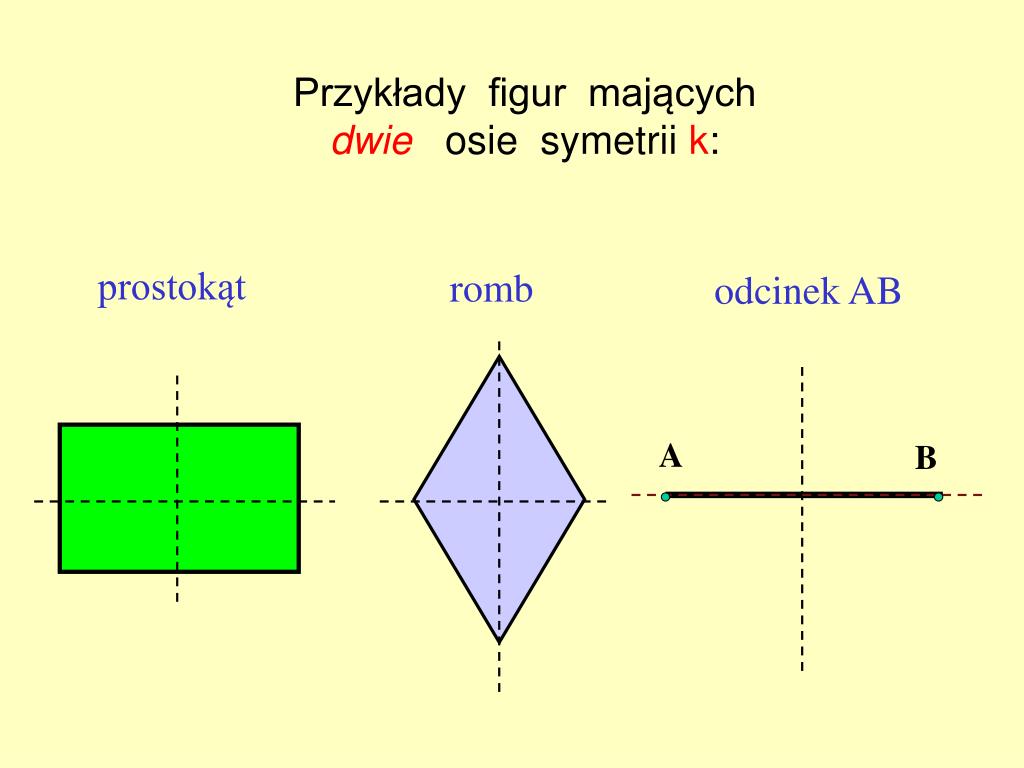
Prostokąt, choć wydaje się prostym kształtem, kryje w sobie pewną subtelność, jeśli chodzi o symetrię. Odpowiedź na pytanie, ile osi symetrii ma prostokąt, brzmi: dwa. Te dwie osie symetrii przechodzą przez środki przeciwległych boków prostokąta.

Wyjaśnienie

Spróbujmy zrozumieć, dlaczego tak jest. Wyobraźmy sobie prostokąt ABCD, gdzie AB i CD to dłuższe boki, a BC i AD to krótsze boki.

Pierwsza oś symetrii: Przechodzi przez środek boku AB i środek boku CD. Jeśli złożymy prostokąt wzdłuż tej osi, boki AD i BC idealnie się pokryją, a także połówki boków AB i CD.
Druga oś symetrii: Przechodzi przez środek boku BC i środek boku AD. Jeśli złożymy prostokąt wzdłuż tej osi, boki AB i CD idealnie się pokryją, a także połówki boków BC i AD.

Dlaczego linie przechodzące przez wierzchołki nie są osiami symetrii? Złożenie prostokąta wzdłuż takiej linii nie spowoduje, że połówki się pokryją. Jedna połówka będzie "wystawać" poza drugą, co dowodzi, że ta linia nie jest osią symetrii.

Dlaczego symetria jest ważna?

Symetria, w tym symetria osiowa, odgrywa kluczową rolę w wielu dziedzinach naszego życia:

Matematyka: Symetria jest fundamentalnym pojęciem w geometrii, algebrze i innych dziedzinach matematyki. Pomaga w rozwiązywaniu problemów i zrozumieniu relacji przestrzennych.
Architektura: Architekci od wieków wykorzystują symetrię, aby tworzyć budynki, które są estetyczne, stabilne i funkcjonalne. Symetria nadaje budynkom poczucie porządku i równowagi. Spójrzcie na fasady klasycznych budowli – często są symetryczne.
Sztuka: Wielu artystów używa symetrii, aby tworzyć dzieła, które są przyjemne dla oka i budzą poczucie harmonii. Symetria może być używana do tworzenia wzorów, kompozycji i układów, które są zarówno piękne, jak i efektywne.
Natura: Symetria występuje powszechnie w naturze, od płatków śniegu po liście drzew i ciała zwierząt. Ta symetria często odzwierciedla efektywność ewolucyjną i adaptację do środowiska.
Technologia: Symetria jest wykorzystywana w projektowaniu maszyn, urządzeń i systemów, aby zapewnić ich stabilność, wydajność i łatwość obsługi.

Prostokąt a inne czworokąty

Warto porównać prostokąt z innymi czworokątami pod względem osi symetrii:

Kwadrat: Jak wspomniano, ma cztery osie symetrii. Jest to szczególny przypadek prostokąta, w którym wszystkie boki są równe.
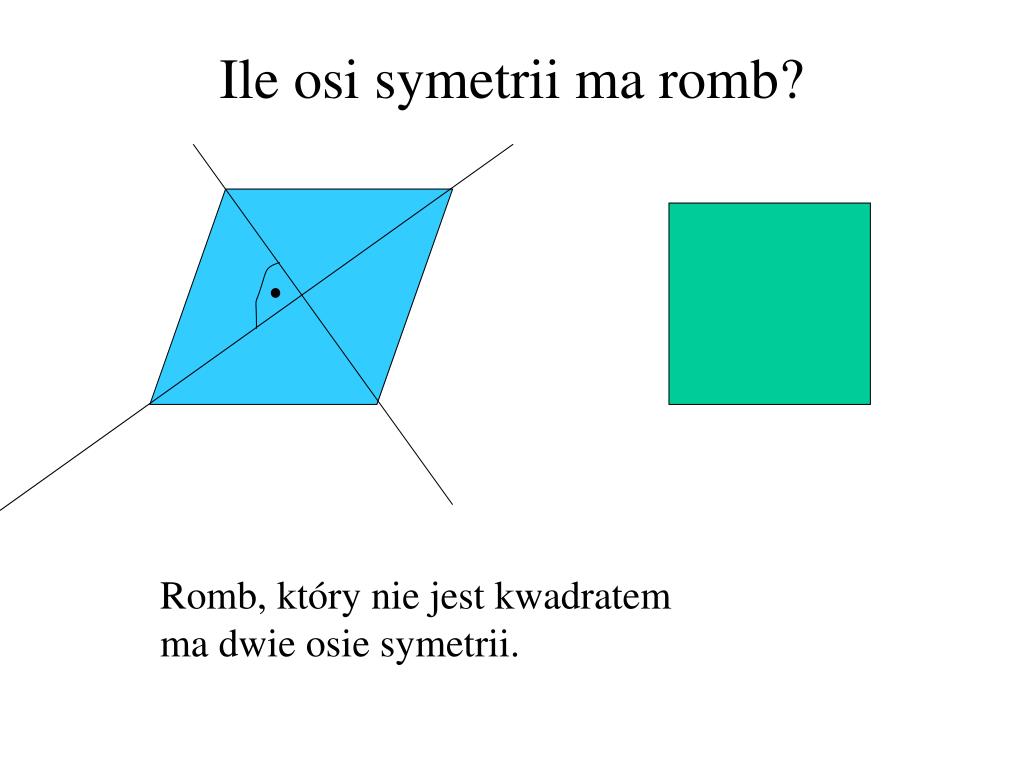
Romb: Ma dwie osie symetrii, które przechodzą przez jego wierzchołki.
Równoległobok: W ogólnym przypadku nie ma osi symetrii. Specjalny przypadek, prostokąt, już omówiliśmy.
Trapez równoramienny: Ma jedną oś symetrii, która przechodzi przez środki jego podstaw.
Trapez: W ogólnym przypadku nie ma osi symetrii.
Deltoid: Ma jedną oś symetrii, która przechodzi przez dwa przeciwległe wierzchołki.

Jak dostrzegać symetrię w codziennym życiu?

Symetria otacza nas z każdej strony. Ćwicząc swoje oko, możemy zacząć dostrzegać ją w wielu aspektach naszego otoczenia:

Budynki: Zwróć uwagę na fasady budynków, okna, drzwi i inne elementy architektoniczne.
Przedmioty codziennego użytku: Przyjrzyj się meblom, naczyniom, samochodom i innym przedmiotom.
Natura: Spójrz na liście, kwiaty, motyle i inne formy naturalne.
Sztuka i design: Zwróć uwagę na wzory na tkaninach, tapetach i innych elementach dekoracyjnych.

Ćwiczenie: Znajdź osie symetrii

Weź kartkę papieru i narysuj kilka prostokątów o różnych proporcjach. Spróbuj narysować osie symetrii dla każdego z nich. Możesz również wydrukować zdjęcia różnych przedmiotów i spróbować zidentyfikować ich osie symetrii.

Podsumowanie

Mam nadzieję, że ten artykuł pomógł Wam zrozumieć, ile osi symetrii ma prostokąt i dlaczego symetria jest tak ważna. Pamiętajcie, że prostokąt ma dwie osie symetrii, które przechodzą przez środki jego przeciwległych boków. Rozpoznawanie i docenianie symetrii w naszym otoczeniu może wzbogacić nasze postrzeganie świata i pomóc nam lepiej zrozumieć jego zasady. Dzięki znajomości symetrii możemy tworzyć lepsze projekty, budynki i dzieła sztuki. A przede wszystkim, możemy lepiej docenić piękno i harmonię, które nas otaczają. Zachęcam do dalszego zgłębiania wiedzy o geometrii i odkrywania piękna ukrytego w kształtach!

Pamiętajcie, że geometria nie jest tylko abstrakcyjną dziedziną matematyki. To język, którym opisuje się świat wokół nas. Zrozumienie tego języka pozwala nam lepiej rozumieć i doceniać piękno i harmonię, które nas otaczają.