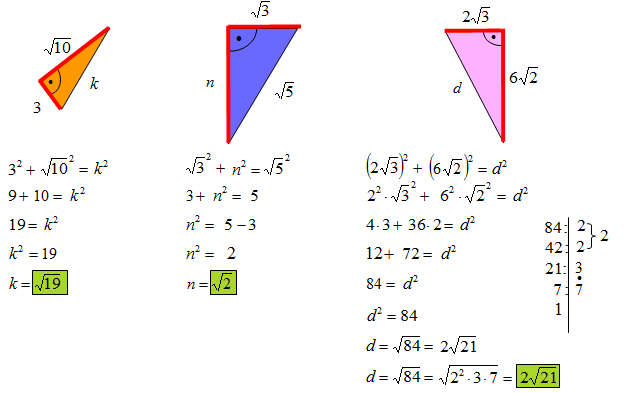Twierdzenie Pitagorasa Sprawdzian Klasa 8

Zbliża się sprawdzian z Twierdzenia Pitagorasa w klasie 8? Rozumiem Twój stres! Matematyka potrafi być wyzwaniem, szczególnie gdy w grę wchodzą nowe definicje, wzory i zadania, które na pierwszy rzut oka wydają się niemożliwe do rozwiązania. Ale spokojnie, ten artykuł ma Ci pomóc! Zamiast wkuwać regułki na pamięć, spróbujemy zrozumieć, o co tak naprawdę chodzi w tym słynnym twierdzeniu i jak go używać w praktyce. Razem przejdziemy przez najważniejsze aspekty, od podstaw po trudniejsze zadania, a także omówimy typowe błędy i jak ich unikać. Pamiętaj, sukces na sprawdzianie to nie tylko ocena, ale przede wszystkim satysfakcja z tego, że rozumiesz matematykę!

Co to jest Twierdzenie Pitagorasa?

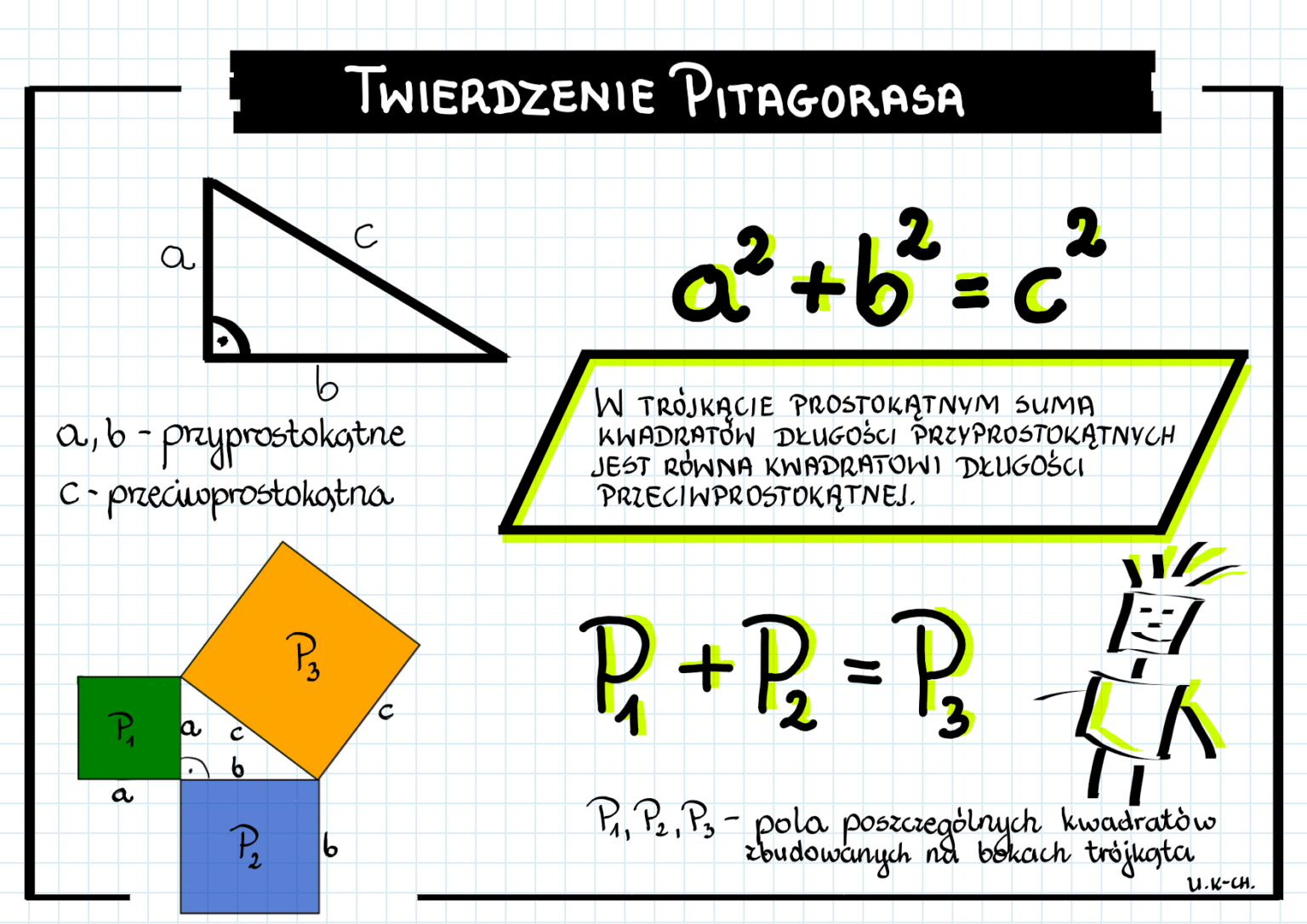
Twierdzenie Pitagorasa opisuje fundamentalną zależność między bokami trójkąta prostokątnego. Ale co to tak naprawdę znaczy? Wyobraź sobie trójkąt, który ma jeden kąt prosty (czyli taki, który wygląda jak róg kartki). Boki przylegające do tego kąta nazywamy przyprostokątnymi (oznaczmy je jako 'a' i 'b'), a bok naprzeciwko kąta prostego to przeciwprostokątna (oznaczmy ją jako 'c'). Twierdzenie Pitagorasa mówi, że:

a² + b² = c²

Prościej mówiąc: suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.

Analogia: Wyobraź sobie, że masz dwa kwadraty, jeden o boku 'a', a drugi o boku 'b'. Jeśli poskładasz ich pola w taki sposób, żeby stworzyć nowy kwadrat, to bok tego nowego kwadratu będzie miał długość 'c' (przeciwprostokątną).

Dlaczego to jest ważne?

Możesz pomyśleć: "Po co mi to w życiu?". Otóż, Twierdzenie Pitagorasa ma zastosowanie w wielu dziedzinach, od budownictwa po nawigację. Oto kilka przykładów:

• Budownictwo: Sprawdzanie, czy ściany są prostopadłe, obliczanie długości krokwi dachowych.
• Nawigacja: Określanie odległości i kierunków.
• Informatyka: Obliczanie odległości między punktami na ekranie.
• Geodezja: Wyznaczanie powierzchni działek.

To tylko kilka przykładów, a zastosowań jest o wiele więcej. Zrozumienie Twierdzenia Pitagorasa to klucz do rozwiązywania wielu problemów praktycznych.

Jak rozwiązywać zadania z Twierdzeniem Pitagorasa?

Najważniejsze to zrozumieć, co masz dane i czego szukasz. Poniżej przedstawiam kilka kroków, które pomogą Ci rozwiązać większość zadań:

1. Zidentyfikuj trójkąt prostokątny: Upewnij się, że w zadaniu występuje trójkąt prostokątny. Jeśli nie, Twierdzenie Pitagorasa nie zadziała.
2. Oznacz boki: Przyprostokątne oznacz jako 'a' i 'b', a przeciwprostokątną jako 'c'.
3. Zapisz wzór: Napisz wzór Twierdzenia Pitagorasa: a² + b² = c².
4. Podstaw dane: Wstaw znane wartości do wzoru.
5. Rozwiąż równanie: Oblicz nieznaną wartość. Pamiętaj o pierwiastkowaniu, jeśli szukasz długości boku, a masz jego kwadrat.
6. Sprawdź wynik: Upewnij się, że wynik ma sens. Długość boku nie może być ujemna, a przeciwprostokątna musi być najdłuższa.

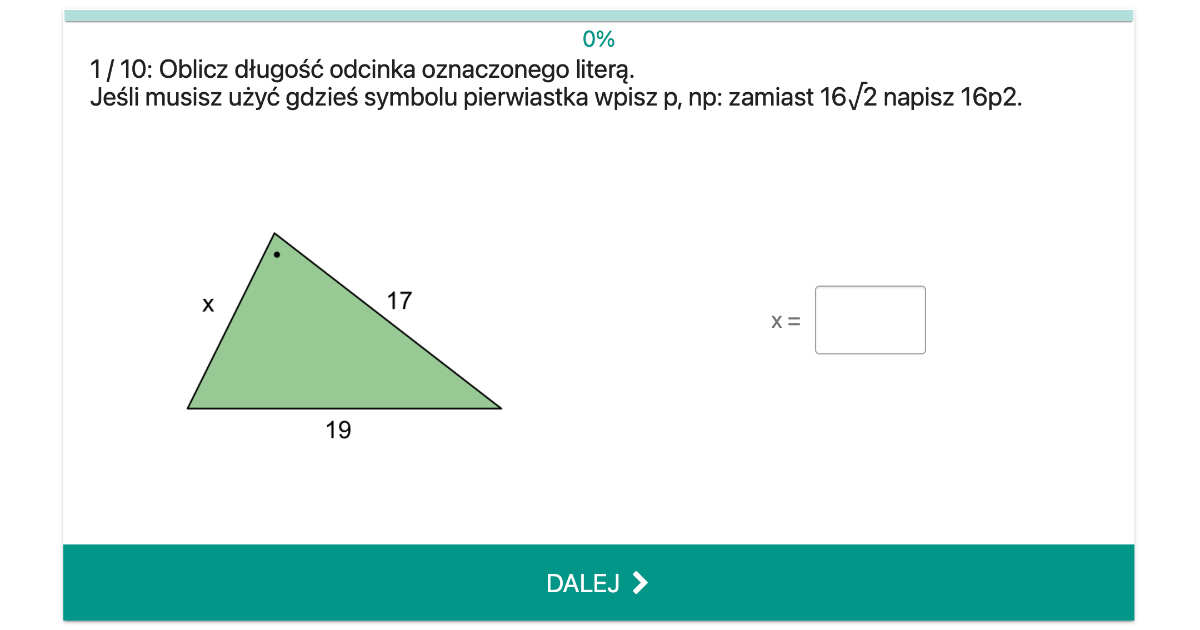
Przykładowe zadania:

Zadanie 1: Przyprostokątne trójkąta prostokątnego mają długości 3 cm i 4 cm. Oblicz długość przeciwprostokątnej.

Rozwiązanie:

1. Mamy trójkąt prostokątny.
2. a = 3 cm, b = 4 cm, c = ?
3. a² + b² = c²
4. 3² + 4² = c²
5. 9 + 16 = c²
   25 = c²
   c = √25 = 5 cm
6. Długość przeciwprostokątnej wynosi 5 cm.

Zadanie 2: Przeciwprostokątna trójkąta prostokątnego ma długość 13 cm, a jedna z przyprostokątnych ma długość 5 cm. Oblicz długość drugiej przyprostokątnej.

Rozwiązanie:

1. Mamy trójkąt prostokątny.
2. a = 5 cm, b = ?, c = 13 cm
3. a² + b² = c²
4. 5² + b² = 13²
5. 25 + b² = 169
   b² = 169 - 25
   b² = 144
   b = √144 = 12 cm
6. Długość drugiej przyprostokątnej wynosi 12 cm.

Typowe błędy i jak ich unikać

Podczas rozwiązywania zadań z Twierdzeniem Pitagorasa łatwo o pomyłkę. Oto kilka najczęstszych błędów i wskazówki, jak ich unikać:

• Pomylenie boków: Upewnij się, że poprawnie zidentyfikowałeś przyprostokątne i przeciwprostokątną. Najczęstszy błąd to wstawienie złej wartości do wzoru.
• Zapominanie o kwadratach: Pamiętaj, że wzór dotyczy kwadratów długości boków, a nie samych długości.
• Błędy w obliczeniach: Uważaj na błędy w dodawaniu, odejmowaniu, mnożeniu i pierwiastkowaniu. Sprawdź swoje obliczenia, a najlepiej użyj kalkulatora.
• Zapominanie o jednostkach: Zawsze podawaj jednostki w odpowiedzi (np. cm, m, km).
• Stosowanie Twierdzenia Pitagorasa do trójkątów innych niż prostokątne: Twierdzenie Pitagorasa działa tylko dla trójkątów prostokątnych. Jeśli trójkąt nie jest prostokątny, musisz użyć innych metod (np. twierdzenia cosinusów).

Trójki Pitagorejskie

Trójki Pitagorejskie to zestawy trzech liczb naturalnych, które spełniają Twierdzenie Pitagorasa (a² + b² = c²). Znajomość kilku podstawowych trójek może znacznie przyspieszyć rozwiązywanie zadań.

Oto kilka najpopularniejszych trójek Pitagorejskich:

• 3, 4, 5 (3² + 4² = 5²)
• 5, 12, 13 (5² + 12² = 13²)
• 8, 15, 17 (8² + 15² = 17²)
• 7, 24, 25 (7² + 24² = 25²)

Co ważne, każda wielokrotność trójki Pitagorejskiej również jest trójką Pitagorejską. Na przykład, 6, 8, 10 (2 * 3, 2 * 4, 2 * 5) to również trójka Pitagorejska.

Twierdzenie Pitagorasa w układzie współrzędnych

Twierdzenie Pitagorasa można wykorzystać do obliczania odległości między dwoma punktami w układzie współrzędnych. Załóżmy, że mamy dwa punkty: A(x₁, y₁) i B(x₂, y₂). Odległość między nimi (d) można obliczyć ze wzoru:

d = √((x₂ - x₁)² + (y₂ - y₁)²)

Ten wzór jest po prostu aplikacją Twierdzenia Pitagorasa do trójkąta prostokątnego, którego boki są równoległe do osi układu współrzędnych, a przeciwprostokątna łączy punkty A i B.

Przeciwdowody i ograniczenia

Chociaż Twierdzenie Pitagorasa jest fundamentalne i powszechnie stosowane, warto zauważyć, że ma ono swoje ograniczenia. Nie stosuje się go bezpośrednio do trójkątów, które nie są prostokątne. W takich przypadkach konieczne jest użycie bardziej ogólnych twierdzeń, takich jak twierdzenie cosinusów lub twierdzenie sinusów. Ponadto, w geometriach nieeuklidesowych, które badają zakrzywione przestrzenie, relacje między bokami trójkątów mogą być inne niż te opisane przez Twierdzenie Pitagorasa.

Podsumowanie i wskazówki na sprawdzian

Przygotowanie do sprawdzianu z Twierdzenia Pitagorasa to przede wszystkim zrozumienie jego istoty i umiejętność stosowania go w praktyce. Pamiętaj o:

• Zrozumieniu wzoru: a² + b² = c²
• Identyfikowaniu przyprostokątnych i przeciwprostokątnej.
• Uważaniu na jednostki.
• Sprawdzaniu wyników.
• Znajomości podstawowych trójek Pitagorejskich.
• Umiejętności zastosowania Twierdzenia Pitagorasa w układzie współrzędnych.

Przede wszystkim, nie panikuj! Wykonaj kilka zadań treningowych, powtórz definicje i wzory, a na pewno dasz radę! Powodzenia!

Teraz, zastanów się: jakie zadanie z Twierdzeniem Pitagorasa sprawia Ci najwięcej trudności? Spróbuj je rozwiązać ponownie, krok po kroku, i przeanalizuj, gdzie popełniałeś błędy. Czy widzisz teraz to zadanie inaczej?