Trójkat 90 60 30 Stopni

Zastanawiałeś się kiedyś, jak potężna może być geometria, a konkretnie – trójkąt prostokątny o kątach 90, 60 i 30 stopni? Może aktualnie zmagasz się z zadaniem z matematyki, może projektujesz konstrukcję i potrzebujesz precyzyjnych obliczeń, a może po prostu fascynuje Cię świat kształtów i ich zależności. Niezależnie od powodu, chcę Ci pokazać, dlaczego ten konkretny trójkąt zasługuje na szczególną uwagę i jak jego właściwości mogą Ci się przydać w wielu sytuacjach.

Dlaczego trójkąt 30-60-90 jest wyjątkowy?

Trójkąt prostokątny o kątach 30, 60 i 90 stopni to specyficzny przypadek trójkąta prostokątnego, który charakteryzuje się bardzo prostymi i eleganckimi zależnościami między długościami boków. Te zależności wynikają bezpośrednio z geometrii, a ich znajomość znacząco ułatwia rozwiązywanie wielu problemów.

Podstawowe zależności

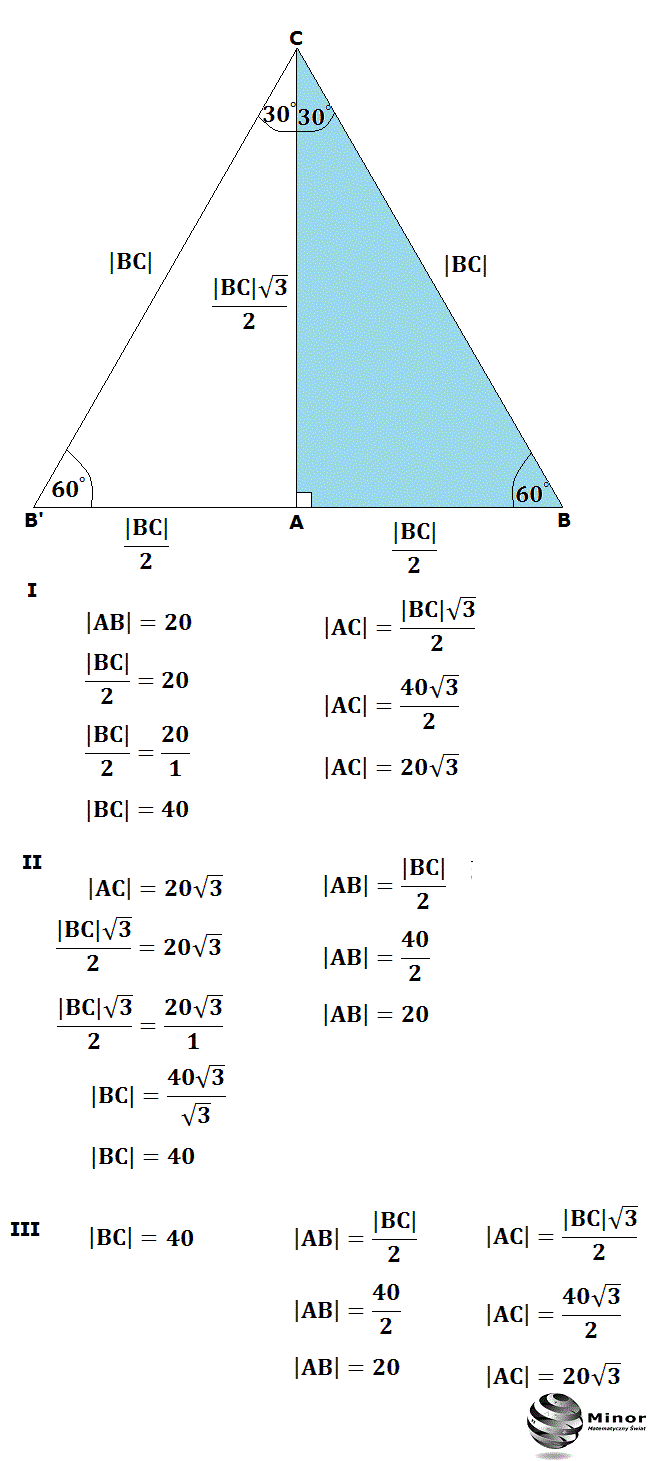
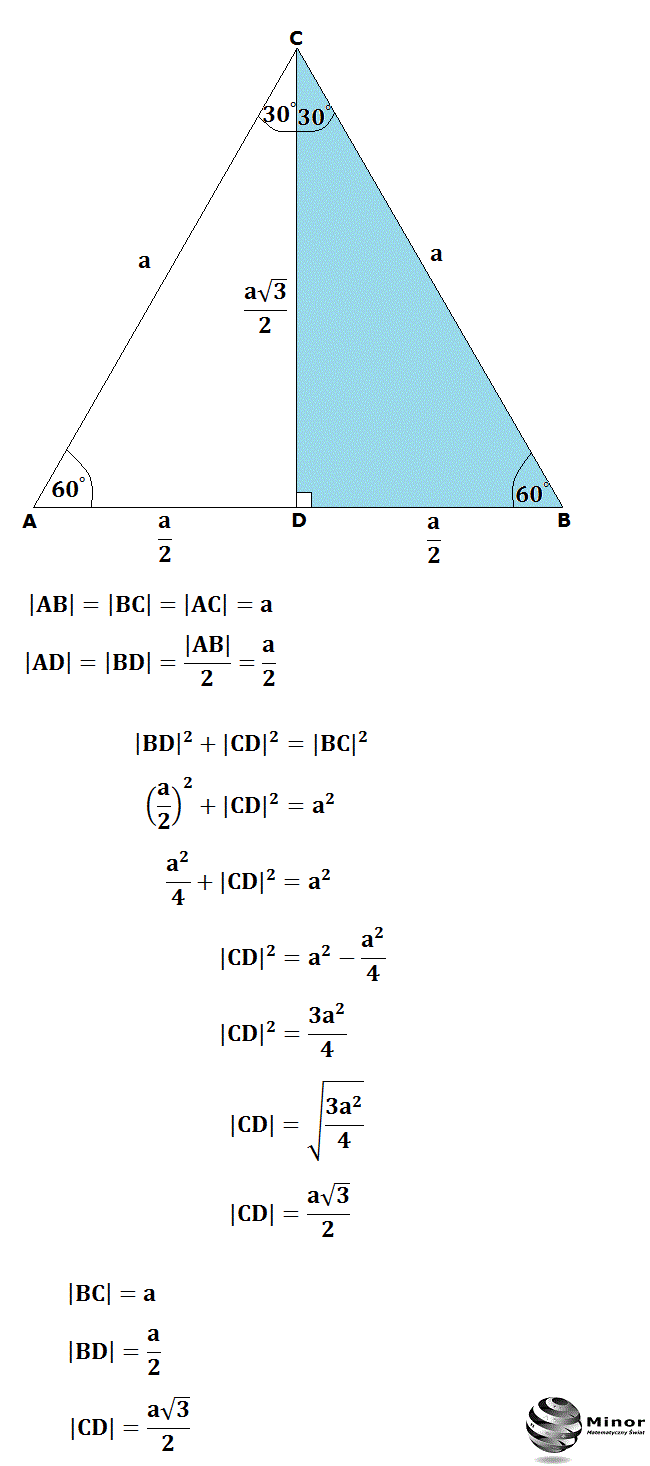
Kluczową cechą tego trójkąta jest proporcja między długościami jego boków. Oznaczmy:

Najkrótszy bok (naprzeciwko kąta 30 stopni) jako a
Bok średniej długości (naprzeciwko kąta 60 stopni) jako b
Przeciwprostokątną (naprzeciwko kąta 90 stopni) jako c

Wtedy zachodzą następujące zależności:

c = 2a (Przeciwprostokątna jest dwa razy dłuższa od najkrótszego boku)
b = a√3 (Bok średniej długości jest √3 razy dłuższy od najkrótszego boku)

Te proste wzory pozwalają na szybkie wyznaczenie długości pozostałych boków, znając długość tylko jednego z nich. To ogromne ułatwienie w wielu sytuacjach praktycznych.

Praktyczne zastosowania trójkąta 30-60-90

Wbrew pozorom, trójkąt 30-60-90 nie jest jedynie abstrakcyjnym tworem matematycznym. Jego właściwości znajdują szerokie zastosowanie w wielu dziedzinach.

Architektura i budownictwo

W architekturze i budownictwie precyzja jest kluczowa. Trójkąt 30-60-90 często pojawia się w projektowaniu dachów, schodów, a także przy konstruowaniu różnych elementów dekoracyjnych. Znając kąty i proporcje, architekci i inżynierowie mogą dokładnie obliczyć wymiary poszczególnych elementów, co przekłada się na stabilność i estetykę konstrukcji.

Na przykład, budując dach o kącie nachylenia 30 stopni, możemy łatwo obliczyć wysokość szczytu dachu, znając długość jego podstawy. To znacznie upraszcza proces projektowania i minimalizuje ryzyko błędów.

Inżynieria

W inżynierii trójkąt 30-60-90 jest nieoceniony przy rozwiązywaniu problemów związanych z siłami i momentami. Analizując konstrukcje narażone na obciążenia, inżynierowie często rozkładają siły na składowe pionowe i poziome. Kąty 30 i 60 stopni ułatwiają te obliczenia, pozwalając na szybkie i precyzyjne określenie wartości poszczególnych składowych.

Wyobraź sobie dźwig podnoszący ciężar. Za pomocą trójkąta 30-60-90 możemy łatwo obliczyć siłę potrzebną do utrzymania ładunku w równowadze, biorąc pod uwagę kąt nachylenia liny.

Nawigacja i geodezja

W nawigacji i geodezji trójkąt 30-60-90 wykorzystywany jest do obliczania odległości i wysokości. Na przykład, mierząc kąt pod jakim widać wierzchołek góry i znając odległość od punktu pomiaru do podstawy góry, możemy obliczyć wysokość góry za pomocą zależności trygonometrycznych, które upraszczają się dzięki znajomości kątów 30, 60 i 90 stopni.

Dodatkowo, w geodezji, przy tworzeniu map i planów, trójkąt 30-60-90 pomaga w precyzyjnym wyznaczaniu położenia punktów w przestrzeni.

Grafika komputerowa i gry

W grafice komputerowej i tworzeniu gier trójkąty, w tym trójkąt 30-60-90, są podstawowym elementem konstrukcyjnym. Wykorzystywane są do modelowania obiektów, obliczania perspektywy i tworzenia realistycznych animacji. Znajomość proporcji boków trójkąta 30-60-90 ułatwia tworzenie precyzyjnych modeli 3D i optymalizację kodu.

Na przykład, projektując budynek w grze, możemy szybko obliczyć wymiary poszczególnych elementów konstrukcyjnych, wykorzystując właściwości trójkąta 30-60-90.

Adresowanie potencjalnych kontrargumentów

Można usłyszeć argument, że w dzisiejszych czasach, z dostępem do zaawansowanych narzędzi obliczeniowych, znajomość właściwości trójkąta 30-60-90 nie jest już tak istotna. Rzeczywiście, programy komputerowe i kalkulatory mogą szybko rozwiązać skomplikowane zadania. Jednak zrozumienie podstawowych zasad geometrii, w tym właściwości trójkąta 30-60-90, pozwala na lepsze zrozumienie wyników obliczeń i unikanie błędów. Narzędzia są pomocne, ale to wiedza pozwala na krytyczną ocenę ich wyników.

Ponadto, w sytuacjach, gdy nie mamy dostępu do komputera lub kalkulatora (na przykład w terenie, podczas projektowania na kartce papieru), znajomość właściwości trójkąta 30-60-90 może okazać się nieoceniona.

Jak wykorzystać tę wiedzę?

Oto kilka praktycznych wskazówek, jak możesz wykorzystać wiedzę o trójkącie 30-60-90:

Ćwicz rozwiązywanie zadań: Im więcej zadań rozwiążesz, tym lepiej utrwalisz wiedzę i nauczysz się rozpoznawać sytuacje, w których możesz wykorzystać właściwości trójkąta 30-60-90.
Szukaj trójkątów 30-60-90 w otoczeniu: Zwracaj uwagę na konstrukcje architektoniczne, elementy krajobrazu, a nawet przedmioty codziennego użytku. Zauważanie występowania tego trójkąta w realnym świecie pomoże Ci lepiej zrozumieć jego znaczenie.
Używaj narzędzi online: Istnieje wiele darmowych narzędzi online, które pozwalają na wizualizację trójkątów i eksperymentowanie z ich właściwościami.
Dziel się wiedzą z innymi: Wyjaśniaj innym, jak działa trójkąt 30-60-90. Uczenie innych utrwala Twoją wiedzę i pozwala na spojrzenie na temat z nowej perspektywy.

Podsumowanie

Trójkąt prostokątny o kątach 30, 60 i 90 stopni to potężne narzędzie, które znajduje szerokie zastosowanie w wielu dziedzinach. Znajomość jego właściwości ułatwia rozwiązywanie problemów w architekturze, inżynierii, nawigacji, grafice komputerowej i wielu innych obszarach. Nawet w dobie zaawansowanych technologii, zrozumienie podstawowych zasad geometrii pozostaje kluczowe dla efektywnego rozwiązywania problemów i podejmowania świadomych decyzji.

Mam nadzieję, że ten artykuł przybliżył Ci temat trójkąta 30-60-90 i zainspirował do dalszego zgłębiania wiedzy z zakresu geometrii. Pamiętaj, że matematyka to nie tylko zbiór wzorów, ale przede wszystkim narzędzie, które pozwala nam lepiej zrozumieć świat wokół nas.

Teraz Twoja kolej. Jak możesz wykorzystać wiedzę o trójkącie 30-60-90 w swoim życiu lub pracy?