Zadania Z Obliczania Pola Figur

Czy kiedykolwiek zastanawiałeś się, jak obliczyć ilość farby potrzebnej do pomalowania ściany, albo ile materiału zużyjesz na uszycie obrusu? Odpowiedź kryje się w **obliczaniu pola figur geometrycznych**! Ten artykuł jest dla Ciebie, jeśli chcesz odświeżyć swoją wiedzę z geometrii, przygotowujesz się do egzaminu, albo po prostu jesteś ciekawy, jak matematyka pomaga nam w życiu codziennym. Zapraszamy do wspólnej podróży po świecie figur i ich pól!

Wprowadzenie do obliczania pola figur

Pole figury geometrycznej to miara powierzchni, jaką ta figura zajmuje na płaszczyźnie. Wyrażamy ją zazwyczaj w jednostkach kwadratowych, takich jak centymetry kwadratowe (cm²), metry kwadratowe (m²), czy kilometry kwadratowe (km²). Znajomość metod obliczania pola jest niezbędna w wielu dziedzinach życia, od architektury i budownictwa, przez rolnictwo, po projektowanie wnętrz i grafikę komputerową.

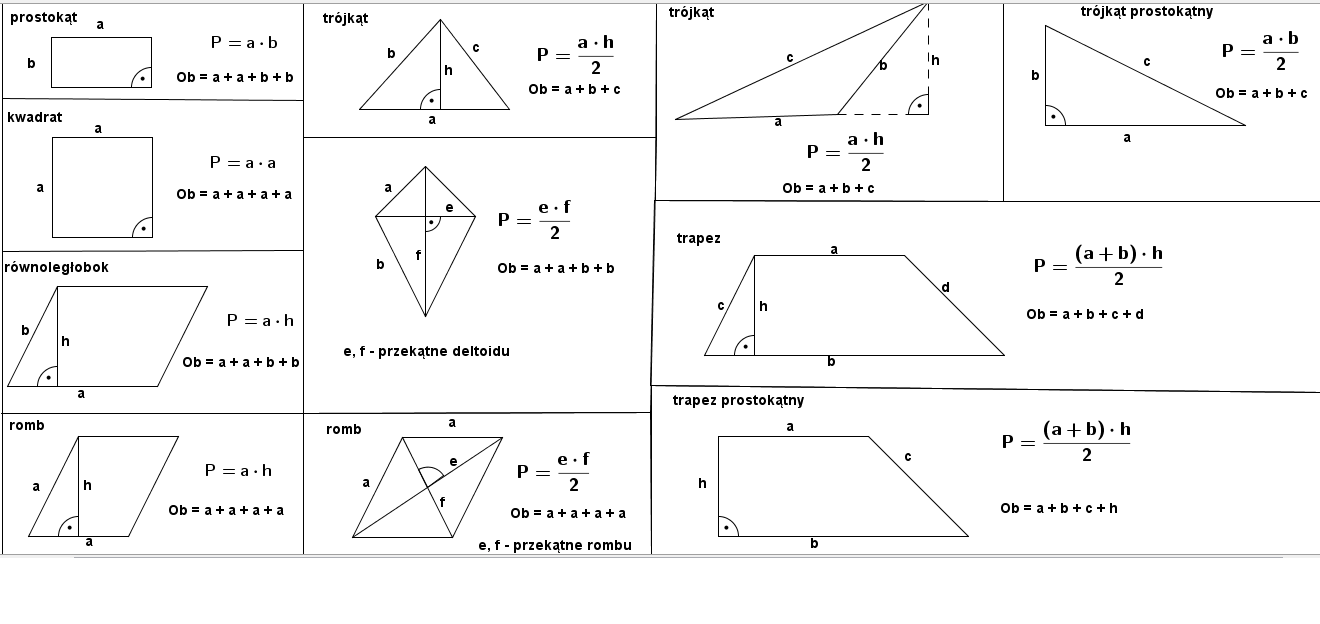
W tym artykule skupimy się na obliczaniu pola podstawowych figur geometrycznych, takich jak kwadrat, prostokąt, trójkąt, równoległobok, romb, trapez i koło. Przejdziemy przez wzory, przykłady i praktyczne zastosowania, aby każdy mógł z łatwością opanować tę umiejętność.

Podstawowe figury i ich pola

Kwadrat

Kwadrat to czworokąt, który ma wszystkie boki równe i wszystkie kąty proste. Jest to jedna z najprostszych figur geometrycznych, a obliczenie jego pola jest bardzo łatwe:

Wzór: Pole kwadratu (P) o boku długości 'a' wynosi: P = a²
Przykład: Jeśli bok kwadratu ma długość 5 cm, to jego pole wynosi: P = 5 cm * 5 cm = 25 cm²
Zastosowanie: Obliczanie powierzchni płytek podłogowych w kwadratowym pomieszczeniu.

Prostokąt

Prostokąt to czworokąt, który ma wszystkie kąty proste, ale niekoniecznie wszystkie boki równe. Ma dwie pary boków o równej długości.

Wzór: Pole prostokąta (P) o bokach długości 'a' i 'b' wynosi: P = a * b
Przykład: Jeśli boki prostokąta mają długości 8 cm i 3 cm, to jego pole wynosi: P = 8 cm * 3 cm = 24 cm²
Zastosowanie: Obliczanie powierzchni ekranu telewizora, powierzchni dywanu, czy powierzchni działki.

Trójkąt

Trójkąt to figura geometryczna, która ma trzy boki i trzy kąty. Istnieje wiele rodzajów trójkątów, ale najprostszy wzór na pole dotyczy trójkąta o znanej podstawie i wysokości.

Wzór: Pole trójkąta (P) o podstawie 'a' i wysokości 'h' opuszczonej na tę podstawę wynosi: P = (1/2) * a * h
Przykład: Jeśli podstawa trójkąta ma długość 10 cm, a wysokość opuszczona na tę podstawę ma długość 6 cm, to jego pole wynosi: P = (1/2) * 10 cm * 6 cm = 30 cm²
Zastosowanie: Obliczanie powierzchni żagla, powierzchni dachu w kształcie trójkąta, czy powierzchni rabaty kwiatowej.

Ważne! Wysokość trójkąta to odcinek prostopadły do podstawy, łączący ją z wierzchołkiem leżącym naprzeciwko tej podstawy.

Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Ważne jest, aby pamiętać, że kąty równoległoboku nie muszą być proste (w przeciwieństwie do prostokąta).

Wzór: Pole równoległoboku (P) o podstawie 'a' i wysokości 'h' opuszczonej na tę podstawę wynosi: P = a * h
Przykład: Jeśli podstawa równoległoboku ma długość 7 cm, a wysokość opuszczona na tę podstawę ma długość 4 cm, to jego pole wynosi: P = 7 cm * 4 cm = 28 cm²
Zastosowanie: Obliczanie powierzchni parkietu ułożonego w wzór równoległoboku.

Romb

Romb to równoległobok, który ma wszystkie boki równe. Jest szczególnym przypadkiem równoległoboku, gdzie wszystkie boki mają taką samą długość.

Wzór 1: Pole rombu (P) o podstawie 'a' i wysokości 'h' opuszczonej na tę podstawę wynosi: P = a * h (tak jak w równoległoboku)
Wzór 2: Pole rombu (P) o przekątnych 'd1' i 'd2' wynosi: P = (1/2) * d1 * d2
Przykład 1: Jeśli bok rombu ma długość 6 cm, a wysokość opuszczona na ten bok ma długość 5 cm, to jego pole wynosi: P = 6 cm * 5 cm = 30 cm²
Przykład 2: Jeśli przekątne rombu mają długości 8 cm i 10 cm, to jego pole wynosi: P = (1/2) * 8 cm * 10 cm = 40 cm²
Zastosowanie: Obliczanie powierzchni płytek w kształcie rombu, powierzchni latawca.

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Te boki równoległe nazywamy podstawami trapezu.

Wzór: Pole trapezu (P) o podstawach 'a' i 'b' oraz wysokości 'h' wynosi: P = (1/2) * (a + b) * h
Przykład: Jeśli podstawy trapezu mają długości 4 cm i 6 cm, a wysokość wynosi 3 cm, to jego pole wynosi: P = (1/2) * (4 cm + 6 cm) * 3 cm = 15 cm²
Zastosowanie: Obliczanie powierzchni dachu w kształcie trapezu, powierzchni pola.

Koło

Koło to zbiór wszystkich punktów na płaszczyźnie, które znajdują się w tej samej odległości od danego punktu, zwanego środkiem koła. Odległość od środka do dowolnego punktu na okręgu nazywamy promieniem (r).

Wzór: Pole koła (P) o promieniu 'r' wynosi: P = π * r² (gdzie π (pi) to stała matematyczna, w przybliżeniu równa 3.14159)
Przykład: Jeśli promień koła wynosi 5 cm, to jego pole wynosi: P = π * (5 cm)² ≈ 3.14159 * 25 cm² ≈ 78.54 cm²
Zastosowanie: Obliczanie powierzchni pizzy, powierzchni basenu o kształcie koła, powierzchni okrągłego stolika.

Praktyczne zastosowania obliczania pola figur

Jak już wspomnieliśmy, obliczanie pola figur ma ogromne znaczenie w wielu dziedzinach. Oto kilka przykładów:

Budownictwo i Architektura: Obliczanie powierzchni ścian, podłóg, dachów, potrzebne do oszacowania kosztów materiałów budowlanych, takich jak farba, płytki, czy panele podłogowe.
Rolnictwo: Obliczanie powierzchni pól uprawnych, potrzebne do planowania zasiewów, nawożenia, i szacowania plonów.
Projektowanie wnętrz: Obliczanie powierzchni ścian, podłóg, mebli, potrzebne do planowania rozmieszczenia mebli, doboru odpowiednich dywanów, czy tapet.
Grafika komputerowa: Obliczanie powierzchni obiektów graficznych, potrzebne do renderowania obrazów, tworzenia animacji, i projektowania gier.
Krawiectwo: Obliczanie powierzchni materiału potrzebnego do uszycia ubrań, zasłon, obrusów.

Wskazówki i triki

Oto kilka wskazówek, które mogą Ci pomóc w obliczaniu pola figur:

Zawsze zwracaj uwagę na jednostki! Upewnij się, że wszystkie wymiary są podane w tej samej jednostce (np. centymetry, metry). Jeśli nie są, przekształć je.
Narysuj schemat! Narysowanie schematu figury, którą masz obliczyć, może pomóc Ci zrozumieć problem i zidentyfikować odpowiednie wymiary.
Podziel złożone figury na prostsze! Jeśli masz do obliczenia pole figury o nieregularnym kształcie, spróbuj podzielić ją na mniejsze, prostsze figury (np. kwadraty, prostokąty, trójkąty), oblicz pole każdej z nich, a następnie zsumuj wyniki.
Korzystaj z kalkulatora! Nie krępuj się korzystać z kalkulatora, szczególnie przy obliczeniach z liczbami dziesiętnymi lub z liczbą π.

Podsumowanie

Obliczanie pola figur geometrycznych to umiejętność przydatna w życiu codziennym i wielu dziedzinach zawodowych. Mamy nadzieję, że ten artykuł pomógł Ci odświeżyć swoją wiedzę i zrozumieć, jak stosować wzory na pole w praktyce. Pamiętaj, że ćwiczenie czyni mistrza! Rozwiązuj zadania, analizuj przykłady, a z pewnością opanujesz tę umiejętność. Powodzenia!

Zachęcamy do dalszego zgłębiania wiedzy z geometrii i odkrywania fascynującego świata matematyki. Znajomość geometrii otwiera drzwi do lepszego zrozumienia świata, który nas otacza.