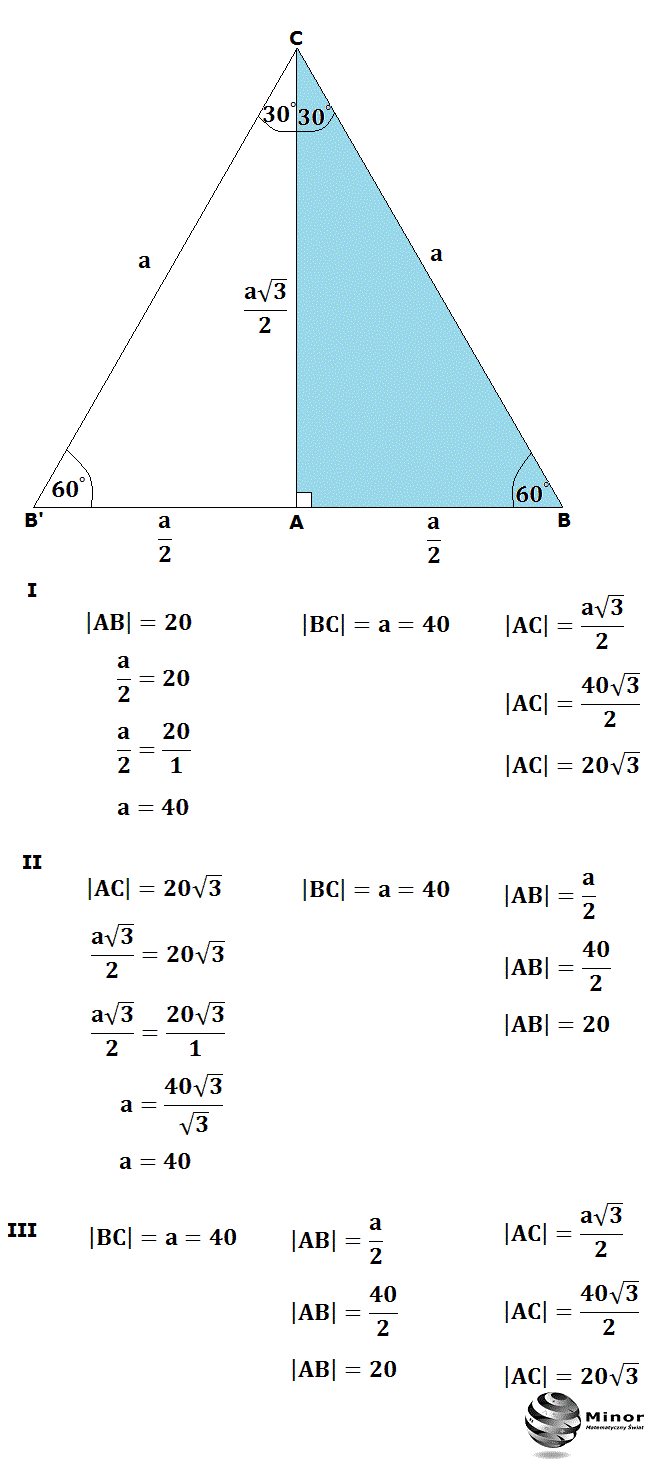Trójkat 30 60 90 Stopni

Czy kiedykolwiek zastanawiałeś się, jak niektóre rzeczy w matematyce wydają się być magicznie połączone? Jak z prostej figury geometrycznej, takiej jak trójkąt, można wywnioskować mnóstwo informacji bez konieczności mozolnych obliczeń? Jeśli tak, to artykuł ten jest dla Ciebie. Skupimy się na szczególnym rodzaju trójkąta prostokątnego – trójkącie o kątach 30, 60 i 90 stopni. Zrozumienie jego właściwości może znacznie ułatwić rozwiązywanie zadań z geometrii i trygonometrii, a nawet znaleźć zastosowanie w życiu codziennym.

Dlaczego trójkąt 30-60-90 jest tak ważny?

Trójkąt o kątach 30°, 60° i 90° to jeden z najbardziej fundamentalnych trójkątów w geometrii. Jego popularność wynika z prostych relacji między długościami jego boków. Znając długość tylko jednego boku, możemy bez problemu obliczyć długości pozostałych! To ogromne ułatwienie, szczególnie w zadaniach, gdzie inne metody obliczeniowe byłyby znacznie bardziej czasochłonne.

Podstawowe własności i zależności

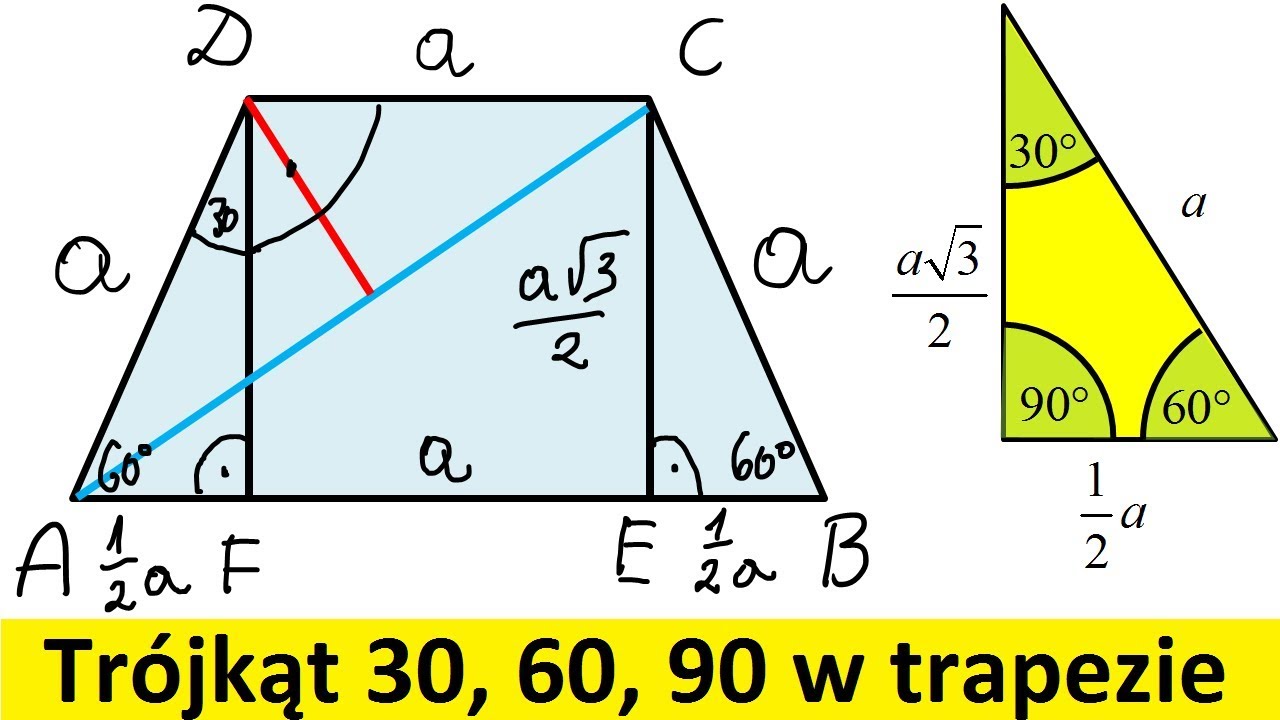
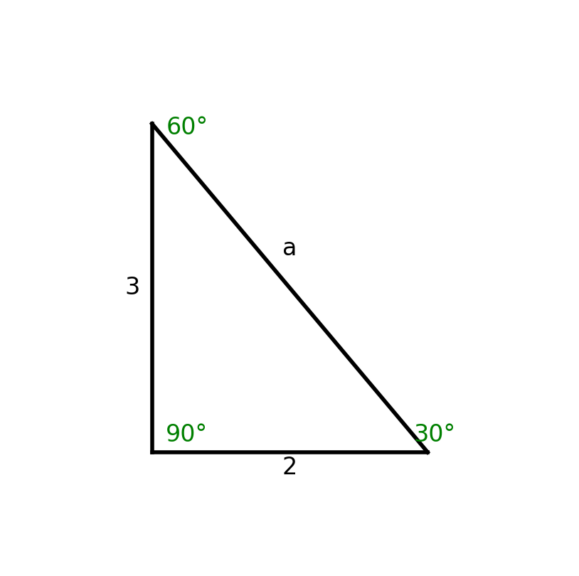
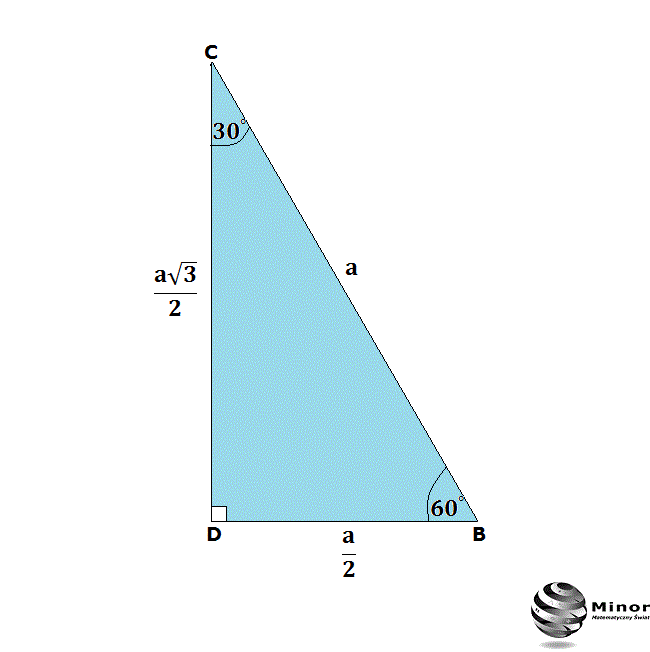
Kluczem do zrozumienia trójkąta 30-60-90 są relacje między jego bokami. Wyobraź sobie ten trójkąt. Najkrótszy bok leży naprzeciwko kąta 30 stopni. Oznaczmy jego długość jako a. Wtedy:

Bok naprzeciwko kąta 60 stopni (czyli dłuższa przyprostokątna) ma długość a√3.
Przeciwprostokątna (bok naprzeciwko kąta 90 stopni) ma długość 2a.

Te proste zależności stanowią podstawę wszystkich obliczeń związanych z tym trójkątem. Zwróć uwagę, że wszystkie boki są wprost proporcjonalne do siebie. To oznacza, że jeśli na przykład przeciwprostokątna ma długość 10, to najkrótszy bok ma długość 5 (10 / 2), a dłuższa przyprostokątna ma długość 5√3.

Skąd się biorą te zależności?

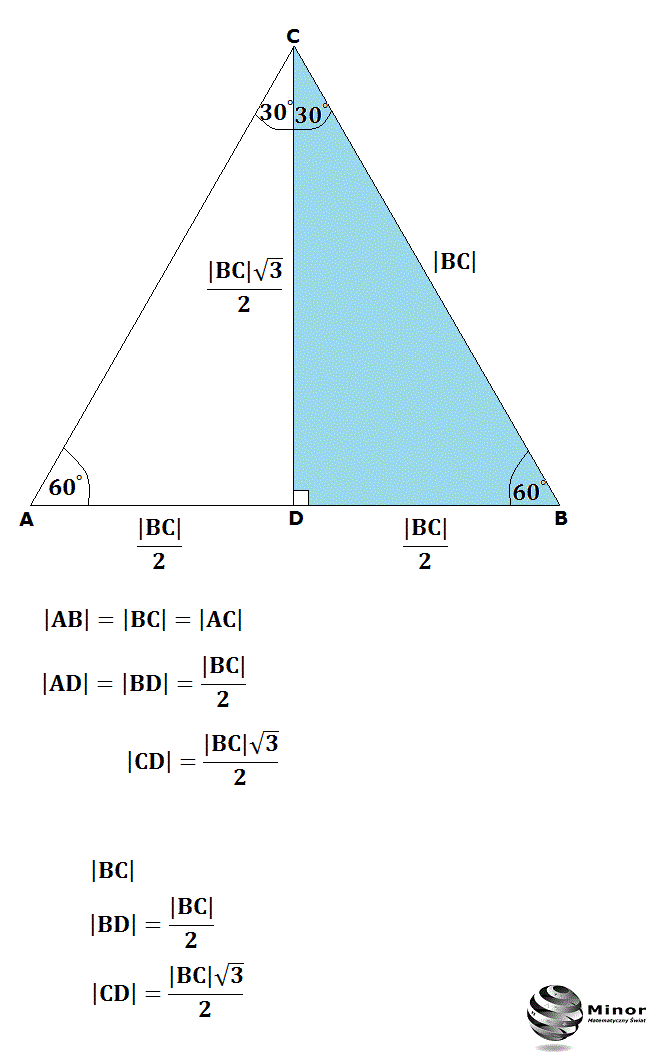
Te zależności wynikają bezpośrednio z własności trójkąta równobocznego. Wyobraź sobie trójkąt równoboczny. Wszystkie jego kąty mają 60 stopni, a wszystkie boki są równe. Jeśli przetniemy go na pół, prowadząc wysokość z jednego wierzchołka na przeciwległy bok, otrzymamy dwa identyczne trójkąty prostokątne o kątach 30, 60 i 90 stopni. Wysokość trójkąta równobocznego jest jednocześnie jego środkową, dlatego dzieli podstawę na dwie równe części. Dzięki temu możemy łatwo wyprowadzić wzory na długości boków trójkąta 30-60-90.

Możemy również wyprowadzić te zależności za pomocą funkcji trygonometrycznych, takich jak sinus i cosinus. Wiemy, że sin(30°) = 1/2, cos(30°) = √3/2, sin(60°) = √3/2, a cos(60°) = 1/2. Stosując te wartości do definicji sinusa i cosinusa w trójkącie prostokątnym, otrzymamy dokładnie te same relacje między bokami.

Praktyczne zastosowania

Trójkąt 30-60-90 nie jest tylko teoretycznym konceptem. Ma wiele praktycznych zastosowań w różnych dziedzinach.

Geometria i trygonometria

To chyba najbardziej oczywiste zastosowanie. Trójkąt 30-60-90 jest często wykorzystywany w zadaniach z geometrii i trygonometrii, szczególnie tych dotyczących obliczania pól i obwodów figur, znajdowania długości odcinków i kątów. Jego znajomość pozwala na szybkie rozwiązywanie wielu problemów bez konieczności używania skomplikowanych wzorów.

Na przykład, wyobraź sobie, że masz trójkąt równoboczny o boku długości 6. Chcesz obliczyć jego wysokość. Możesz podzielić ten trójkąt na dwa trójkąty 30-60-90. Wtedy najkrótszy bok jednego z tych trójkątów ma długość 3 (połowa boku trójkąta równobocznego). Wysokość trójkąta równobocznego, będąca jednocześnie dłuższą przyprostokątną trójkąta 30-60-90, ma długość 3√3.

Architektura i budownictwo

Trójkąty 30-60-90 znajdują zastosowanie w architekturze i budownictwie, szczególnie przy projektowaniu dachów, schodów i innych konstrukcji, gdzie ważna jest precyzja i stabilność. Znajomość relacji między bokami tego trójkąta pozwala na łatwe obliczanie wymiarów i kątów nachylenia.

Wyobraź sobie, że projektujesz dach. Chcesz, żeby kąt nachylenia dachu wynosił 30 stopni. Możesz użyć trójkąta 30-60-90, aby obliczyć długość krokwi i wysokość dachu, znając rozpiętość dachu.

Fizyka

W fizyce trójkąt 30-60-90 może być użyteczny przy rozkładaniu sił na składowe, analizie ruchu po równi pochyłej i innych zagadnieniach związanych z wektorami i geometrią.

Na przykład, jeśli ciało zsuwa się po równi pochyłej o kącie 30 stopni, możesz użyć trójkąta 30-60-90, aby rozłożyć siłę ciężkości na składową równoległą do równi pochyłej i składową prostopadłą do niej. To ułatwi obliczenie siły tarcia i przyspieszenia ciała.

Jak zapamiętać relacje między bokami?

Najlepszym sposobem na zapamiętanie relacji między bokami trójkąta 30-60-90 jest praktyka. Rozwiązuj zadania, rysuj trójkąty, eksperymentuj z różnymi wartościami długości boków. Im więcej ćwiczysz, tym łatwiej zapamiętasz te zależności.

Oto kilka dodatkowych wskazówek:

Wizualizacja: Wyobraź sobie trójkąt równoboczny przecięty na pół. To pomoże Ci zapamiętać, skąd biorą się te zależności.
Skojarzenia: Skojarz najkrótszy bok z kątem 30 stopni, a dłuższą przyprostokątną z kątem 60 stopni.
Używaj mnemotechnik: Stwórz własne rymowanki lub wierszyki, które pomogą Ci zapamiętać wzory.

Podsumowanie

Trójkąt 30-60-90 to potężne narzędzie w matematyce i nie tylko. Jego proste, ale zarazem fundamentalne własności pozwalają na szybkie i efektywne rozwiązywanie wielu problemów. Znajomość tego trójkąta jest nieoceniona w geometrii, trygonometrii, architekturze, budownictwie i fizyce. Poświęć trochę czasu na zrozumienie i zapamiętanie relacji między jego bokami, a z pewnością zauważysz, jak wiele zadań stanie się prostszych i bardziej intuicyjnych.

Pamiętaj, praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym pewniej będziesz się czuł w posługiwaniu się tym trójkątem. Nie zrażaj się początkowymi trudnościami. Z czasem zrozumienie i intuicja przyjdą same.

Odkryj magię trójkąta 30-60-90 i wykorzystaj jego potencjał! Powodzenia!