Kola I Okregi Klasa 8

Hej! Zastanawiasz się, co to w ogóle są Koła i Okręgi w 8 klasie? Może wydają Ci się trudne i abstrakcyjne? Bez obaw! W tym artykule postaramy się krok po kroku wyjaśnić wszystko, co musisz wiedzieć o tej części geometrii, tak aby stała się ona dla Ciebie zrozumiała i nawet... interesująca! Skupimy się na tym, by teoria przełożyła się na praktykę, a Ty byłeś w stanie rozwiązać każde zadanie.

Czym są Koła i Okręgi? Podstawowe definicje

Zacznijmy od absolutnych podstaw. To fundament, na którym budujemy całą naszą wiedzę.

• Okrąg: To zbiór wszystkich punktów na płaszczyźnie, które znajdują się w dokładnie takiej samej odległości od jednego ustalonego punktu, zwanego środkiem okręgu. Wyobraź sobie, że wbijaasz cyrkiel w kartkę i rysujesz nim linię – to właśnie jest okrąg.
• Koło: To zbiór wszystkich punktów na płaszczyźnie, które znajdują się w odległości mniejszej lub równej odległości od ustalonego punktu, zwanego środkiem koła. Koło to okrąg wraz z całym obszarem wewnątrz niego. Pomyśl o pizzy – cała pizza to koło, a jej brzeg to okrąg.
• Środek okręgu/koła (O): Punkt, od którego wszystkie punkty na okręgu/w kole są jednakowo oddalone.
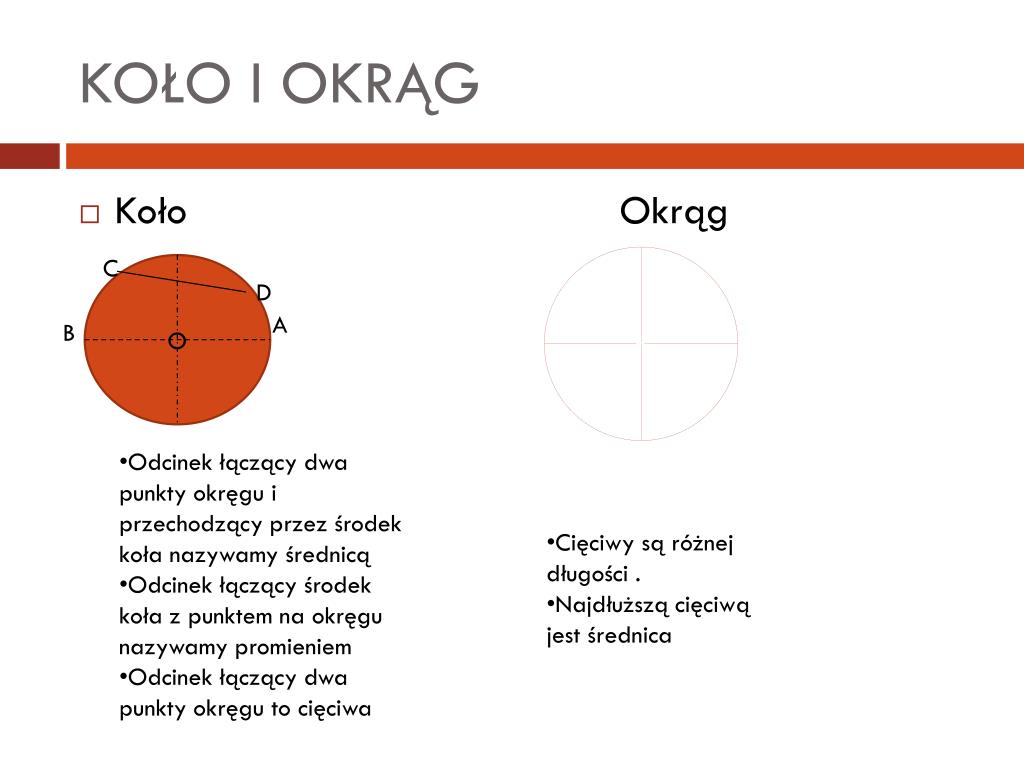
• Promień (r): Odcinek łączący środek okręgu/koła z dowolnym punktem na okręgu. Wszystkie promienie danego okręgu/koła mają tę samą długość.
• Średnica (d): Odcinek przechodzący przez środek okręgu/koła i łączący dwa punkty na okręgu. Średnica jest dwa razy dłuższa od promienia (d = 2r).
• Cięciwa: Odcinek łączący dwa dowolne punkty na okręgu. Średnica jest najdłuższą cięciwą.

Pamiętaj: Okrąg to tylko linia! Koło to obszar ograniczony okręgiem!

Długość Okręgu i Pole Koła

Teraz, gdy już znamy podstawy, możemy przejść do obliczania ważnych parametrów.

Długość okręgu (obwód)

Długość okręgu, nazywana również jego obwodem, możemy obliczyć za pomocą następującego wzoru:

L = 2πr

Gdzie:

• L - długość okręgu
• π (pi) - stała matematyczna, w przybliżeniu równa 3,14
• r - promień okręgu

Możemy również użyć średnicy do obliczenia długości okręgu:

L = πd

Gdzie:

• d - średnica okręgu

Przykład: Okrąg ma promień równy 5 cm. Oblicz jego długość.

Rozwiązanie: L = 2πr = 2 * 3,14 * 5 cm = 31,4 cm

Pole koła

Pole koła obliczamy za pomocą następującego wzoru:

P = πr²

Gdzie:

• P - pole koła
• π (pi) - stała matematyczna, w przybliżeniu równa 3,14
• r - promień koła

Przykład: Koło ma promień równy 4 cm. Oblicz jego pole.

Rozwiązanie: P = πr² = 3,14 * (4 cm)² = 3,14 * 16 cm² = 50,24 cm²

Wzajemne położenie okręgów

Dwa okręgi mogą względem siebie znajdować się w różny sposób. Ważne jest, aby umieć rozpoznać i nazwać te położenia. Rozpatrujemy to w zależności od odległości między ich środkami (oznaczmy ją jako |OO'|) oraz długości ich promieni (r i r').

• Okręgi rozłączne zewnętrznie: Odległość między środkami okręgów jest większa niż suma ich promieni. |OO'| > r + r'
• Okręgi styczne zewnętrznie: Odległość między środkami okręgów jest równa sumie ich promieni. |OO'| = r + r'
• Okręgi przecinające się: Odległość między środkami okręgów jest mniejsza niż suma ich promieni i większa niż różnica ich promieni. |r - r'| < |OO'| < r + r'
• Okręgi styczne wewnętrznie: Odległość między środkami okręgów jest równa różnicy ich promieni. |OO'| = |r - r'| (gdzie r > r')
• Okręgi rozłączne wewnętrznie: Odległość między środkami okręgów jest mniejsza niż różnica ich promieni. |OO'| < |r - r'| (gdzie r > r')
• Okręgi współśrodkowe (koncentryczne): Okręgi mają ten sam środek. |OO'| = 0

Spróbuj narysować sobie każdy z tych przypadków! To bardzo pomaga w zapamiętaniu.

Kąty w okręgu

W okręgu możemy wyróżnić dwa ważne rodzaje kątów: kąt środkowy i kąt wpisany.

Kąt środkowy

Kąt środkowy to kąt, którego wierzchołek znajduje się w środku okręgu, a ramiona przecinają okrąg. Miarę kąta środkowego mierzymy w stopniach.

Ważne: Miara kąta środkowego jest równa mierze łuku, na którym jest oparty.

Kąt wpisany

Kąt wpisany to kąt, którego wierzchołek znajduje się na okręgu, a ramiona przecinają okrąg.

Ważne: Miara kąta wpisanego jest równa połowie miary kąta środkowego opartego na tym samym łuku.

Konsekwencja: Wszystkie kąty wpisane oparte na tym samym łuku mają tę samą miarę.

Konsekwencja: Kąt wpisany oparty na średnicy jest kątem prostym (ma miarę 90°).

Okrąg opisany na trójkącie

Mówimy, że okrąg jest opisany na trójkącie, jeśli wszystkie wierzchołki trójkąta leżą na okręgu.

Twierdzenie: Na każdym trójkącie można opisać okrąg. Środek okręgu opisanego na trójkącie leży w punkcie przecięcia się symetralnych boków tego trójkąta.

Ciekawostka: Dla trójkąta prostokątnego środek okręgu opisanego leży w środku przeciwprostokątnej.

Okrąg wpisany w trójkąt

Mówimy, że okrąg jest wpisany w trójkąt, jeśli okrąg jest styczny do każdego z boków trójkąta.

Twierdzenie: W każdy trójkąt można wpisać okrąg. Środek okręgu wpisanego w trójkąt leży w punkcie przecięcia się dwusiecznych kątów tego trójkąta.

Zastosowanie w zadaniach

Teraz przejdźmy do tego, co najważniejsze – jak tę wiedzę wykorzystać w praktyce? Oto kilka wskazówek i typowych zadań:

• Obliczanie długości okręgu i pola koła: Zadania polegają na podstawieniu danych do wzoru i obliczeniu wyniku. Czasami trzeba najpierw obliczyć promień lub średnicę. Uważaj na jednostki!
• Określanie wzajemnego położenia okręgów: Trzeba obliczyć odległość między środkami okręgów i porównać ją z sumą/różnicą promieni.
• Obliczanie miar kątów w okręgu: Korzystamy z zależności między kątami środkowymi i wpisanymi. Często trzeba zauważyć, że kąt jest oparty na średnicy (czyli jest prosty).
• Zadania z okręgami opisanymi i wpisanymi: Trzeba wykorzystać właściwości symetralnych boków i dwusiecznych kątów. Przydatne jest też twierdzenie o kącie wpisanym opartym na średnicy.
• Zadania tekstowe: Tutaj kluczem jest uważne czytanie i wyciągnięcie z treści wszystkich istotnych informacji. Spróbuj narysować rysunek pomocniczy!

Przykład zadania: Dwa okręgi o promieniach 3 cm i 5 cm są styczne zewnętrznie. Oblicz odległość między ich środkami.

Rozwiązanie: Ponieważ okręgi są styczne zewnętrznie, odległość między ich środkami jest równa sumie ich promieni. Czyli odległość wynosi 3 cm + 5 cm = 8 cm.

Jak się uczyć?

Geometria wymaga ćwiczeń, ćwiczeń i jeszcze raz ćwiczeń! Oto kilka porad:

• Rozwiązuj dużo zadań: Im więcej zadań zrobisz, tym lepiej zrozumiesz teorię i nauczysz się schematów rozwiązywania.
• Rób rysunki: Rysunek pomocniczy to połowa sukcesu! Pomaga zrozumieć treść zadania i dostrzec zależności.
• Ucz się na błędach: Nie zrażaj się, jeśli popełniasz błędy. Analizuj je i staraj się zrozumieć, dlaczego się pomyliłeś.
• Korzystaj z różnych źródeł: Oprócz podręcznika, korzystaj z internetu, zbiorów zadań, a także z pomocy nauczyciela lub kolegów.
• Wyjaśniaj innym: Jeśli potrafisz komuś wytłumaczyć dane zagadnienie, to znaczy, że naprawdę je rozumiesz.
• Ucz się regularnie: Nie zostawiaj nauki na ostatnią chwilę. Lepiej uczyć się systematycznie, po trochu każdego dnia.

Podsumowanie

Koła i okręgi w 8 klasie to ważny temat, który wymaga zrozumienia podstawowych definicji, wzorów i zależności. Pamiętaj, że kluczem do sukcesu jest systematyczna nauka i rozwiązywanie dużej liczby zadań. Nie bój się pytać i szukać pomocy, jeśli czegoś nie rozumiesz. Wierzymy w Ciebie! Powodzenia!

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć temat kół i okręgów. Teraz śmiało możesz sięgać po kolejne zadania i doskonalić swoje umiejętności. Pamiętaj, że geometria to nie tylko wzory i twierdzenia, ale także logiczne myślenie i kreatywność. Baw się dobrze!