Znajdz Dwie Kolejne Liczby Calkowite Miedzy Ktorymi

Hej Studenci! Witajcie! Dzisiaj przygotujemy się do rozwiązywania problemów typu "Znajdź Dwie Kolejne Liczby Całkowite Między Którymi...". To może brzmieć skomplikowanie, ale obiecuję, że po tym artykule, będziecie się czuli pewni siebie i gotowi na każde zadanie tego typu. Będziemy pracować krok po kroku, tłumacząc wszystko jasno i przejrzyście. Nie ma co się bać, matematyka może być fajna! Skupmy się, a na pewno dasz radę!

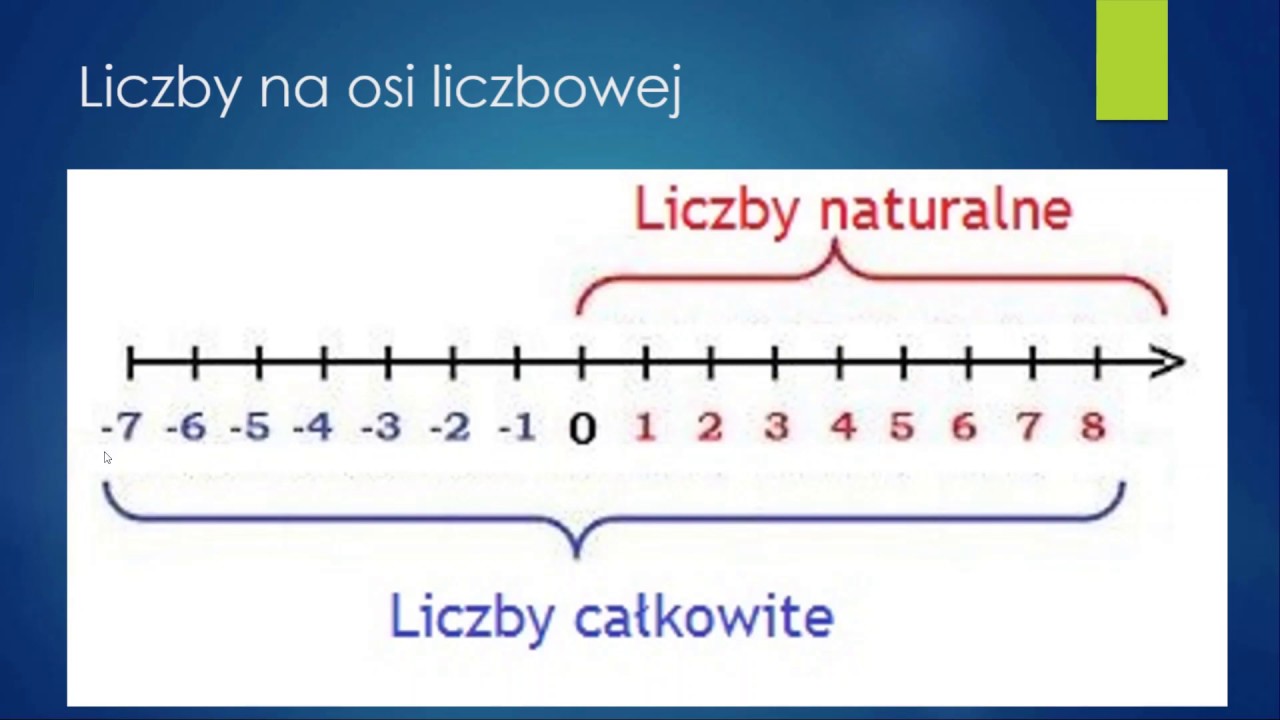
1. Co to są Liczby Całkowite i Liczby Kolejne?

Zacznijmy od podstaw. Liczby całkowite to wszystkie liczby bez części ułamkowych i dziesiętnych. Obejmują liczby dodatnie (1, 2, 3...), liczby ujemne (-1, -2, -3...) oraz zero (0). Liczby całkowite nie obejmują takich wartości jak 1.5, -2.7 czy √2. Pamiętajcie o tym dobrze!

Teraz liczby kolejne. To liczby, które następują po sobie w porządku rosnącym, z różnicą równą 1. Przykłady liczb kolejnych to:

• 1 i 2
• 5 i 6
• -3 i -2
• 100 i 101

Kluczowe jest zrozumienie, że między dwiema kolejnymi liczbami całkowitymi nie ma innych liczb całkowitych. To bardzo ważne dla rozwiązywania zadań.

2. Jak Rozwiązać Zadanie typu "Znajdź Dwie Kolejne Liczby Całkowite..."?

Zazwyczaj zadania tego typu będą dotyczyć pierwiastków kwadratowych lub innych wyrażeń, które nie dają w wyniku liczby całkowitej. Na przykład, zadanie może brzmieć: "Znajdź dwie kolejne liczby całkowite, między którymi znajduje się √17."

Oto krok po kroku, jak rozwiązać takie zadanie:

Krok 1: Oszacuj wartość wyrażenia.

Najważniejszym krokiem jest oszacowanie wartości, o której mowa w zadaniu. W naszym przykładzie to √17. Zastanów się, jakie kwadraty liczb całkowitych są blisko 17.

• Wiemy, że 4² = 16
• I że 5² = 25

Zauważamy, że 17 leży pomiędzy 16 a 25. To oznacza, że √17 leży pomiędzy √16 a √25.

Krok 2: Wyciągnij pierwiastki z najbliższych kwadratów.

Skoro √17 leży pomiędzy √16 a √25, to możemy wyciągnąć pierwiastki:

• √16 = 4
• √25 = 5

Krok 3: Wyciągnij wniosek.

Teraz wiemy, że √17 leży pomiędzy 4 a 5. Zatem, odpowiedź na pytanie "Znajdź dwie kolejne liczby całkowite, między którymi znajduje się √17" to: 4 i 5.

3. Przykłady Rozwiązywania Zadań

Przeanalizujmy kilka przykładów, żeby jeszcze lepiej zrozumieć ten proces.

Przykład 1:

Znajdź dwie kolejne liczby całkowite, między którymi znajduje się √30.

• Krok 1: Szukamy najbliższych kwadratów liczb całkowitych do 30. Wiemy, że 5² = 25, a 6² = 36. 30 leży pomiędzy 25 a 36.
• Krok 2: Wyciągamy pierwiastki: √25 = 5, √36 = 6.
• Krok 3: Wniosek: √30 leży pomiędzy 5 a 6. Odpowiedź: 5 i 6.

Przykład 2:

Znajdź dwie kolejne liczby całkowite, między którymi znajduje się √68.

• Krok 1: Szukamy najbliższych kwadratów liczb całkowitych do 68. Wiemy, że 8² = 64, a 9² = 81. 68 leży pomiędzy 64 a 81.
• Krok 2: Wyciągamy pierwiastki: √64 = 8, √81 = 9.
• Krok 3: Wniosek: √68 leży pomiędzy 8 a 9. Odpowiedź: 8 i 9.

Przykład 3:

Znajdź dwie kolejne liczby całkowite, między którymi znajduje się √110.

• Krok 1: Szukamy najbliższych kwadratów liczb całkowitych do 110. Wiemy, że 10² = 100, a 11² = 121. 110 leży pomiędzy 100 a 121.
• Krok 2: Wyciągamy pierwiastki: √100 = 10, √121 = 11.
• Krok 3: Wniosek: √110 leży pomiędzy 10 a 11. Odpowiedź: 10 i 11.

Przykład 4 (Trochę trudniejszy):

Znajdź dwie kolejne liczby całkowite, między którymi znajduje się ∛30 (pierwiastek sześcienny z 30).

• Krok 1: Tutaj szukamy najbliższych sześcianów liczb całkowitych do 30. Wiemy, że 3³ = 27, a 4³ = 64. 30 leży pomiędzy 27 a 64.
• Krok 2: Wyciągamy pierwiastki sześcienne: ∛27 = 3, ∛64 = 4.
• Krok 3: Wniosek: ∛30 leży pomiędzy 3 a 4. Odpowiedź: 3 i 4.

Pamiętajcie, że czasami zadanie może dotyczyć pierwiastków wyższego stopnia niż kwadratowe. Ważne jest, żeby znać potęgi kilku pierwszych liczb naturalnych.

4. Kilka Wskazówek i Triki

• Zapamiętaj kwadraty i sześciany: Pomocne jest zapamiętanie kwadratów liczb od 1 do 15 (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225) oraz sześcianów liczb od 1 do 5 (1, 8, 27, 64, 125). To znacznie przyspieszy szacowanie.
• Używaj kalkulatora (jeśli możesz): Jeśli masz dostęp do kalkulatora, możesz użyć go do przybliżonego obliczenia wartości wyrażenia. To pomoże Ci szybko zorientować się, między jakimi liczbami całkowitymi leży wynik. Pamiętaj jednak, że sam kalkulator nie da Ci rozwiązania – musisz nadal rozumieć, jak interpretować wynik.
• Sprawdź odpowiedź: Po znalezieniu dwóch liczb, możesz szybko sprawdzić, czy Twoja odpowiedź ma sens. Na przykład, jeśli masz √20, wiesz, że powinno to być coś pomiędzy √16 (czyli 4) a √25 (czyli 5). Jeśli obliczenia dały Ci liczby 6 i 7, wiesz, że gdzieś popełniłeś błąd.
• Ćwicz, ćwicz, ćwicz!: Najlepszym sposobem na opanowanie tej umiejętności jest rozwiązywanie jak największej liczby zadań. Im więcej ćwiczysz, tym szybciej i pewniej będziesz w stanie znajdować poprawne odpowiedzi.

Podsumowanie

• Liczby całkowite: Liczby bez części ułamkowych i dziesiętnych (…, -2, -1, 0, 1, 2, …).
• Liczby kolejne: Liczby następujące po sobie w porządku rosnącym, z różnicą równą 1.
• Metoda rozwiązywania:
  1. Oszacuj wartość wyrażenia (np. √17).
  2. Znajdź najbliższe kwadraty (lub sześciany, itp.) liczb całkowitych.
  3. Wyciągnij pierwiastki.
  4. Wyciągnij wniosek i podaj dwie kolejne liczby całkowite.
• Wskazówki: Zapamiętaj kwadraty i sześciany, używaj kalkulatora (jeśli możesz), sprawdzaj odpowiedź, ćwicz regularnie.

Pamiętajcie, że matematyka to umiejętność, którą można rozwijać. Nie zniechęcajcie się, jeśli na początku coś wydaje się trudne. Z odrobiną wysiłku i systematycznej pracy, na pewno poradzicie sobie z każdym zadaniem! Trzymam za was kciuki i życzę powodzenia na egzaminie!