Zastosowanie Matematyki Klasa 8 Gwo

Drodzy nauczyciele Matematyki w klasie 8, witajcie! Ten artykuł ma na celu pomóc Wam w efektywnym nauczaniu zagadnienia Zastosowania Matematyki zgodnie z programem GWO. Zrozumienie praktycznego wymiaru matematyki jest kluczowe dla rozwoju umiejętności uczniów i ich motywacji do dalszej nauki. Przyjrzyjmy się bliżej temu zagadnieniu, omówmy typowe trudności oraz strategie, które pomogą Wam uczynić te lekcje fascynującymi.

Dlaczego Zastosowania Matematyki są Ważne?

Zastosowania Matematyki w klasie 8 to nie tylko powtórka znanych wzorów i twierdzeń. To przede wszystkim pokazanie uczniom, jak wiedza teoretyczna przekłada się na realne sytuacje. Dzięki temu:

Uczniowie widzą sens uczenia się matematyki, co zwiększa ich motywację.
Rozwijają umiejętność rozwiązywania problemów.
Uczą się modelowania matematycznego – przekształcania rzeczywistych sytuacji na język matematyki.
Przygotowują się do dalszej edukacji i życia zawodowego, gdzie umiejętności matematyczne są niezbędne.

Kluczowe Zagadnienia w Zastosowaniach Matematyki GWO (Klasa 8)

Program GWO zazwyczaj obejmuje następujące obszary zastosowań matematyki w klasie 8. Ważne jest, aby upewnić się, że pokrywasz wszystkie punkty z aktualnego programu nauczania. Poniżej znajdują się ogólne przykłady:

1. Procenty w praktyce

Obliczanie procentów jest niezwykle przydatne w życiu codziennym. Uczniowie powinni rozumieć, jak obliczać:

Podwyżki i obniżki cen.
Rabaty i marże.
Procent składany (np. przy lokatach bankowych).
Zawartość procentową w roztworach i mieszaninach.

Jak uczyć? Wykorzystajcie konkretne przykłady z życia – promocje w sklepach, kredyty bankowe, kalkulacje związane z finansami osobistymi. Można nawet zorganizować symulację zakupów, gdzie uczniowie będą obliczać ceny po rabatach i z podatkiem VAT.

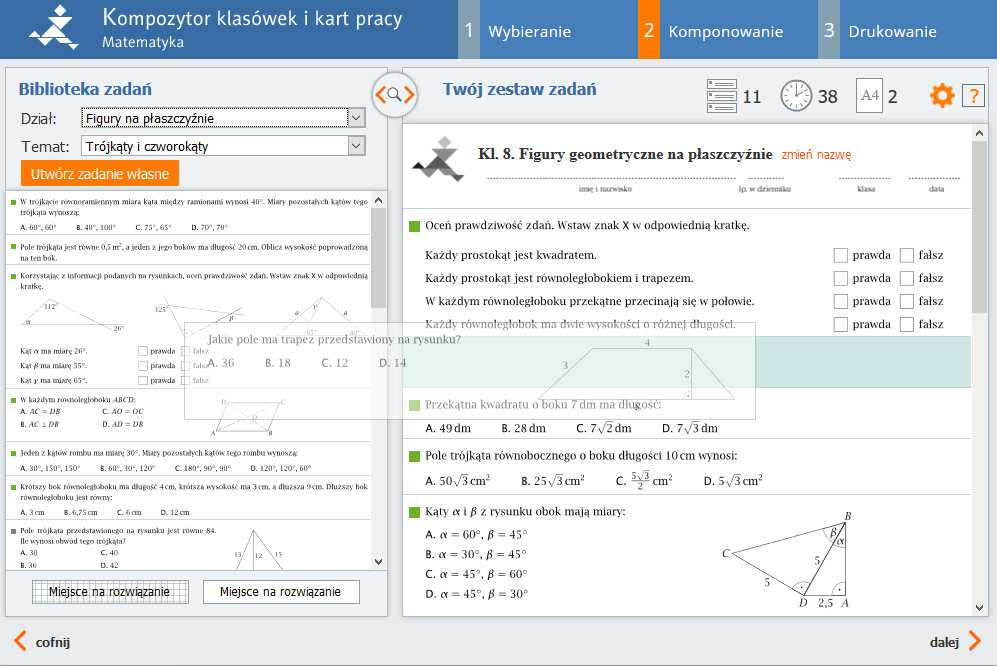
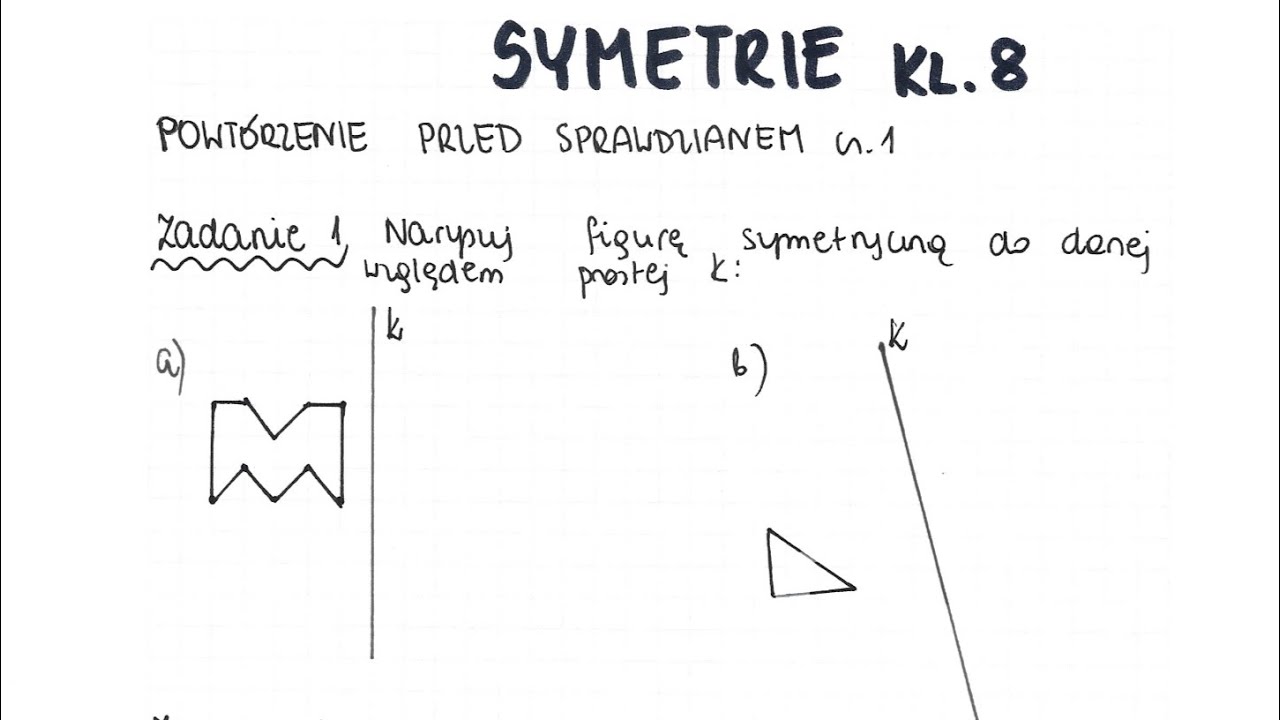
2. Geometria w życiu codziennym

Geometria to nie tylko rysowanie figur. Uczniowie powinni dostrzegać, jak geometria wpływa na architekturę, budownictwo, projektowanie i wiele innych dziedzin. Należy skupić się na:

Obliczaniu powierzchni i objętości różnych obiektów (pokoje, działki, pojemniki).
Wykorzystywaniu twierdzenia Pitagorasa w praktycznych sytuacjach (np. obliczanie długości drabiny opartej o ścianę).
Zastosowaniu podobieństwa figur (np. skalowanie map, projektowanie modeli).

Jak uczyć? Pokażcie uczniom zdjęcia budynków, mostów, konstrukcji inżynierskich i zapytajcie, jakie figury geometryczne w nich widzą. Można też poprosić uczniów o zmierzenie swojego pokoju i obliczenie jego powierzchni i objętości.

3. Równania i nierówności w rozwiązywaniu problemów

Równania i nierówności to potężne narzędzia do rozwiązywania różnorodnych problemów. Uczniowie powinni umieć:

Modelować sytuacje problemowe za pomocą równań i nierówności.
Rozwiązywać równania i nierówności liniowe.
Interpretować rozwiązania w kontekście zadania.

Jak uczyć? Zadawajcie uczniom zadania tekstowe, które wymagają przetłumaczenia na język matematyki. Można wykorzystać zadania związane z ruchem, pracą, mieszaninami itp. Ważne jest, aby uczniowie rozumieli, co oznacza rozwiązanie równania w kontekście zadania.

4. Statystyka i prawdopodobieństwo

Umiejętność analizowania danych statystycznych i obliczania prawdopodobieństwa jest niezbędna w dzisiejszym świecie. Uczniowie powinni:

Umieć odczytywać i interpretować dane z wykresów i tabel.
Obliczać średnią arytmetyczną, medianę i dominantę.
Obliczać prawdopodobieństwo prostych zdarzeń.

Jak uczyć? Wykorzystajcie aktualne dane statystyczne (np. dotyczące demografii, sportu, ekonomii). Można poprosić uczniów o przeprowadzenie ankiety w klasie i przedstawienie wyników na wykresie. Prawdopodobieństwo można wprowadzić za pomocą prostych gier losowych (np. rzut kostką, losowanie kartek).

Typowe Trudności i Jak Sobie z Nimi Radzić

Podczas nauczania Zastosowań Matematyki, uczniowie mogą napotykać na różne trudności. Oto niektóre z nich i sposoby na ich pokonanie:

Trudność w zrozumieniu treści zadania: Naucz uczniów analizować treść zadania krok po kroku, wyodrębniać istotne informacje i identyfikować, co mają obliczyć. Można stosować techniki wizualizacji, takie jak rysowanie schematów lub diagramów.
Trudność w przełożeniu treści zadania na język matematyki: To kluczowy element modelowania matematycznego. Ćwiczcie z uczniami tłumaczenie zdań na równania i nierówności. Można zacząć od prostych przykładów, a następnie stopniowo przechodzić do bardziej złożonych.
Brak umiejętności obliczeniowych: Upewnijcie się, że uczniowie dobrze opanowali podstawowe umiejętności arytmetyczne (dodawanie, odejmowanie, mnożenie, dzielenie, obliczanie procentów). W razie potrzeby, zorganizujcie dodatkowe zajęcia wyrównawcze.
Brak pewności siebie: Zachęcajcie uczniów do zadawania pytań i dzielenia się swoimi wątpliwościami. Stwórzcie atmosferę, w której błędy są traktowane jako okazja do nauki.

Jak Uczynić Lekcje Zastosowań Matematyki Ciekawymi?

Oto kilka pomysłów na to, jak uatrakcyjnić lekcje Zastosowań Matematyki:

Wykorzystujcie gry i zabawy: Matematyka może być zabawą! Wykorzystajcie gry planszowe, karciane, interaktywne quizy online, aby utrwalić wiedzę i umiejętności.
Stosujcie metody aktywizujące: Zamiast wykładu, poproście uczniów o pracę w grupach, rozwiązywanie problemów, prezentowanie wyników.
Wykorzystujcie technologię: Skorzystajcie z kalkulatorów, programów komputerowych, aplikacji mobilnych, aby wizualizować zagadnienia matematyczne i ułatwić obliczenia.
Pokazujcie praktyczne zastosowania: Przynoście na lekcje przedmioty, z którymi uczniowie stykają się na co dzień (np. opakowania, mapy, reklamy) i analizujcie je pod kątem matematycznym.
Organizujcie projekty edukacyjne: Poproście uczniów o przeprowadzenie badań statystycznych, zaprojektowanie budżetu domowego, zaplanowanie podróży, obliczenie kosztów remontu itp.

Pamiętajcie, że kluczem do sukcesu jest cierpliwość, empatia i indywidualne podejście do każdego ucznia. Powodzenia!