Zasada Zachowania Energii Zadania

Cześć! Pewnie tak jak wielu innych, zmagasz się z zadaniami z zasady zachowania energii. Nie martw się, to częsty problem! Fizyka potrafi być skomplikowana, a energia, choć wszechobecna, czasami wydaje się trudna do uchwycenia. Mam nadzieję, że ten artykuł pomoże Ci lepiej zrozumieć tę fundamentalną zasadę i ułatwi rozwiązywanie zadań.

Wiem, jak frustrujące może być wpatrywanie się w zadanie, w którym coś spada, zjeżdża, albo się toczy, i nie wiedzieć, od czego zacząć. Często czujemy się zagubieni w gąszczu wzorów i definicji, zapominając o tym, co najważniejsze: energia nigdzie nie ginie, tylko się przekształca.

Co to właściwie jest zasada zachowania energii?

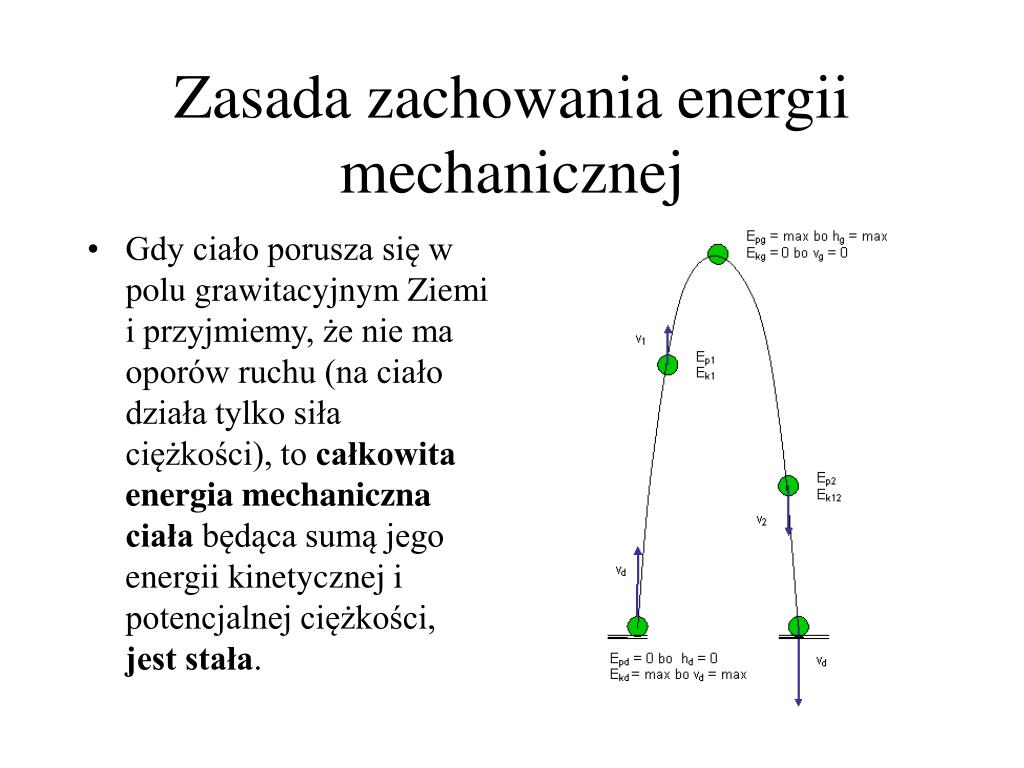
Zasada zachowania energii to jeden z fundamentów fizyki. Mówi ona, że w izolowanym układzie całkowita ilość energii pozostaje stała. Inaczej mówiąc, energia nie może być stworzona ani zniszczona, a jedynie przekształcana z jednej formy w inną.

Wyobraź sobie zamknięty system: termos z gorącą kawą. Energia cieplna kawy nie zniknie (przynajmniej idealnie), tylko stopniowo przekształci się w energię cieplną otoczenia. Im lepiej izolowany termos, tym wolniej ten proces zachodzi.

Różne formy energii

Aby zrozumieć zasadę zachowania energii, musimy znać różne formy energii:

• Energia kinetyczna (E_k): Energia związana z ruchem. Im większa masa i prędkość ciała, tym większa jego energia kinetyczna. Wzór: E_k = (1/2)mv²
• Energia potencjalna (E_p): Energia związana z położeniem ciała w polu sił. Wyróżniamy:
  • Energia potencjalna grawitacji: Związana z wysokością ciała nad powierzchnią ziemi. Wzór: E_p = mgh (gdzie g to przyspieszenie ziemskie).
  • Energia potencjalna sprężystości: Związana z odkształceniem sprężystym ciała, np. sprężyny. Wzór: E_p = (1/2)kx² (gdzie k to współczynnik sprężystości, a x to odkształcenie).
• Energia cieplna: Energia związana z ruchem cząsteczek w ciele.
• Energia elektryczna: Energia związana z przepływem ładunków elektrycznych.
• Energia chemiczna: Energia zmagazynowana w wiązaniach chemicznych.
• Energia jądrowa: Energia zmagazynowana w jądrach atomów.

Jak rozwiązywać zadania z zasadą zachowania energii?

Oto kilka kroków, które pomogą Ci uporać się z zadaniami:

1. Zrozum zadanie: Przeczytaj uważnie zadanie i upewnij się, że rozumiesz, co się dzieje. Określ, co jest dane, a co trzeba znaleźć.
2. Zidentyfikuj układ: Określ, co wchodzi w skład Twojego układu. Czy jest to tylko spadające ciało, czy może ciało i sprężyna? Czy układ jest izolowany? (Czyli czy nie działają na niego siły zewnętrzne, które mogłyby zmieniać jego energię).
3. Wybierz dwa punkty: Wybierz dwa charakterystyczne punkty w układzie, np. początkowy i końcowy.
4. Określ formy energii: W każdym z wybranych punktów określ, jakie formy energii występują. Czy ciało ma energię kinetyczną, potencjalną grawitacji, potencjalną sprężystości?
5. Zapisz równanie zachowania energii: Suma energii w punkcie początkowym równa się sumie energii w punkcie końcowym.
   E_początkowa = E_końcowa
   Np.: E_k1 + E_p1 = E_k2 + E_p2
6. Rozwiąż równanie: Podstaw wartości liczbowe i rozwiąż równanie, aby znaleźć szukaną wielkość.

Przykłady zadań

Przykład 1: Spadające jabłko

Jabłko o masie 0.2 kg spada z drzewa z wysokości 3 m. Oblicz jego prędkość tuż przed uderzeniem o ziemię (pomijamy opór powietrza).

1. Zrozumienie: Jabłko spada, zamieniając energię potencjalną w kinetyczną.
2. Układ: Jabłko. Układ jest izolowany (pomijamy opór powietrza).
3. Punkty: Punkt początkowy (na wysokości 3 m) i punkt końcowy (tuż nad ziemią).
4. Formy energii:
   • Punkt początkowy: E_p = mgh, E_k = 0 (jabłko spoczywa)
   • Punkt końcowy: E_p = 0 (wysokość = 0), E_k = (1/2)mv²
5. Równanie: mgh = (1/2)mv²
6. Rozwiązanie: v = √(2gh) = √(2 * 9.81 m/s² * 3 m) ≈ 7.67 m/s

Przykład 2: Sprężyna i kulka

Kulka o masie 0.1 kg spada na pionowo ustawioną sprężynę o współczynniku sprężystości k = 100 N/m z wysokości 0.5 m (licząc od wierzchołka sprężyny). Oblicz maksymalne ściśnięcie sprężyny.

1. Zrozumienie: Kulka traci energię potencjalną grawitacji, która przekształca się w energię potencjalną sprężystości.
2. Układ: Kulka i sprężyna. Układ jest izolowany (pomijamy opory).
3. Punkty: Punkt początkowy (na wysokości 0.5 m nad sprężyną) i punkt końcowy (maksymalne ściśnięcie sprężyny).
4. Formy energii:
   • Punkt początkowy: E_{p grawitacji} = mg(h+x), E_k = 0, E_{p sprężystości} = 0
   • Punkt końcowy: E_{p grawitacji} = 0 (bierzemy punkt odniesienia na wysokości maksymalnego ściśnięcia), E_k = 0 (kulka się zatrzymuje), E_{p sprężystości} = (1/2)kx²
5. Równanie: mg(h+x) = (1/2)kx²
6. Rozwiązanie: To równanie kwadratowe. Po podstawieniu wartości: 0.1 * 9.81 * (0.5 + x) = (1/2) * 100 * x².
   Upraszczając: 4.905 + 0.981x = 50x²
   Przekształcając: 50x² - 0.981x - 4.905 = 0
   Rozwiązując równanie kwadratowe (np. za pomocą kalkulatora): x ≈ 0.323 m

Pułapki i błędy

Podczas rozwiązywania zadań z zasadą zachowania energii, często popełniamy błędy. Oto kilka najczęstszych:

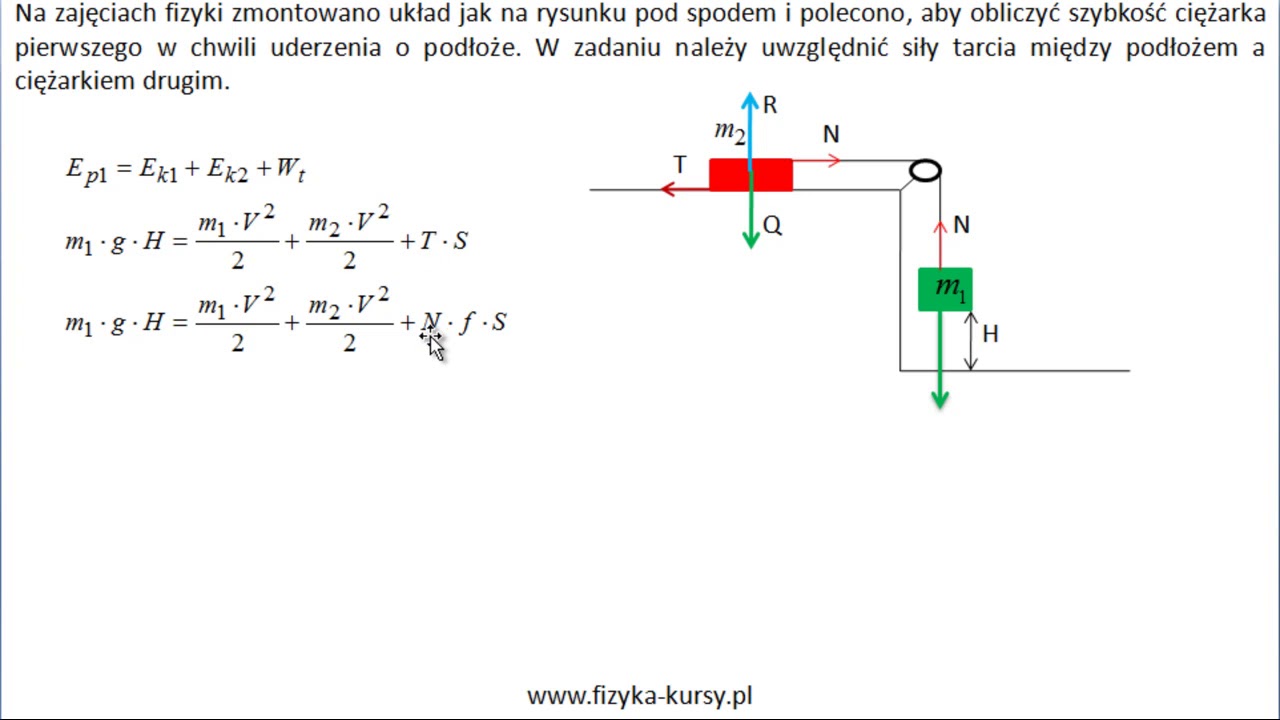
• Pomijanie sił tarcia i oporu powietrza: W rzeczywistości siły tarcia i oporu powietrza zawsze występują i powodują straty energii. Często w zadaniach są one pomijane, ale trzeba o tym pamiętać. Jeśli w zadaniu jest powiedziane, że należy uwzględnić tarcie, należy obliczyć pracę siły tarcia i dodać ją do równania zachowania energii (jako stratę energii).
• Źle zdefiniowany układ: Zdefiniowanie odpowiedniego układu jest kluczowe. Jeśli układ nie jest izolowany, zasada zachowania energii nie działa bezpośrednio.
• Błędne obliczenia energii potencjalnej: Należy pamiętać, że energia potencjalna zależy od wybranego poziomu odniesienia. Ważne jest, aby konsekwentnie stosować ten sam poziom odniesienia w całym zadaniu.
• Zapominanie o energii kinetycznej obrotowej: Jeśli ciało się toczy, ma również energię kinetyczną obrotową.

Kontrowersje i alternatywne punkty widzenia?

Czy zasada zachowania energii jest zawsze prawdziwa? W zasadzie tak, ale istnieją pewne subtelności. W ogólnej teorii względności, w kontekście rozszerzającego się wszechświata, definicja energii staje się bardziej skomplikowana i trudniej jest jednoznacznie zdefiniować całkowitą energię. Jednak na poziomie, na którym rozwiązujemy większość zadań z fizyki, zasada zachowania energii jest doskonałym narzędziem i wspaniałym przybliżeniem.

Czasami słyszymy o pomysłach na "darmową energię" (perpetuum mobile). Zasada zachowania energii jasno pokazuje, że takie urządzenie jest niemożliwe. Musiałoby ono naruszać podstawowe prawa fizyki.

Jak zastosować zasadę zachowania energii w życiu codziennym?

Zasada zachowania energii ma ogromne znaczenie w inżynierii, technologii i naszym codziennym życiu. Oto kilka przykładów:

• Projektowanie efektywnych energetycznie budynków: Wykorzystując izolację, możemy ograniczyć straty ciepła i zaoszczędzić energię.
• Rozwój odnawialnych źródeł energii: Energia słoneczna, wiatrowa i wodna to przykłady wykorzystania naturalnych procesów przekształcania energii.
• Optymalizacja transportu: Projektowanie samochodów o niskim oporze powietrza i hybrydowych układów napędowych pozwala zmniejszyć zużycie paliwa.

Zrozumienie zasady zachowania energii pozwala nam świadomie korzystać z zasobów i podejmować decyzje, które są bardziej przyjazne dla środowiska.

Pamiętaj, że kluczem do sukcesu w rozwiązywaniu zadań z fizyki jest ćwiczenie i dogłębne zrozumienie podstawowych zasad. Nie zniechęcaj się, jeśli początki są trudne. Każdy fizyk kiedyś zaczynał od zera.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć zasadę zachowania energii. Czy masz jakieś pytania lub uwagi? Zachęcam Cię do dalszego zgłębiania tego fascynującego tematu!