Zasada Zachowania Energii Mechanicznej

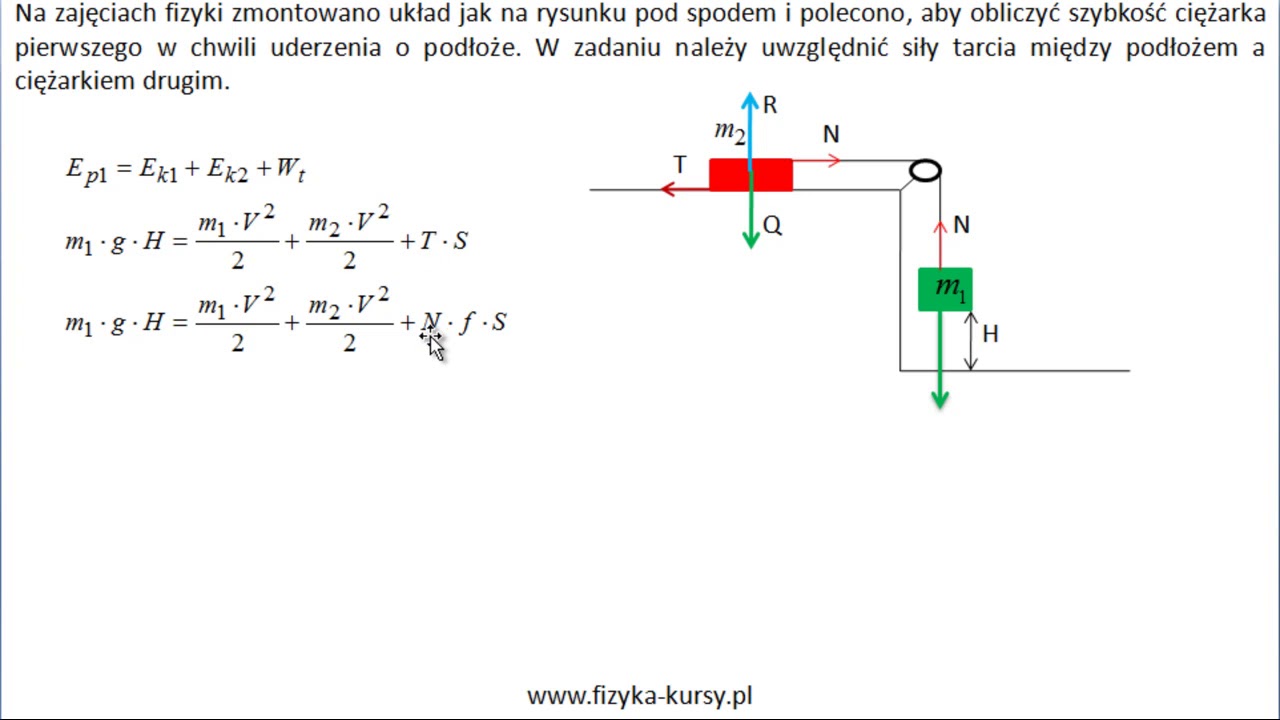
Czy kiedykolwiek zastanawiałeś się, dlaczego huśtawka w końcu się zatrzymuje? Albo jak piłka odbija się, ale nigdy nie wraca na tę samą wysokość, z której została upuszczona? Odpowiedź tkwi w fundamentalnej zasadzie fizyki: Zasadzie Zachowania Energii Mechanicznej. Ten artykuł został stworzony dla uczniów, studentów i wszystkich ciekawych świata, którzy chcą zrozumieć podstawy tej ważnej koncepcji.

Choć w życiu codziennym obserwujemy procesy, które zdają się zaprzeczać tej zasadzie, to w idealnych warunkach jest ona niezachwiana. Przyjrzyjmy się zatem, co kryje się za tym stwierdzeniem i jak znajduje ono zastosowanie w praktyce.

Co to jest Energia Mechaniczna?

Zanim przejdziemy do samej zasady, musimy zrozumieć, czym właściwie jest energia mechaniczna. Możemy ją podzielić na dwa główne rodzaje:

• Energia Kinetyczna (Ek): Energia związana z ruchem. Im szybciej porusza się obiekt, tym większa jest jego energia kinetyczna. Zależy ona od masy obiektu (m) i jego prędkości (v): Ek = 1/2 * m * v².
• Energia Potencjalna (Ep): Energia związana z położeniem lub konfiguracją obiektu. W najprostszym przypadku rozważamy:
  • Energia Potencjalna Grawitacji: Energia, którą obiekt posiada ze względu na swoje położenie w polu grawitacyjnym. Zależy od masy obiektu (m), przyspieszenia ziemskiego (g) i wysokości (h): Ep = m * g * h.
  • Energia Potencjalna Sprężystości: Energia zmagazynowana w odkształconym ciele sprężystym, np. naciągniętej sprężynie.

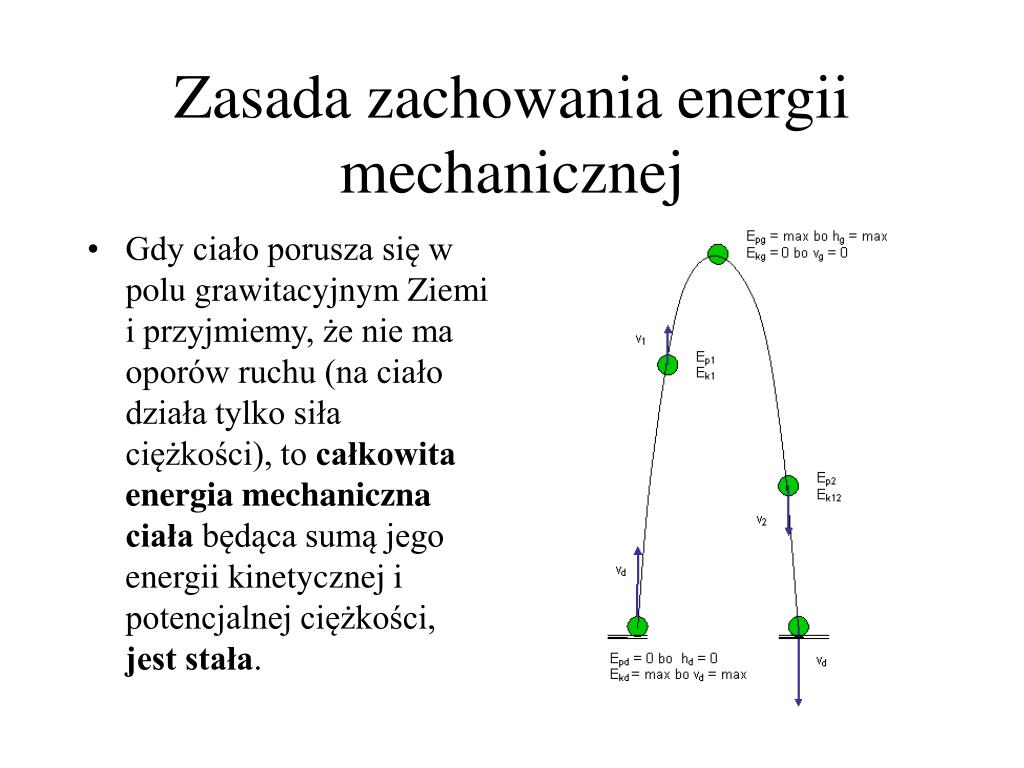
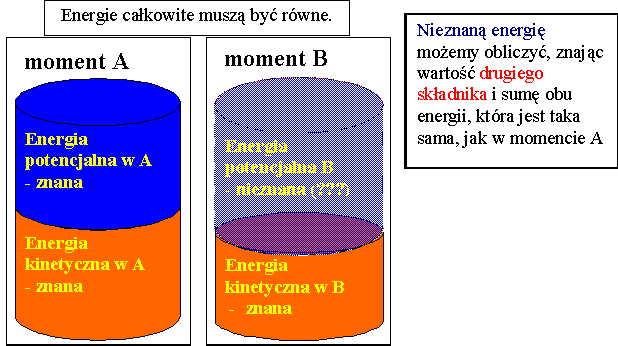
Suma energii kinetycznej i potencjalnej nazywana jest całkowitą energią mechaniczną (E): E = Ek + Ep.

Zasada Zachowania Energii Mechanicznej – Istota

Zasada Zachowania Energii Mechanicznej mówi, że w układzie izolowanym (czyli takim, na który nie działają siły zewnętrzne inne niż siły zachowawcze), całkowita energia mechaniczna pozostaje stała. Oznacza to, że energia może przekształcać się z jednej formy w drugą (np. energia potencjalna w kinetyczną i odwrotnie), ale jej suma pozostaje niezmienna.

W układzie izolowanym, gdzie działają jedynie siły zachowawcze, całkowita energia mechaniczna jest stała: E = Ek + Ep = const

Siły zachowawcze to takie siły, dla których praca wykonana przez siłę zależy tylko od punktu początkowego i końcowego, a nie od drogi. Przykładami są siła grawitacji i siła sprężystości. Siły niezachowawcze (np. tarcie) powodują rozpraszanie energii mechanicznej w postaci ciepła, dźwięku, itp.

Idealny Świat – Brak Tarcia i Opór Powietrza

Zanim przejdziemy dalej, musimy zaznaczyć, że Zasada Zachowania Energii Mechanicznej obowiązuje ściśle tylko w idealnych warunkach, czyli tam, gdzie nie występują siły niezachowawcze, takie jak tarcie i opór powietrza. W realnym świecie te siły zawsze są obecne i powodują, że część energii mechanicznej jest tracona (zamieniana na inne formy energii, np. ciepło).

Jednak w wielu sytuacjach możemy je zaniedbać, aby uprościć analizę problemu.

Przykłady Zastosowania Zasady

Aby lepiej zrozumieć Zasadę Zachowania Energii Mechanicznej, przyjrzyjmy się kilku przykładom:

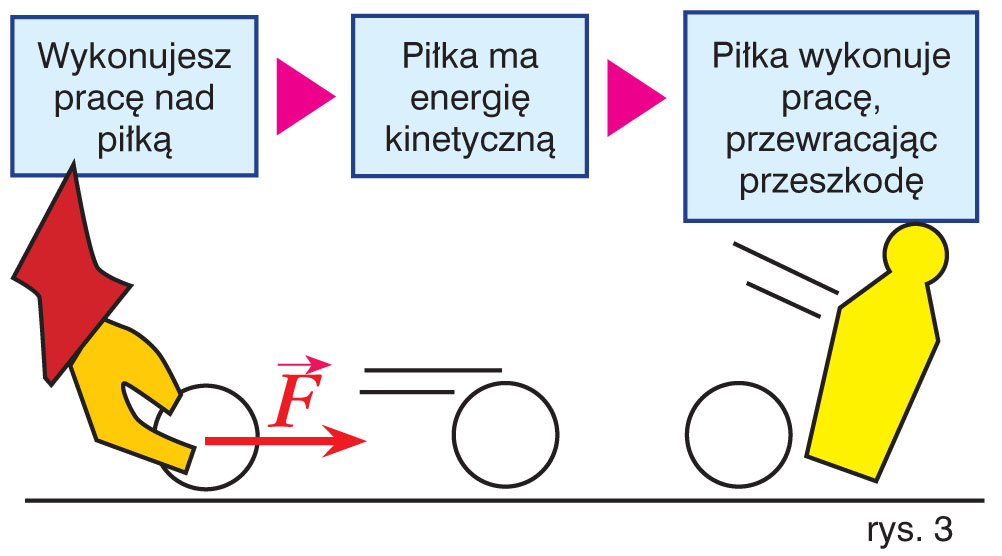
• Spadanie swobodne: Gdy upuszczamy piłkę z pewnej wysokości, jej energia potencjalna grawitacji zamienia się w energię kinetyczną. Na samej górze piłka ma maksymalną energię potencjalną i zerową energię kinetyczną. Tuż przed uderzeniem o ziemię, energia potencjalna jest minimalna (w zasadzie zerowa), a energia kinetyczna – maksymalna. W idealnym przypadku, suma tych dwóch energii w każdym punkcie trajektorii jest taka sama.
• Huśtawka: Gdy huśtamy się, w najwyższym punkcie ruchu mamy maksymalną energię potencjalną i zerową energię kinetyczną. W najniższym punkcie – odwrotnie. Energia ciągle przekształca się z potencjalnej w kinetyczną i z powrotem. Niestety, tarcie i opór powietrza powodują, że energia mechaniczna jest stopniowo tracona, i huśtawka w końcu się zatrzymuje.
• Wahadło: Podobnie jak na huśtawce, wahadło ciągle przekształca energię potencjalną w kinetyczną i z powrotem. W najwyższych punktach trajektorii wahadło ma maksymalną energię potencjalną i zerową energię kinetyczną, a w najniższym – odwrotnie. Bez tarcia, wahadło huśtałoby się bez końca!
• Jazda na rollercoasterze: Podczas jazdy na rollercoasterze energia potencjalna zamienia się w kinetyczną podczas zjazdu z górki, a kinetyczna w potencjalną podczas wjazdu na następną. Projektanci rollercoasterów muszą brać pod uwagę tę zasadę, aby zapewnić odpowiednią prędkość wagoników w każdym punkcie trasy.

Jak rozwiązywać zadania z wykorzystaniem zasady zachowania energii?

Rozwiązywanie zadań z wykorzystaniem Zasady Zachowania Energii Mechanicznej zazwyczaj przebiega według następującego schematu:

1. Zdefiniuj układ: Określ, jakie obiekty wchodzą w skład układu i jakie siły na nie działają.
2. Zidentyfikuj siły zachowawcze i niezachowawcze: Ustal, czy działają siły niezachowawcze (np. tarcie). Jeśli ich wpływ jest pomijalny, możemy zastosować zasadę zachowania energii mechanicznej.
3. Wybierz dwa charakterystyczne punkty: Wybierz dwa punkty w ruchu, w których łatwo obliczyć energię kinetyczną i potencjalną. Na przykład, punkt początkowy i końcowy ruchu.
4. Zapisz równanie zachowania energii: Zapisz równanie, które mówi, że całkowita energia mechaniczna w punkcie początkowym jest równa całkowitej energii mechanicznej w punkcie końcowym: Ek1 + Ep1 = Ek2 + Ep2.
5. Oblicz energie: Oblicz energię kinetyczną i potencjalną w obu punktach.
6. Rozwiąż równanie: Rozwiąż równanie, aby znaleźć szukaną wielkość.

Przykład:

Ciało o masie m = 2 kg spada swobodnie z wysokości h = 5 m. Oblicz jego prędkość tuż przed uderzeniem o ziemię, pomijając opór powietrza.

Rozwiązanie:

1. Punkt początkowy: ciało na wysokości h. Punkt końcowy: ciało tuż przed uderzeniem o ziemię.
2. Ek1 + Ep1 = Ek2 + Ep2
3. 0 + mgh = 1/2mv² + 0 (W punkcie początkowym prędkość jest zerowa, a w punkcie końcowym wysokość jest zerowa)
4. mgh = 1/2mv²
5. gh = 1/2v²
6. v = √(2gh) = √(2 * 9.81 m/s² * 5 m) ≈ 9.9 m/s

Zatem prędkość ciała tuż przed uderzeniem o ziemię wynosi około 9.9 m/s.

Dlaczego ta wiedza jest ważna?

Zrozumienie Zasady Zachowania Energii Mechanicznej jest kluczowe nie tylko w fizyce, ale również w wielu innych dziedzinach nauki i techniki. Pozwala nam projektować bardziej efektywne maszyny, optymalizować procesy i lepiej rozumieć otaczający nas świat.

Wyobraź sobie inżyniera projektującego elektrownię wodną. Musi on dokładnie obliczyć energię potencjalną wody zgromadzonej w zbiorniku i jej transformację w energię kinetyczną, która napędza turbiny. Bez zrozumienia zasady zachowania energii, projektowanie takiej elektrowni byłoby niemożliwe.

Zasada Zachowania Energii Mechanicznej jest fundamentem zrozumienia wielu zjawisk fizycznych i technologicznych. Daje nam narzędzia do analizy i przewidywania zachowania układów mechanicznych, co jest niezwykle cenne w wielu dziedzinach życia.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć tę fundamentalną zasadę. Pamiętaj, że fizyka to nie tylko wzory, ale przede wszystkim sposób patrzenia na świat! Zachęcam do dalszego zgłębiania tej fascynującej dziedziny wiedzy.