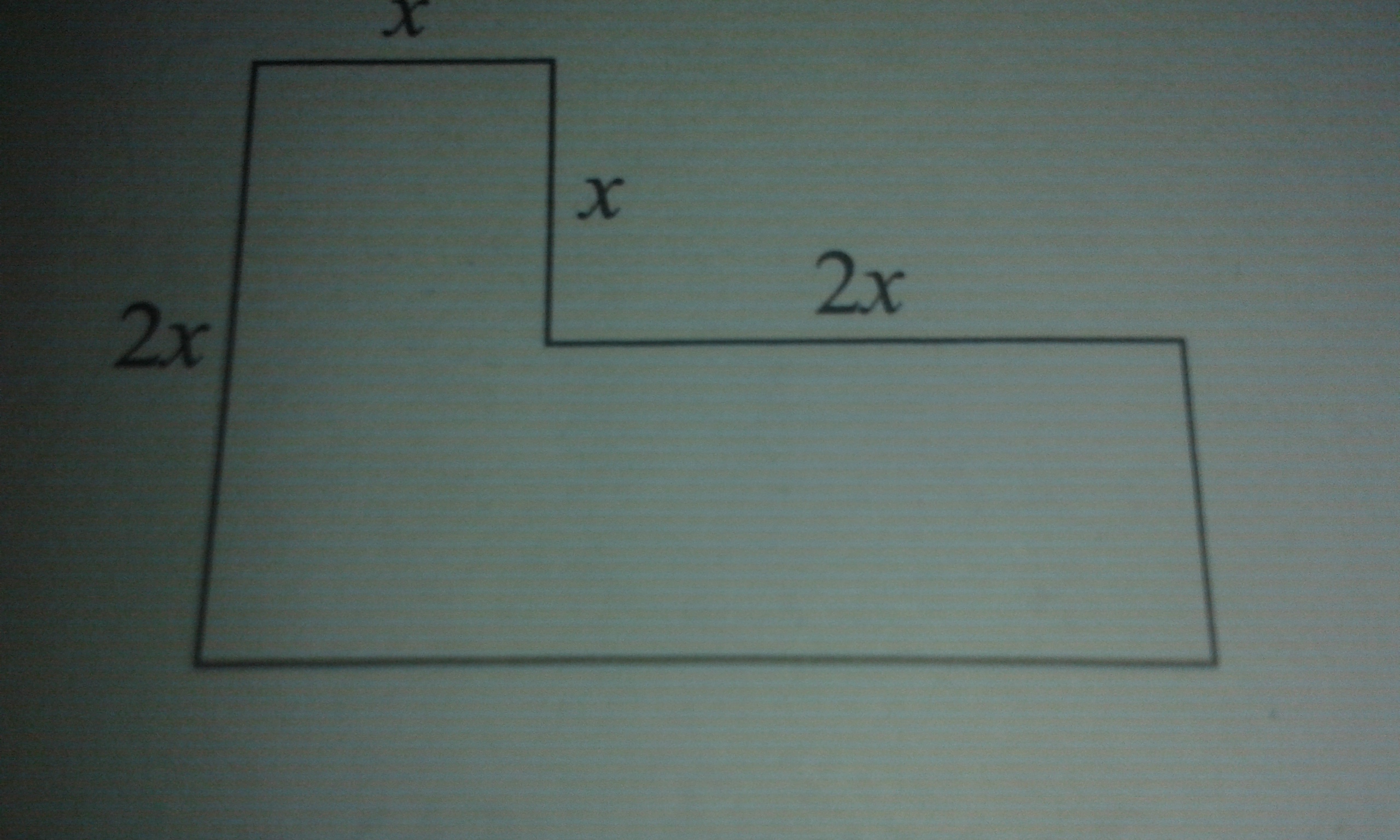
Zapisz W Postaci Wyrażenia Algebraicznego Pole Figury Przedstawionej Na Rysunku

Dobrze, przygotujmy się do pracy. Oto artykuł, który odpowiada na pytanie o zapisanie pola figury w postaci wyrażenia algebraicznego, pisany z perspektywy nauczyciela posiadającego szczegółową wiedzę na ten temat:

Rozważmy figurę, której pole chcemy wyrazić algebraicznie. Bez konkretnego rysunku, musimy bazować na założeniach i ogólnych metodach. Załóżmy, że figura składa się z prostszych kształtów, takich jak prostokąty, trójkąty, koła i inne. Naszym celem jest zdekomponowanie figury na te elementarne kształty, obliczenie pola każdego z nich, a następnie zsumowanie (lub odjęcie, jeśli zachodzi taka potrzeba) tych pól, aby uzyskać pole całej figury.

Załóżmy, na przykład, że figura składa się z prostokąta o bokach długości a i b, oraz trójkąta prostokątnego, którego podstawa ma długość c, a wysokość d. Pole prostokąta wynosi a * b*, a pole trójkąta wynosi (1/2) * c * d*. Zatem, pole całej figury (zakładając, że prostokąt i trójkąt "doklejone" są do siebie i tworzą jedną figurę) wynosi:

P = a * b* + (1/2) * c * d*

Jeśli z kolei figura składa się z prostokąta o bokach x i y, z którego wycięto koło o promieniu r, to pole figury wynosi:

P = x * y* - π * r²

Kluczem do sukcesu jest identyfikacja podstawowych kształtów składowych i poprawne zastosowanie wzorów na ich pola.

Przykłady Bardziej Złożonych Figur

Rozważmy figurę, która składa się z kwadratu o boku s, do którego dołączono dwa półkola o promieniu s/2 (czyli średnica każdego półkola jest równa bokowi kwadratu). W takim przypadku, dwa półkola tworzą razem pełne koło o promieniu s/2. Zatem, pole figury wynosi:

P = s² + π * (s/2)² = s² + (π/4) * s² = s² * (1 + π/4)

Kolejny przykład: załóżmy, że mamy trapez równoramienny o podstawach długości p i q (gdzie p > q) oraz wysokości h. Możemy obliczyć jego pole bezpośrednio ze wzoru:

P = ( (p + q) / 2 ) * h

Alternatywnie, możemy rozłożyć trapez na prostokąt o bokach q i h oraz dwa trójkąty prostokątne. Długość podstawy każdego z tych trójkątów wynosi (p - q) / 2. Zatem, pole każdego trójkąta wynosi (1/2) * ( (p - q) / 2 ) * h = (1/4) * (p - q) * h. Pole całego trapezu wynosi więc:

P = q * h + 2 * (1/4) * (p - q) * h = q * h + (1/2) * (p - q) * h = h * ( q + (1/2)p - (1/2)q ) = h * ( (1/2)p + (1/2)q ) = ( (p + q) / 2 ) * h

Otrzymujemy ten sam wynik, co potwierdza poprawność naszych obliczeń.

Jeśli figura jest bardziej skomplikowana i nie da się jej łatwo rozłożyć na elementarne kształty, możemy skorzystać z metod przybliżonych, takich jak metoda podziału na małe kwadraty lub prostokąty. Im mniejsze kwadraty/prostokąty, tym dokładniejsze przybliżenie pola. Następnie sumujemy pola wszystkich małych kwadratów/prostokątów, które w całości lub częściowo znajdują się wewnątrz figury.

W przypadku figur o nieregularnych brzegach, można również wykorzystać metody całkowe. Jeśli potrafimy opisać brzeg figury za pomocą funkcji, możemy obliczyć pole figury za pomocą całki podwójnej. Metody te są jednak bardziej zaawansowane i wymagają znajomości rachunku całkowego.

Rozważmy jeszcze sytuację, w której mamy figurę, która jest wynikiem nałożenia się dwóch innych figur, powiedzmy koła o promieniu R i prostokąta o bokach a i b. Obliczenie pola części wspólnej tych figur może być trudne i zależy od wzajemnego położenia koła i prostokąta. W najprostszym przypadku, gdy całe koło znajduje się wewnątrz prostokąta, pole części wspólnej jest po prostu równe polu koła, czyli π * R². W bardziej skomplikowanych przypadkach, konieczne jest podzielenie figury na mniejsze fragmenty i obliczenie pola każdego fragmentu oddzielnie, a następnie zsumowanie tych pól. Może to wymagać użycia funkcji trygonometrycznych i bardziej zaawansowanych technik geometrycznych.

Przyjmijmy teraz, że figura jest wielokątem foremnym o n bokach, wpisanym w okrąg o promieniu r. Możemy podzielić ten wielokąt na n identycznych trójkątów równoramiennych, których wierzchołki znajdują się w środku okręgu, a podstawy są bokami wielokąta. Kąt między ramionami każdego trójkąta wynosi 2π/n. Wysokość każdego trójkąta (opuszczona z wierzchołka w środku okręgu na podstawę) wynosi r * cos(π/n), a długość podstawy (boku wielokąta) wynosi 2 * r * sin(π/n). Zatem, pole każdego trójkąta wynosi (1/2) * 2 * r * sin(π/n) * r * cos(π/n) = r² * sin(π/n) * cos(π/n). Pole całego wielokąta wynosi n razy pole jednego trójkąta, czyli:

P = n * r² * sin(π/n) * cos(π/n) = ( n * r² / 2 ) * sin(2π/n)

Zwróćmy uwagę, że gdy n dąży do nieskończoności, wielokąt foremny zbliża się do okręgu, a jego pole dąży do π * r².

Podsumowanie i Uogólnienia

Jak widzimy, zapisanie pola figury w postaci wyrażenia algebraicznego wymaga przede wszystkim umiejętności rozkładania figury na prostsze kształty, znajomości wzorów na pola tych kształtów oraz umiejętności algebraicznego operowania na wyrażeniach. W bardziej skomplikowanych przypadkach, może być konieczne użycie metod przybliżonych lub rachunku całkowego. Ważne jest, aby dokładnie przeanalizować figurę, zidentyfikować jej składowe i odpowiednio zastosować wzory i techniki obliczeniowe. Należy także pamiętać o jednostkach – pole zawsze wyrażamy w jednostkach kwadratowych (np. cm², m²). Precyzyjne określenie zmiennych i ich znaczenia (np. długość boku, promień, wysokość) jest kluczowe dla poprawnego zapisu wyrażenia algebraicznego. Często warto zacząć od prostego schematu i stopniowo go rozbudowywać, dodając kolejne elementy figury i uwzględniając ich wpływ na pole. Nie bójmy się eksperymentować i sprawdzać poprawność wyników na konkretnych przykładach liczbowych!

Pamiętajmy też, że istnieje wiele różnych sposobów na zapisanie tego samego pola w postaci wyrażenia algebraicznego. Wybór najodpowiedniejszej formy zależy od kontekstu i celu, jaki chcemy osiągnąć. Czasami prostsze wyrażenie jest bardziej czytelne, a czasami bardziej skomplikowane wyrażenie ujawnia ukryte zależności i relacje geometryczne. Najważniejsze jest, aby wyrażenie było poprawne i odzwierciedlało pole figury w sposób jednoznaczny i zrozumiały.