Zaokrąglanie Liczb Klasa 6 Zadania

Czy kiedykolwiek zastanawiałeś się, jak ułatwić sobie życie, gdy operujesz dużymi liczbami? A może masz wrażenie, że wynik obliczeń jest zbyt dokładny i niepotrzebnie skomplikowany? W klasie 6 zaczynamy przygodę z zaokrąglaniem liczb, które jest niezwykle przydatną umiejętnością zarówno w matematyce, jak i w codziennym życiu. Zrozumienie zasad zaokrąglania otwiera nowe możliwości upraszczania obliczeń i prezentowania danych w bardziej przejrzysty sposób. Ten artykuł pomoże Ci zrozumieć, na czym polega zaokrąglanie, jakie są jego reguły i jak stosować je w praktycznych zadaniach.

Dlaczego Zaokrąglamy Liczby?

Zaokrąglanie to proces upraszczania liczby poprzez zmniejszenie liczby jej cyfr, zachowując przy tym jej przybliżoną wartość. Robimy to z kilku powodów:

Uproszczenie obliczeń: Praca z mniejszą liczbą cyfr jest łatwiejsza i szybsza.
Przejrzystość: Duże liczby z wieloma miejscami po przecinku mogą być trudne do odczytania i zrozumienia. Zaokrąglona liczba często jest bardziej czytelna i zrozumiała.
Dostosowanie do potrzeb: W niektórych sytuacjach dokładność do kilku miejsc po przecinku jest zbędna. Na przykład, jeśli mówimy o liczbie osób w mieście, zaokrąglenie do tysięcy jest wystarczające.
Ograniczenia pomiarowe: Często nasze narzędzia pomiarowe mają ograniczoną dokładność. Nie ma sensu podawać wyniku z większą dokładnością niż ta, którą możemy realnie zmierzyć.

Wyobraź sobie, że mierzysz długość pokoju i otrzymujesz wynik 3,478 metrów. Czy naprawdę potrzebujesz tej dokładności do milimetra? Prawdopodobnie nie. Zaokrąglenie do 3,5 metra jest w zupełności wystarczające i o wiele łatwiejsze do zapamiętania.

Podstawowe Zasady Zaokrąglania

Zaokrąglanie liczb odbywa się zgodnie z pewnymi zasadami. Najważniejsze z nich to:

1. Określenie Miejsca Zaokrąglenia

Musimy najpierw zdecydować, do jakiej cyfry chcemy zaokrąglić. Może to być do jedności, dziesiątek, setek, części dziesiątych, części setnych itd. Mówiąc prościej, musimy ustalić, do którego miejsca chcemy "odciąć" liczbę.

Na przykład, jeśli chcemy zaokrąglić liczbę 123,45 do jedności, to "odcinamy" liczbę po cyfrze 3.

2. Obserwacja Cyfry Następnej

Patrzymy na cyfrę bezpośrednio po cyfrze, do której zaokrąglamy. To ona decyduje o tym, czy zaokrąglamy w górę, czy w dół.

W naszym przykładzie, zaokrąglając 123,45 do jedności, patrzymy na cyfrę 4.

3. Reguła "5 i więcej – w górę, mniej niż 5 – w dół"

Jeśli cyfra, którą obserwujemy, jest 5 lub większa (5, 6, 7, 8, 9), to cyfrę, do której zaokrąglamy, zwiększamy o 1. Jeśli cyfra jest mniejsza niż 5 (0, 1, 2, 3, 4), to cyfrę, do której zaokrąglamy, pozostawiamy bez zmian, a wszystkie cyfry po niej "odcinamy".

W naszym przykładzie, 4 jest mniejsze niż 5, więc zaokrąglamy w dół. 123,45 zaokrąglone do jedności to 123.

4. Zaokrąglanie w Górę i w Dół

Zaokrąglanie w górę oznacza zwiększenie cyfry, do której zaokrąglamy, o 1. Zaokrąglanie w dół oznacza pozostawienie tej cyfry bez zmian.

Przykłady Zaokrąglania

Spójrzmy na kilka przykładów, aby lepiej zrozumieć zasady zaokrąglania:

Zaokrąglenie do jedności:
- 3,14 ≈ 3 (bo 1 < 5)
- 7,89 ≈ 8 (bo 8 > 5)
- 12,5 ≈ 13 (bo 5 = 5)
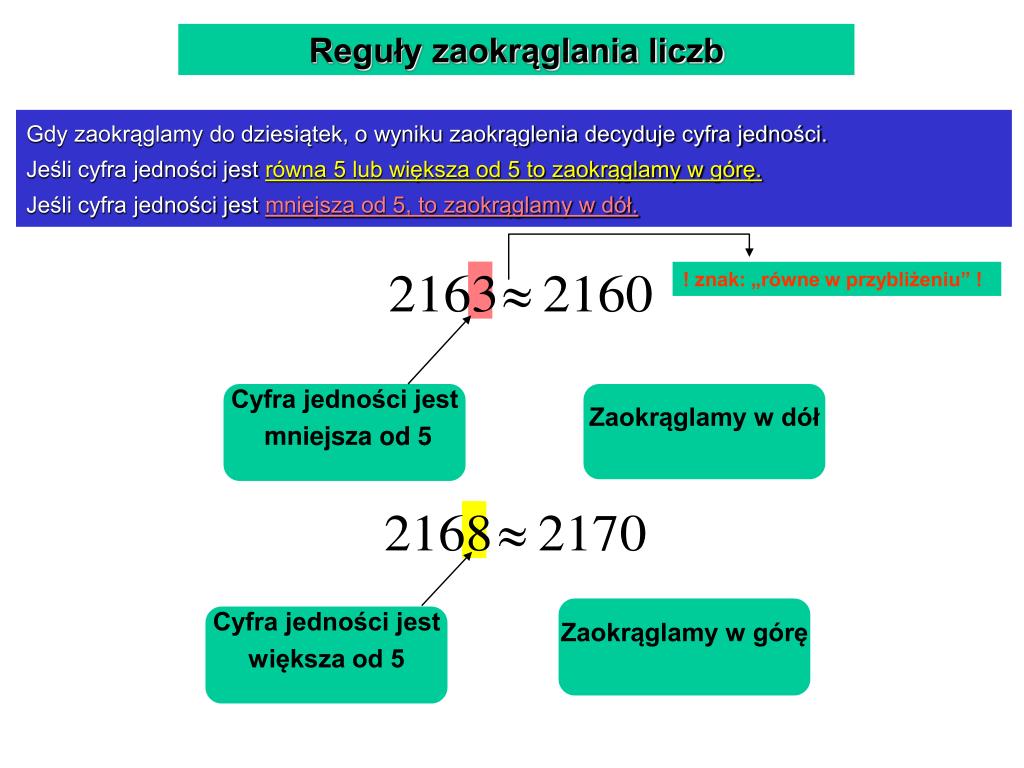
Zaokrąglenie do dziesiątek:
- 45 ≈ 50 (bo 5 = 5)
- 72 ≈ 70 (bo 2 < 5)
- 189 ≈ 190 (bo 9 > 5)
Zaokrąglenie do setnych:
- 1,234 ≈ 1,23 (bo 4 < 5)
- 5,678 ≈ 5,68 (bo 8 > 5)
- 0,995 ≈ 1,00 (bo 5 = 5, a zaokrąglając 9 w górę otrzymujemy 10, więc przenosimy 1 do poprzedniej cyfry)

Zadania Praktyczne z Zaokrąglaniem

Teraz przejdźmy do kilku zadań, aby sprawdzić, jak dobrze opanowałeś zasady zaokrąglania. Spróbuj rozwiązać je samodzielnie, a następnie sprawdź swoje odpowiedzi.

Zaokrąglij liczbę 15,73 do jedności.
Zaokrąglij liczbę 246,8 do dziesiątek.
Zaokrąglij liczbę 3,14159 do części setnych.
Zaokrąglij liczbę 999,99 do jedności.
Zaokrąglij liczbę 0,007 do części setnych.

Rozwiązania:

16 (bo 7 > 5)
250 (bo 6 > 5, więc 4 zaokrąglamy do 5, a jedności zastępujemy zerem)
3,14 (bo 1 < 5)
1000 (bo 9 > 5, więc 9 zaokrąglamy do 10, przenosimy 1 do następnej cyfry, itd.)
0,01 (bo 7 > 5, więc 0 zaokrąglamy do 1)

Pułapki i Najczęstsze Błędy

Podczas zaokrąglania łatwo popełnić błędy. Oto kilka najczęstszych pułapek, na które warto uważać:

Zapominanie o miejscu zaokrąglenia: Zawsze upewnij się, do którego miejsca masz zaokrąglić liczbę.
Błędna interpretacja reguły "5 i więcej": Pamiętaj, że 5 zaokrąglamy w górę, a nie w dół.
Zaokrąglanie etapami: Nigdy nie zaokrąglaj liczby kilkukrotnie, tylko raz, do wybranego miejsca. Na przykład, zaokrąglając 3,14159 do części setnych, nie zaokrąglaj najpierw do części tysięcznych, a potem do części setnych.
Ignorowanie zer: Pamiętaj, że zera po przecinku są ważne, szczególnie gdy zaokrąglamy do miejsc po przecinku. Na przykład, 1,00 to co innego niż 1.

Zaokrąglanie w Życiu Codziennym

Zaokrąglanie to umiejętność, która przydaje się nie tylko w szkole, ale i w wielu sytuacjach życiowych. Oto kilka przykładów:

Zakupy: Obliczając koszt zakupów, często zaokrąglamy ceny produktów, aby oszacować całkowity wydatek.
Gotowanie: Dostosowując przepisy, zaokrąglamy proporcje składników, aby ułatwić sobie odmierzanie.
Planowanie podróży: Obliczając czas podróży, zaokrąglamy godziny i minuty, aby mieć ogólny obraz sytuacji.
Finanse: Śledząc swoje wydatki, zaokrąglamy kwoty, aby uprościć analizę budżetu.

Wyobraź sobie, że idziesz do sklepu i kupujesz kilka produktów: chleb za 2,89 zł, masło za 7,15 zł i ser za 12,35 zł. Możesz szybko zaokrąglić te kwoty do 3 zł, 7 zł i 12 zł, aby oszacować, że zapłacisz około 22 zł. To o wiele szybsze niż dokładne dodawanie liczb.

Podsumowanie

Zaokrąglanie liczb to ważna umiejętność, która ułatwia życie i pomaga w podejmowaniu decyzji. Pamiętaj o podstawowych zasadach: określ miejsce zaokrąglenia, obserwuj cyfrę następną i stosuj regułę "5 i więcej – w górę, mniej niż 5 – w dół". Ćwicz regularnie, rozwiązuj zadania i unikaj typowych błędów. Z czasem zaokrąglanie stanie się dla Ciebie naturalne i intuicyjne, a Ty będziesz mógł swobodnie upraszczać obliczenia i prezentować dane w bardziej przejrzysty sposób.

Pamiętaj, że matematyka jest wszędzie wokół nas, a zaokrąglanie to tylko jedno z narzędzi, które pomagają nam ją zrozumieć i wykorzystać w praktyce. Powodzenia!