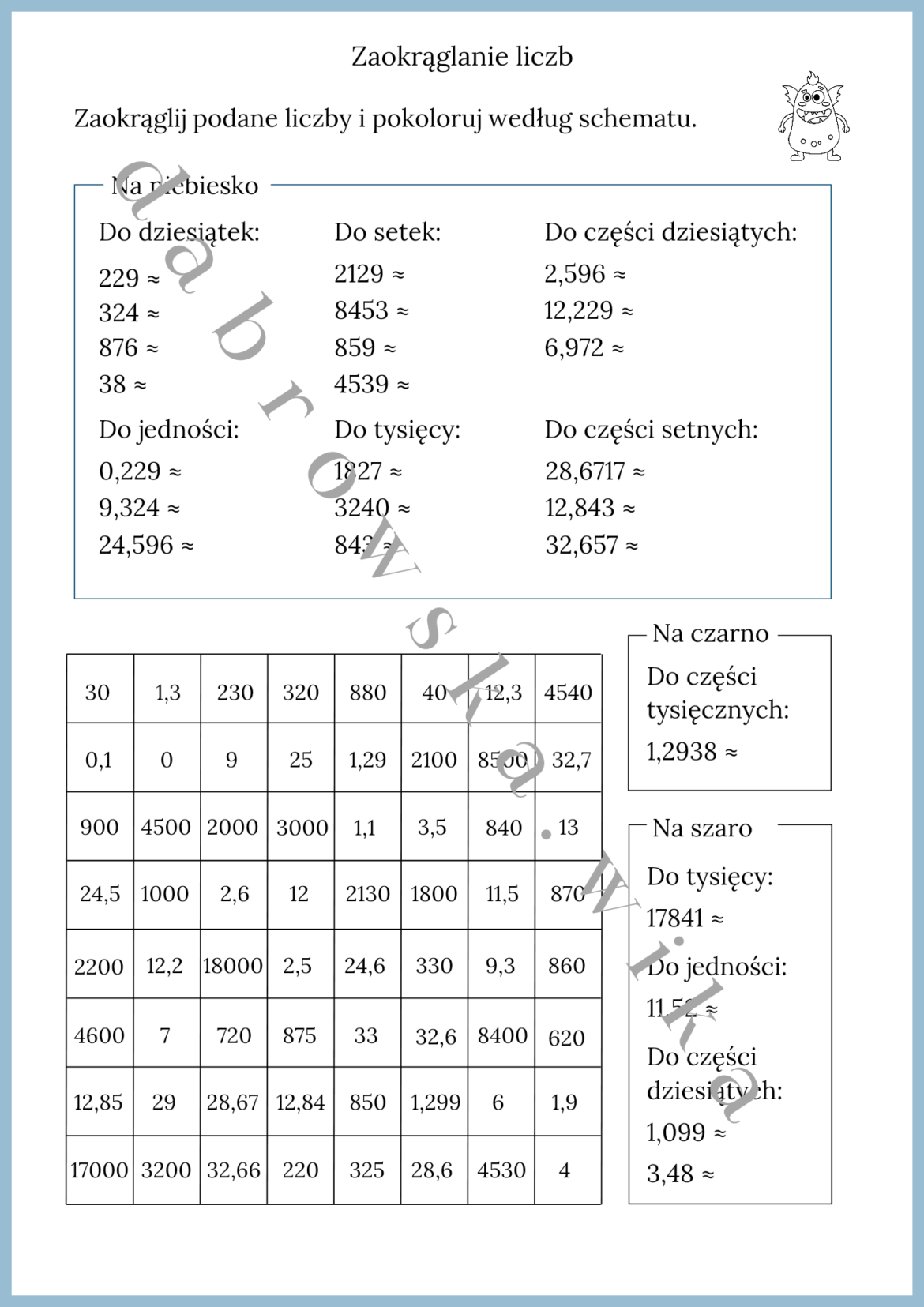
Zaokrąglanie Liczb Do Jedności Dziesiątek Setek I Tysięcy

Zaokrąglanie liczb jest fundamentalną umiejętnością matematyczną, która przydaje się w wielu aspektach życia, od szacowania kosztów zakupów po analizowanie danych statystycznych. W praktyce często operujemy na przybliżonych wartościach, a zaokrąglanie pozwala nam uprościć liczby, zachowując jednocześnie ich istotę. W tym artykule przyjrzymy się, jak zaokrąglać liczby do jedności, dziesiątek, setek i tysięcy, prezentując konkretne przykłady i wskazówki.

Zaczniemy od najprostszego przypadku: zaokrąglania do jedności. Wyobraźmy sobie, że mamy liczbę 3,7. Interesuje nas, do której liczby całkowitej jest ona bliżej. Patrzymy na cyfrę po przecinku, czyli w tym przypadku 7. Ponieważ 7 jest większe lub równe 5, zaokrąglamy liczbę w górę, czyli do 4. Jeśli mielibyśmy liczbę 3,2, to cyfra po przecinku to 2, która jest mniejsza od 5, więc zaokrąglamy w dół, do 3.

Kolejny przykład: 12,49. Cyfra po przecinku to 4, czyli zaokrąglamy w dół, do 12. A co z liczbą 12,51? Tu cyfra po przecinku to 5, więc zaokrąglamy w górę, do 13. Zapamiętajmy: jeśli cyfra po przecinku jest mniejsza od 5, zaokrąglamy w dół; jeśli jest równa lub większa od 5, zaokrąglamy w górę.

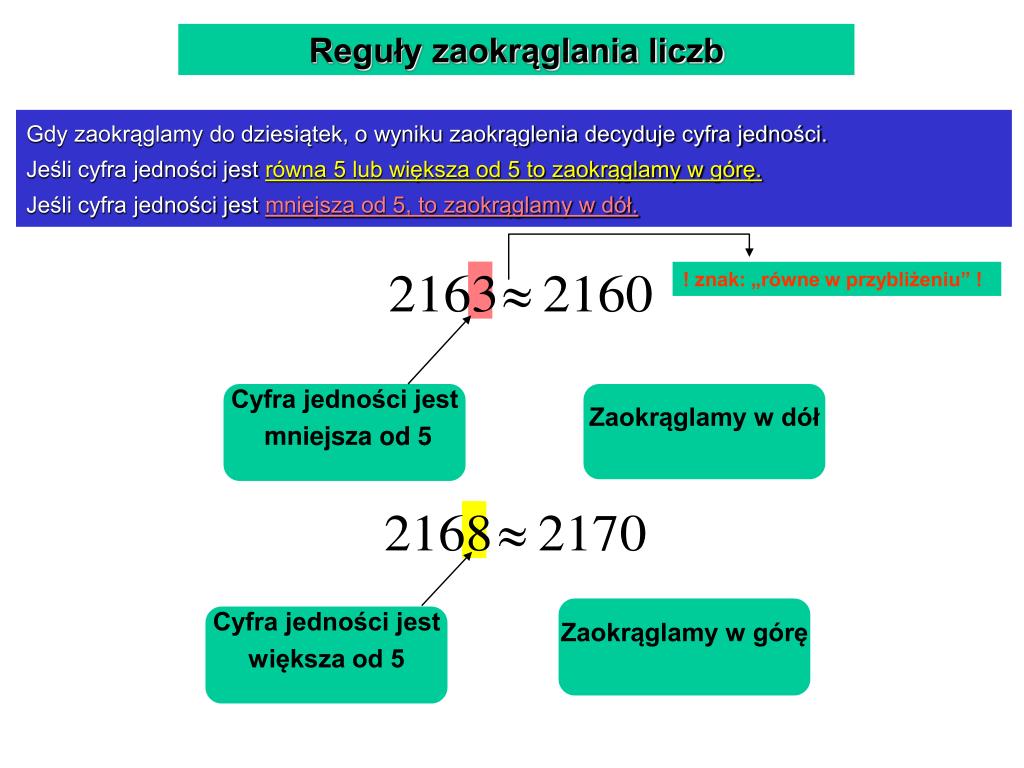
Teraz przejdźmy do zaokrąglania do dziesiątek. Tu już zaczyna się robić nieco bardziej interesująco. Weźmy liczbę 63. Interesuje nas teraz cyfra jedności, czyli 3. Ponieważ 3 jest mniejsze od 5, zaokrąglamy w dół, do 60. Jeśli mamy liczbę 68, to cyfra jedności to 8, która jest większa od 5, więc zaokrąglamy w górę, do 70. Liczba 65 zaokrąglana jest w górę do 70, ponieważ 5 jest równe 5.

Spróbujmy z liczbą trzycyfrową: 127. Patrzymy na cyfrę jedności, czyli 7. Jest ona większa od 5, więc "dodajemy" dziesiątkę do 120, co daje nam 130. A co z liczbą 122? Cyfra jedności to 2, więc zaokrąglamy w dół, do 120.

Bardziej złożony przykład: 354. Patrzymy na 4. Zaokrąglamy w dół do 350. Z kolei 358 zaokrąglamy w górę do 360. Widzimy więc, że zaokrąglanie do dziesiątek sprowadza się do "zerowania" cyfry jedności i ewentualnej korekty cyfry dziesiątek, w zależności od wartości cyfry jedności.

Zaokrąglanie do setek to kolejny krok. Teraz koncentrujemy się na cyfrze dziesiątek. Mamy liczbę 235. Cyfra dziesiątek to 3, która jest mniejsza od 5, więc zaokrąglamy w dół, do 200. Jeśli mamy liczbę 271, cyfra dziesiątek to 7, która jest większa od 5, więc zaokrąglamy w górę, do 300. Liczba 250 zaokrąglana jest w górę do 300.

Rozważmy większą liczbę: 1789. Patrzymy na cyfrę dziesiątek, czyli 8. Zaokrąglamy w górę, co oznacza, że "dodajemy" setkę do 1700, uzyskując 1800. A co z liczbą 1210? Cyfra dziesiątek to 1, więc zaokrąglamy w dół, do 1200.

Ważne jest, aby pamiętać, że zaokrąglamy kolejno. Nie zaokrąglamy najpierw do dziesiątek, a potem wyniku do setek. To prowadzi do błędów. Zawsze patrzymy na cyfrę bezpośrednio mniejszą od tej, do której zaokrąglamy.

Zaokrąglanie do tysięcy działa na tej samej zasadzie, ale teraz patrzymy na cyfrę setek. Mamy liczbę 4321. Cyfra setek to 3, która jest mniejsza od 5, więc zaokrąglamy w dół, do 4000. Jeśli mamy liczbę 4789, cyfra setek to 7, która jest większa od 5, więc zaokrąglamy w górę, do 5000. Liczba 4500 zaokrąglana jest w górę do 5000.

Spójrzmy na większą liczbę: 12876. Cyfra setek to 8, więc zaokrąglamy w górę, co oznacza, że "dodajemy" tysiąc do 12000, uzyskując 13000. A co z liczbą 12100? Cyfra setek to 1, więc zaokrąglamy w dół, do 12000.

Pamiętajmy, że zaokrąglanie to uproszczenie. Tracimy część precyzji, ale zyskujemy czytelność i łatwość operowania na liczbach.

Przykłady Zaokrąglania w Praktyce

Wyobraźmy sobie, że robimy zakupy w sklepie. Nasz koszyk zawiera produkty o następujących cenach: 2,79 zł, 5,25 zł, 12,49 zł i 8,99 zł. Jeśli chcemy szybko oszacować koszt zakupów, możemy zaokrąglić ceny do jedności: 3 zł, 5 zł, 12 zł i 9 zł. Wtedy szacunkowy koszt to 3 + 5 + 12 + 9 = 29 zł.

Inny przykład: analizujemy wyniki sondażu, w którym 567 osób odpowiedziało "tak" na pytanie. Zaokrąglając do setek, możemy powiedzieć, że około 600 osób odpowiedziało "tak". To upraszcza prezentację wyników i ułatwia ich zrozumienie.

Kolejny przykład: firma wygenerowała przychód w wysokości 123456 zł. Zaokrąglając do tysięcy, możemy powiedzieć, że firma zarobiła około 123 tysiące złotych.

Pułapki i Wskazówki

Podczas zaokrąglania liczb warto unikać kilku pułapek. Po pierwsze, jak już wspomniano, nie zaokrąglajmy pośrednich wyników. Zawsze zaokrąglajmy dopiero wynik końcowy. Po drugie, zastanówmy się, do jakiej dokładności potrzebujemy zaokrąglić. Czy wystarczy zaokrąglić do jedności, czy potrzebujemy większej precyzji i zaokrąglamy do dziesiątek lub setek?

Po trzecie, pamiętajmy o kontekście. W niektórych sytuacjach, np. w obliczeniach finansowych, nawet niewielkie różnice wynikające z zaokrąglania mogą mieć znaczący wpływ na wynik końcowy. W takich przypadkach warto zachować większą precyzję i zaokrąglać dopiero na samym końcu obliczeń.

Po czwarte, warto stosować reguły zaokrąglania konsekwentnie. Używanie różnych metod zaokrąglania w różnych częściach obliczeń może prowadzić do niespójnych wyników.

Podsumowując, zaokrąglanie liczb to prosta, ale potężna umiejętność, która ułatwia nam operowanie na liczbach i szacowanie wartości. Pamiętajmy o podstawowych zasadach i unikajmy typowych błędów, a zaokrąglanie stanie się naszym sprzymierzeńcem w codziennych obliczeniach.