Zamień Ułamek Na Liczbę Mieszaną

Czy kiedykolwiek patrzyłeś na ułamek, taki jak ¹¹/₄, i czułeś się trochę zagubiony? Nie jesteś sam! Wiele osób, zwłaszcza tych zaczynających przygodę z matematyką, ma trudności z interpretacją ułamków niewłaściwych i ich powiązaniem z liczbami mieszanymi. Często wydaje się to skomplikowane, ale obiecuję, że zamiana ułamka na liczbę mieszaną jest prostsza niż myślisz.

Zrozumiem, jeśli uważasz, że to "tylko matematyka". Jednak ułamki i liczby mieszane są wszechobecne w życiu codziennym. Wyobraź sobie, że pieczesz ciasto i przepis wymaga 2 ¹/₂ szklanki mąki. Co to dokładnie oznacza? A może dzielisz pizzę ze znajomymi i zostaje ⁷/₃ pizzy. Jak podzielić ją sprawiedliwie? Zrozumienie, jak zamieniać ułamki na liczby mieszane, pozwala nam praktycznie stosować matematykę w realnych sytuacjach.

Dlaczego Warto Umieć Zamieniać Ułamki na Liczby Mieszane?

• Łatwiejsza interpretacja: Liczba mieszana, np. 1 ¹/₂, jest bardziej intuicyjna niż ułamek niewłaściwy ³/₂. Od razu widzisz, że masz "całą jedynkę" i "pół".
• Praktyczne zastosowanie: Jak wspomniałem wcześniej, w kuchni, w budownictwie, a nawet w finansach często spotykamy się z liczbami mieszanymi.
• Ułatwienie obliczeń: W niektórych przypadkach, szczególnie przy dodawaniu i odejmowaniu, operowanie na liczbach mieszanych jest prostsze niż na ułamkach niewłaściwych.

Ułamki Niewłaściwe kontra Liczby Mieszane – Czym się Różnią?

Zacznijmy od podstaw. Ułamek niewłaściwy to taki ułamek, w którym licznik (górna liczba) jest większy lub równy mianownikowi (dolna liczba). Przykłady: ⁵/₂, ⁷/₃, ⁴/₄.

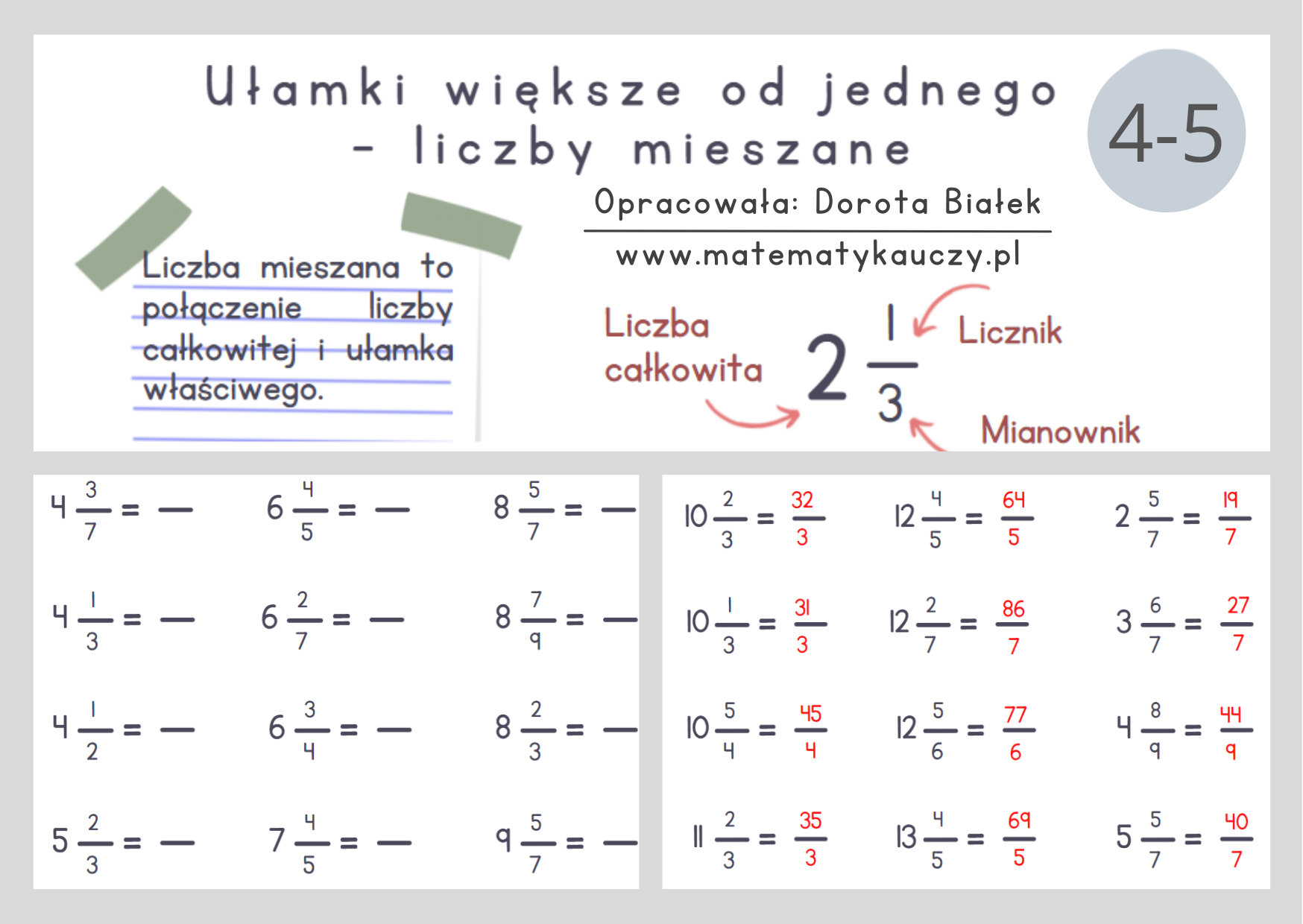
Liczba mieszana to połączenie liczby całkowitej i ułamka właściwego. Przykłady: 2 ¹/₂, 1 ¹/₃.

Zasadniczo, ułamek niewłaściwy reprezentuje ilość większą niż 1, a liczba mieszana to po prostu inny sposób zapisania tej samej ilości.

Krok po Kroku: Jak Zamienić Ułamek na Liczbę Mieszaną

1. Podziel licznik przez mianownik. Wykonaj dzielenie z resztą. Na przykład, dla ułamka ¹¹/₄ dzielimy 11 przez 4.
2. Ustal liczbę całkowitą. Liczba całkowita w liczbie mieszanej to wynik dzielenia (bez reszty). W naszym przykładzie, 11 podzielone przez 4 daje 2 (z resztą). Zatem, liczba całkowita to 2.
3. Ustal licznik ułamka. Licznik ułamka to reszta z dzielenia. W naszym przykładzie, reszta z dzielenia 11 przez 4 to 3. Zatem, licznik ułamka to 3.
4. Ustal mianownik ułamka. Mianownik ułamka pozostaje taki sam jak mianownik oryginalnego ułamka. W naszym przykładzie, mianownik to 4.
5. Zapisz liczbę mieszaną. Połącz liczbę całkowitą, licznik ułamka i mianownik ułamka. W naszym przykładzie, ¹¹/₄ zamienia się na 2 ³/₄.

Przykład: Zamiana ¹⁷/₅ na Liczbę Mieszaną

1. Dzielimy 17 przez 5.
2. Wynik dzielenia to 3 (z resztą). Zatem, liczba całkowita to 3.
3. Reszta z dzielenia to 2. Zatem, licznik ułamka to 2.
4. Mianownik ułamka to 5.
5. Zatem, ¹⁷/₅ = 3 ²/₅.

Inny Przykład: Zamiana ²³/₇ na Liczbę Mieszaną

1. Dzielimy 23 przez 7.
2. Wynik dzielenia to 3 (z resztą). Zatem, liczba całkowita to 3.
3. Reszta z dzielenia to 2. Zatem, licznik ułamka to 2.
4. Mianownik ułamka to 7.
5. Zatem, ²³/₇ = 3 ²/₇.

Potencjalne Pułapki i Jak Ich Unikać

Błąd: Zapominanie o reszcie. Upewnij się, że uwzględniasz resztę z dzielenia przy tworzeniu ułamka w liczbie mieszanej.

Rozwiązanie: Zawsze sprawdzaj, czy licznik w ułamku w liczbie mieszanej jest mniejszy niż mianownik. Jeśli nie, popełniłeś błąd!

Błąd: Mylenie licznika i mianownika w ułamku w liczbie mieszanej.

Rozwiązanie: Pamiętaj, że mianownik pozostaje taki sam! Licznik ułamka w liczbie mieszanej to reszta z dzielenia.

Błąd: Nie upraszczanie ułamka w liczbie mieszanej.

Rozwiązanie: Zawsze upewnij się, że ułamek w liczbie mieszanej jest w najprostszej postaci. Na przykład, jeśli otrzymasz 2 ²/₄, uprość to do 2 ¹/₂.

Argumenty Przeciwne: Czy Zamiana Ułamków na Liczby Mieszane Jest Zawsze Konieczna?

Niektórzy twierdzą, że w pewnych sytuacjach (np. przy bardziej zaawansowanych obliczeniach algebraicznych) operowanie na ułamkach niewłaściwych jest prostsze. I to prawda! Czasami wygodniej jest pracować z ⁵/₂ niż z 2 ¹/₂, zwłaszcza przy mnożeniu i dzieleniu ułamków.

Jednak dla zrozumienia wartości ułamka oraz w wielu praktycznych sytuacjach, zamiana na liczbę mieszaną jest bardzo pomocna. Ostatecznie, umiejętność wykonywania obu operacji – zamiany ułamka na liczbę mieszaną i odwrotnie – jest kluczowa dla elastycznego i skutecznego posługiwania się ułamkami.

Kiedy Zamiana Ułamka na Liczbę Mieszaną Jest Szczególnie Przydatna?

• Gotowanie i pieczenie: Jak już wspomniałem, przepisy często używają liczb mieszanych do określania ilości składników.
• Stolarstwo i budownictwo: Przy cięciu materiałów, takich jak drewno, często mierzy się długości w ułamkach cala, które są łatwiej zrozumiałe jako liczby mieszane.
• Mierzenie czasu: Na przykład, 1 ¹/₂ godziny to proste do zrozumienia "półtorej godziny".
• Dzielenie zasobów: Jeśli masz ¹³/₄ pizzy, łatwiej jest zrozumieć, że masz 3 całe pizze i jeszcze ćwiartkę, co ułatwia sprawiedliwe podzielenie.

Podsumowanie i Dalsze Kroki

Mam nadzieję, że teraz czujesz się pewniej w temacie zamiany ułamków na liczby mieszane. Pamiętaj, kluczem jest praktyka. Ćwicz na różnych przykładach, a zobaczysz, że to staje się coraz łatwiejsze.

Uproszczenie wizualne: Wyobraź sobie, że ułamek to tort pokrojony na kawałki. Ułamek niewłaściwy to więcej kawałków niż potrzebne do ułożenia całego tortu. Liczba mieszana to całe torty i pozostałe kawałki.

Pamiętaj o kluczowych krokach: Dziel, znajdź resztę, utwórz ułamek z reszty i mianownika, a następnie zapisz liczbę mieszaną.

Czy jesteś gotów, aby samodzielnie poćwiczyć? Wybierz kilka ułamków niewłaściwych i spróbuj zamienić je na liczby mieszane. Sprawdź swoje odpowiedzi online lub poproś kogoś o sprawdzenie. Z każdym kolejnym przykładem będziesz coraz lepszy! Powodzenia!

Co sprawia Ci największą trudność w pracy z ułamkami? Z jakimi problemami spotykasz się najczęściej? Podziel się swoimi pytaniami i przemyśleniami w komentarzach poniżej!