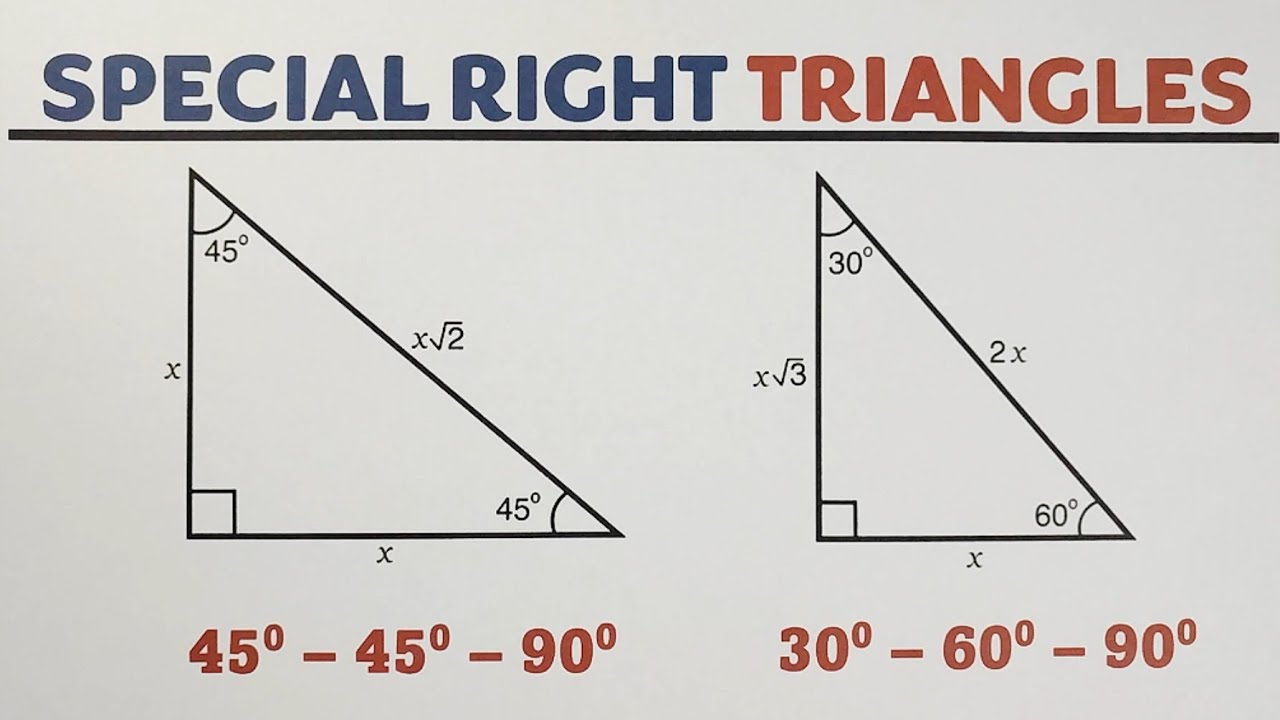
Zależności W Trójkącie 45 45 90

W geometrii, niektóre figury, a zwłaszcza trójkąty, charakteryzują się szczególnymi właściwości, które ułatwiają obliczenia i analizę. Jednym z takich wyjątkowych trójkątów jest trójkąt prostokątny równoramienny, często nazywany trójkątem 45-45-90. Jego unikalne proporcje, wynikające z kątów o miarach 45°, 45° i 90°, sprawiają, że znajomość zależności w nim panujących jest niezwykle przydatna w różnych dziedzinach – od matematyki i fizyki, po architekturę i inżynierię.

Kluczowe zależności w trójkącie 45-45-90

Podstawą analizy tego trójkąta jest zrozumienie jego budowy i wynikających z niej relacji. Trójkąt 45-45-90, jak sama nazwa wskazuje, jest trójkątem prostokątnym (posiada kąt prosty) oraz równoramiennym (dwa boki są równej długości).

Równość boków i kątów

Fakt, że trójkąt jest równoramienny, oznacza, że dwa kąty przy podstawie (kąty leżące naprzeciwko równych boków) muszą być równe. W trójkącie prostokątnym suma wszystkich kątów wynosi 180°. Ponieważ jeden z kątów ma miarę 90°, pozostałe dwa muszą razem mieć 90°. Skoro są one równe, to każdy z nich ma miarę 45°.

Niech a oznacza długość każdego z ramion (przyprostokątnych) trójkąta 45-45-90. Wówczas, zgodnie z twierdzeniem Pitagorasa, długość przeciwprostokątnej (boku leżącego naprzeciwko kąta prostego) można obliczyć następująco:

a² + a² = c²

2a² = c²

c = √(2a²) = a√2

Zatem, przeciwprostokątna ma długość a√2, gdzie a to długość każdego z ramion. Jest to kluczowa zależność, którą warto zapamiętać.

Zależność między polem a bokiem

Pole trójkąta prostokątnego można obliczyć jako połowę iloczynu długości jego przyprostokątnych. W trójkącie 45-45-90, obie przyprostokątne mają długość a. Zatem:

Pole = (1/2) * a * a = (1/2)a²

Znając długość ramienia (przyprostokątnej), łatwo obliczyć pole trójkąta i vice versa. Jeżeli znamy pole trójkąta P, to długość ramienia a wynosi:

a = √(2P)

Funkcje trygonometryczne dla kąta 45°

Trójkąt 45-45-90 jest doskonałym przykładem do ilustracji funkcji trygonometrycznych dla kąta 45°. Korzystając z definicji funkcji sinus, cosinus i tangens:

Wartości te są podstawowe i często wykorzystywane w rozwiązywaniu zadań z trygonometrii.

Przykłady zastosowań w praktyce

Zależności w trójkącie 45-45-90 znajdują szerokie zastosowanie w różnych dziedzinach życia.

Architektura i Budownictwo

W architekturze, trójkąty 45-45-90 są wykorzystywane do projektowania konstrukcji, w których istotne jest zachowanie kątów prostych i symetrii. Przykładem może być projektowanie dachów o kącie nachylenia 45°, gdzie znajomość długości ramion trójkąta (wysokości i szerokości dachu) pozwala na szybkie obliczenie długości krokwi (przeciwprostokątnej). Również projektowanie schodów, w których kąt nachylenia wynosi 45 stopni, wykorzystuje te same zależności.

Inżynieria

W inżynierii, trójkąty 45-45-90 mogą być używane do obliczania odległości i wysokości w terenie. Na przykład, jeśli wiemy, że kąt wzniesienia celownika jest równy 45°, a odległość od obserwatora do punktu pod obiektem wynosi a, to wysokość obiektu również wynosi a. To proste spostrzeżenie jest przydatne w geodezji i kartografii.

Geometria i Matematyka

Trójkąty 45-45-90 pojawiają się w wielu zadaniach z geometrii, zarówno w szkole podstawowej, jak i na poziomie uniwersyteckim. Często są one elementem bardziej złożonych figur geometrycznych, a znajomość zależności w nich panujących pozwala na uproszczenie obliczeń. Na przykład, w zadaniach dotyczących kwadratów i ich przekątnych, trójkąty 45-45-90 odgrywają kluczową rolę, ponieważ przekątna kwadratu dzieli go na dwa takie trójkąty.

Konstrukcja narzędzi i sprzętów

W procesie produkcyjnym różnych narzędzi i sprzętów, precyzja kątów jest często kluczowa. Trójkąty 45-45-90 mogą być wykorzystywane jako wzorce do sprawdzania kątów prostych i kątów 45°. Wiele narzędzi, takich jak kątowniki, bazuje na tej geometrii.

Grafika komputerowa i gry wideo

W grafice komputerowej i tworzeniu gier wideo, znajomość zależności w trójkącie 45-45-90 jest przydatna do obliczania odległości i kierunków, zwłaszcza w prostych systemach graficznych. Obiekty poruszające się pod kątem 45 stopni względem osi współrzędnych mogą być łatwo modelowane z wykorzystaniem tych zależności.

Przykładowe zadania i rozwiązania

Zadanie 1: Dany jest trójkąt 45-45-90, którego ramię ma długość 5 cm. Oblicz długość przeciwprostokątnej.

Rozwiązanie:

Przeciwprostokątna = a√2 = 5√2 cm

Zadanie 2: Dany jest trójkąt 45-45-90, którego przeciwprostokątna ma długość 10 cm. Oblicz długość ramienia.

Rozwiązanie:

a√2 = 10

a = 10/√2 = (10√2)/2 = 5√2 cm

Zadanie 3: Oblicz pole trójkąta 45-45-90, którego ramię ma długość 4 cm.

Rozwiązanie:

Pole = (1/2)a² = (1/2) * 4² = (1/2) * 16 = 8 cm²

Podsumowanie i wezwanie do działania

Trójkąt 45-45-90 to figura o wyjątkowych właściwościach, które wynikają z jego specyficznej budowy. Znajomość zależności między bokami i kątami w tym trójkącie jest niezwykle przydatna w wielu dziedzinach, od matematyki i fizyki, po architekturę i inżynierię.

Zapamiętaj, że przeciwprostokątna ma długość a√2, gdzie a to długość ramienia. Ćwicz rozwiązywanie zadań, aby utrwalić wiedzę i z łatwością wykorzystywać ją w praktycznych sytuacjach.

Zachęcamy do dalszego zgłębiania wiedzy z geometrii i eksplorowania innych interesujących figur geometrycznych. Matematyka kryje w sobie wiele fascynujących tajemnic! Spróbuj znaleźć więcej przykładów zastosowań trójkąta 45-45-90 w swoim otoczeniu. Zobaczysz, że są one wszędzie!