Zależności W Trójkącie 30 60 90

Czy kiedykolwiek zastanawiałeś się, jak szybko obliczyć długości boków w trójkącie prostokątnym, znając tylko jeden bok i kąt? Istnieją pewne trójkąty, które rządzą się specjalnymi prawami, a jednym z nich jest trójkąt o kątach 30, 60 i 90 stopni. Ten artykuł jest przeznaczony dla uczniów szkół średnich, studentów oraz wszystkich osób zainteresowanych geometrią, które chcą zgłębić zależności występujące w tym szczególnym trójkącie i wykorzystać je w praktyce. Przyjrzymy się bliżej tym relacjom, nauczymy się je rozpoznawać i stosować, co znacznie ułatwi rozwiązywanie zadań geometrycznych.

Czym jest trójkąt 30-60-90?

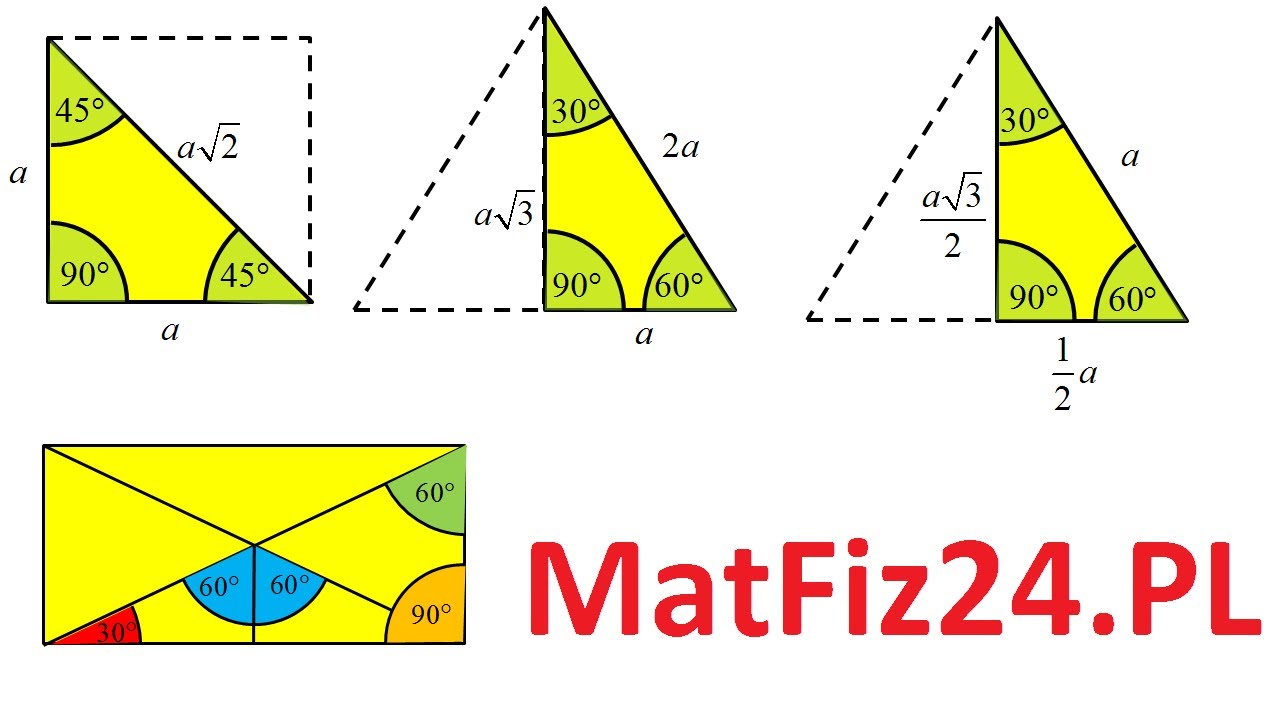
Trójkąt 30-60-90, jak sama nazwa wskazuje, to trójkąt prostokątny, którego kąty wewnętrzne mają miary 30°, 60° i 90°. To ważne, aby pamiętać, że suma kątów w każdym trójkącie wynosi 180°. Dzięki tej specyficznej kombinacji kątów, długości jego boków są powiązane prostymi zależnościami.

Charakterystyczne cechy trójkąta 30-60-90:

Jeden kąt prosty (90°).
Jeden kąt o mierze 30°.
Jeden kąt o mierze 60°.
Stosunek długości boków jest stały i wynosi 1 : √3 : 2.

Zależności między bokami trójkąta 30-60-90

Kluczowym elementem zrozumienia trójkąta 30-60-90 jest poznanie zależności między długościami jego boków. Oznaczmy:

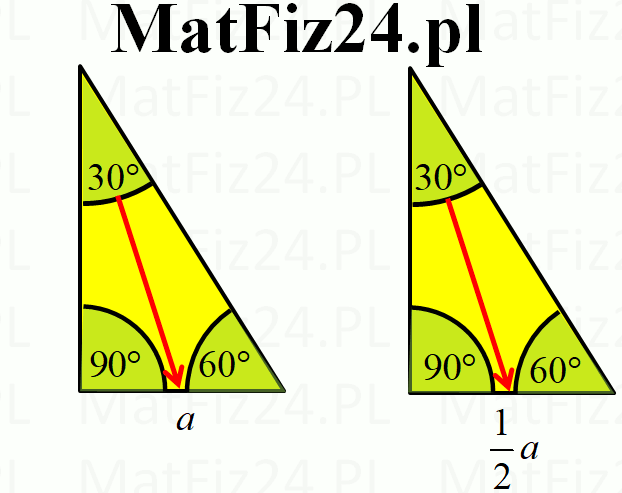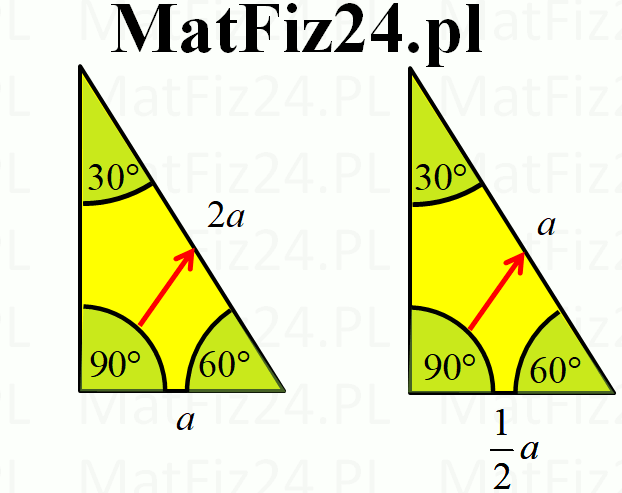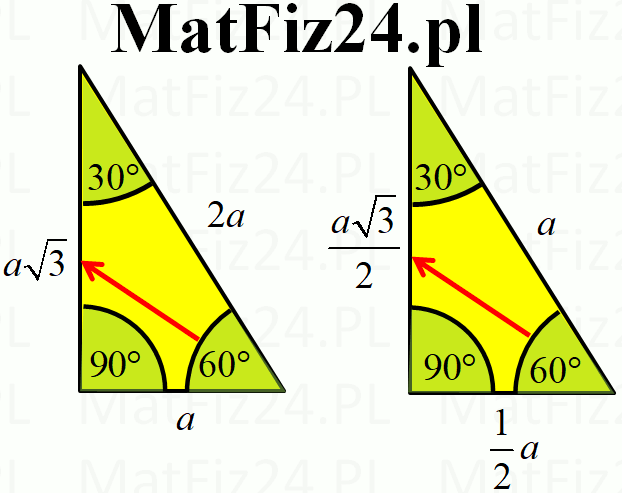
Najkrótszy bok (naprzeciw kąta 30°) jako a.
Bok średniej długości (naprzeciw kąta 60°) jako b.
Najdłuższy bok, czyli przeciwprostokątną (naprzeciw kąta 90°) jako c.

Wówczas zachodzą następujące zależności:

b = a√3 (bok naprzeciw kąta 60° jest √3 razy dłuższy od boku naprzeciw kąta 30°)
c = 2a (przeciwprostokątna jest 2 razy dłuższa od boku naprzeciw kąta 30°)
a = c/2 (bok naprzeciw kąta 30° jest połową długości przeciwprostokątnej)
b = (c√3)/2 (bok naprzeciw kąta 60° jest (√3)/2 długości przeciwprostokątnej)

Te zależności są fundamentem do rozwiązywania problemów związanych z trójkątami 30-60-90. Pamiętając je, możemy szybko obliczyć długości brakujących boków, znając tylko jeden.

Jak rozpoznać trójkąt 30-60-90?

Rozpoznanie trójkąta 30-60-90 jest kluczowe do zastosowania odpowiednich zależności. Najprostszym sposobem jest oczywiście sprawdzenie miar kątów wewnętrznych. Jeśli trójkąt prostokątny ma kąt o mierze 30° (lub 60°), to możemy być pewni, że jest to trójkąt 30-60-90.

Możemy go również rozpoznać, analizując długości boków. Jeśli wiemy, że trójkąt jest prostokątny, a długość jednego z boków (przyprostokątnej) jest połową długości przeciwprostokątnej, to mamy do czynienia z trójkątem 30-60-90. Podobnie, jeśli jeden bok jest √3 razy dłuższy od drugiego (krótszego), również mamy do czynienia z trójkątem 30-60-90.

Przykłady rozpoznawania trójkąta 30-60-90:

Trójkąt o kątach 90°, 30° i 60°.
Trójkąt prostokątny, w którym przeciwprostokątna ma długość 10 cm, a jedna z przyprostokątnych 5 cm.
Trójkąt prostokątny, w którym jedna przyprostokątna ma długość 4 cm, a druga 4√3 cm.

Przykłady zastosowania zależności w praktyce

Zobaczmy, jak możemy wykorzystać te zależności w konkretnych przykładach:

Przykład 1:

Mamy trójkąt 30-60-90, w którym bok naprzeciw kąta 30° ma długość 5 cm. Oblicz długości pozostałych boków.

Rozwiązanie:

a = 5 cm
b = a√3 = 5√3 cm
c = 2a = 2 * 5 = 10 cm

Przykład 2:

Przeciwprostokątna w trójkącie 30-60-90 ma długość 12 cm. Oblicz długości przyprostokątnych.

Rozwiązanie:

c = 12 cm
a = c/2 = 12/2 = 6 cm
b = (c√3)/2 = (12√3)/2 = 6√3 cm

Przykład 3:

Bok naprzeciw kąta 60° w trójkącie 30-60-90 ma długość 7√3 cm. Oblicz długości pozostałych boków.

Rozwiązanie:

b = 7√3 cm
a = b/√3 = (7√3)/√3 = 7 cm
c = 2a = 2 * 7 = 14 cm

Ćwiczenie czyni mistrza! Spróbuj rozwiązać więcej zadań samodzielnie, aby utrwalić zdobytą wiedzę.

Praktyczne zastosowania trójkąta 30-60-90

Trójkąt 30-60-90 ma szerokie zastosowanie w różnych dziedzinach, od matematyki i fizyki po inżynierię i architekturę. Oto kilka przykładów:

Trygonometria: Trójkąt 30-60-90 jest często używany do definiowania wartości funkcji trygonometrycznych dla kątów 30° i 60°.
Geometria: Wykorzystywany do obliczania pól i obwodów figur geometrycznych, które zawierają trójkąty 30-60-90 (np. sześciokąty foremne).
Fizyka: Pomocny w analizie składowych sił i prędkości w zadaniach z mechaniki.
Inżynieria i Architektura: Stosowany w projektowaniu konstrukcji budowlanych, obliczaniu nachyleń i odległości.
Nawigacja: W wykorzystywany w prostych obliczeniach związanych z trasami i odległościami, zwłaszcza przy użyciu kompasu i mapy.

Wskazówki i triki

Oto kilka przydatnych wskazówek, które pomogą Ci w rozwiązywaniu zadań z trójkątami 30-60-90:

Zacznij od rysunku: Zawsze narysuj trójkąt i oznacz znane wartości. Pomoże Ci to wizualizować problem.
Zapamiętaj zależności: Znajomość zależności między bokami jest kluczowa. Staraj się je zapamiętać i zrozumieć, a nie tylko wkuć na pamięć.
Zidentyfikuj najkrótszy bok: Często zadanie polega na znalezieniu długości najkrótszego boku (naprzeciw kąta 30°), ponieważ od niego zależą długości pozostałych boków.
Sprawdź jednostki: Upewnij się, że wszystkie długości są wyrażone w tych samych jednostkach.
Uprość pierwiastki: Jeśli wynik zawiera pierwiastek, spróbuj go uprościć.

Podsumowanie

Trójkąt 30-60-90 to niezwykle użyteczne narzędzie w rozwiązywaniu problemów geometrycznych i trygonometrycznych. Zrozumienie zależności między jego bokami pozwala na szybkie i efektywne obliczanie brakujących wartości. Pamiętając o tych relacjach, będziesz w stanie z łatwością rozwiązywać zadania, które wcześniej wydawały się skomplikowane. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć istotę i zastosowanie trójkąta 30-60-90. Teraz, uzbrojony w tę wiedzę, jesteś gotów, aby zmierzyć się z kolejnymi wyzwaniami matematycznymi!