Zakres Materiału Egzamin ósmoklasisty Matematyka 2021

Kochani Uczniowie Klas Ósmych!

Zbliża się egzamin ósmoklasisty z matematyki w 2021 roku. Wiem, że stres i obawy są naturalne, ale pamiętajcie, że gruntowna wiedza i systematyczna praca to klucz do sukcesu. Postaram się Wam w prosty sposób przybliżyć zakres materiału, którego możecie się spodziewać. Skupimy się na najważniejszych zagadnieniach i podpowiem, na co zwrócić szczególną uwagę podczas powtórek.

Liczby i Działania

Zaczynamy od podstaw, czyli od liczb. Musimy znać różne rodzaje liczb: naturalne (1, 2, 3…), całkowite (…-2, -1, 0, 1, 2…), wymierne (czyli takie, które można zapisać w postaci ułamka zwykłego, np. 1/2, -3/4, 5) i niewymierne (takie, których nie da się zapisać w postaci ułamka zwykłego, np. √2, π).

Ważne jest, aby sprawnie wykonywać działania na liczbach – dodawanie, odejmowanie, mnożenie i dzielenie. Pamiętajcie o kolejności wykonywania działań: najpierw nawiasy, potem potęgowanie i pierwiastkowanie, następnie mnożenie i dzielenie, a na końcu dodawanie i odejmowanie. Ćwiczcie obliczenia, korzystając z różnych przykładów i zadań.

Ułamki to temat, który często sprawia trudności. Przypomnijcie sobie, jak sprowadzać ułamki do wspólnego mianownika, jak dodawać, odejmować, mnożyć i dzielić ułamki zwykłe i dziesiętne. Umiejętność zamiany ułamka zwykłego na dziesiętny i odwrotnie również jest bardzo przydatna.

Procenty to kolejny istotny element. Trzeba umieć obliczać procent danej liczby, jakim procentem jednej liczby jest druga liczba, oraz obliczać liczbę, gdy dany jest jej procent. Nauczcie się rozpoznawać różne rodzaje zadań z procentami i stosować odpowiednie wzory.

Potęgi i pierwiastki to także ważny temat. Przypomnijcie sobie prawa działań na potęgach (np. mnożenie potęg o tej samej podstawie, dzielenie potęg o tej samej podstawie, potęgowanie potęgi) oraz własności pierwiastków (np. pierwiastek z iloczynu, pierwiastek z ilorazu). Warto poćwiczyć upraszczanie wyrażeń z potęgami i pierwiastkami.

Wartości bezwzględne – pamiętajcie, że wartość bezwzględna liczby to jej odległość od zera na osi liczbowej. Czyli wartość bezwzględna z liczby dodatniej jest tą samą liczbą, a wartość bezwzględna z liczby ujemnej jest jej liczbą przeciwną. Trzeba umieć obliczać wartości bezwzględne oraz rozwiązywać proste równania i nierówności z wartością bezwzględną.

Algebra i Równania

Teraz przejdźmy do algebry. Trzeba znać pojęcie wyrażenia algebraicznego, czyli wyrażenia, w którym występują liczby, litery (zmienne) i znaki działań. Umiejętność upraszczania wyrażeń algebraicznych, czyli redukcji wyrazów podobnych, jest bardzo ważna.

Równania to temat, który pojawia się na egzaminie bardzo często. Nauczcie się rozwiązywać równania liniowe z jedną niewiadomą, czyli równania, w których niewiadoma występuje w pierwszej potędze. Pamiętajcie, że rozwiązując równanie, dążymy do tego, aby po jednej stronie równania została sama niewiadoma, a po drugiej stronie – liczba.

Nierówności rozwiązuje się bardzo podobnie do równań, z jedną ważną różnicą: jeśli mnożymy lub dzielimy obie strony nierówności przez liczbę ujemną, to zmieniamy znak nierówności na przeciwny.

Układy równań to dwa lub więcej równań, które rozwiązujemy jednocześnie. Trzeba znać metody rozwiązywania układów równań, np. metodę podstawiania (wyznaczamy jedną niewiadomą z jednego równania i podstawiamy ją do drugiego równania) oraz metodę przeciwnych współczynników (doprowadzamy do tego, aby przy jednej z niewiadomych w obu równaniach stały liczby przeciwne, a następnie dodajemy równania stronami).

Proporcjonalność prosta i odwrotna to kolejne zagadnienie. Proporcjonalność prosta występuje wtedy, gdy dwie wielkości zmieniają się w tym samym kierunku (np. im więcej kupimy towaru, tym więcej zapłacimy). Proporcjonalność odwrotna występuje wtedy, gdy dwie wielkości zmieniają się w przeciwnych kierunkach (np. im szybciej jedziemy, tym krócej trwa podróż). Trzeba umieć rozwiązywać zadania z proporcjonalnością prostą i odwrotną, korzystając z odpowiednich proporcji.

H2 Funkcje

Funkcja to przyporządkowanie, które każdemu elementowi z jednego zbioru (dziedziny) przyporządkowuje dokładnie jeden element z drugiego zbioru (zbioru wartości). Najczęściej spotykamy się z funkcjami, które są określone wzorem lub wykresem.

Trzeba umieć odczytywać informacje z wykresu funkcji, np. dziedzinę, zbiór wartości, miejsca zerowe (czyli punkty, w których wykres przecina oś x), przedziały, w których funkcja rośnie, maleje lub jest stała, wartość funkcji dla danego argumentu.

Szczególnym przypadkiem funkcji jest funkcja liniowa, czyli funkcja postaci y = ax + b, gdzie a i b to liczby. Wykresem funkcji liniowej jest prosta. Trzeba umieć rysować wykres funkcji liniowej, znając jej wzór, oraz wyznaczać wzór funkcji liniowej, znając dwa punkty, które leżą na jej wykresie. Pamiętajcie, że współczynnik a w wzorze funkcji liniowej (czyli liczba stojąca przy x) określa nachylenie prostej do osi x.

Geometria

Przechodzimy do geometrii. Tutaj mamy dwa działy: geometria płaska (czyli figury na płaszczyźnie) i geometria przestrzenna (czyli bryły).

W geometrii płaskiej trzeba znać własności podstawowych figur: trójkątów (równoboczny, równoramienny, prostokątny), czworokątów (kwadrat, prostokąt, równoległobok, romb, trapez) i kół. Trzeba umieć obliczać obwody i pola tych figur. Pamiętajcie o twierdzeniu Pitagorasa, które jest bardzo przydatne przy rozwiązywaniu zadań z trójkątami prostokątnymi.

Symetrie – trzeba umieć rozpoznawać figury symetryczne względem prostej i względem punktu. Pamiętajcie, że figura symetryczna względem prostej to taka figura, która po odbiciu względem tej prostej pokrywa się sama ze sobą. Podobnie, figura symetryczna względem punktu to taka figura, która po obrocie o 180 stopni wokół tego punktu pokrywa się sama ze sobą.

Podobieństwo figur – dwie figury są podobne, jeśli mają taki sam kształt, ale mogą różnić się wielkością. Trzeba umieć obliczać skalę podobieństwa, czyli stosunek długości odpowiadających sobie boków. Pamiętajcie, że stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa.

W geometrii przestrzennej trzeba znać własności podstawowych brył: graniastosłupów (prostopadłościan, sześcian), ostrosłupów, walców, stożków i kul. Trzeba umieć obliczać objętości i pola powierzchni tych brył. Warto nauczyć się rysować siatki graniastosłupów i ostrosłupów.

Statystyka i Kombinatoryka

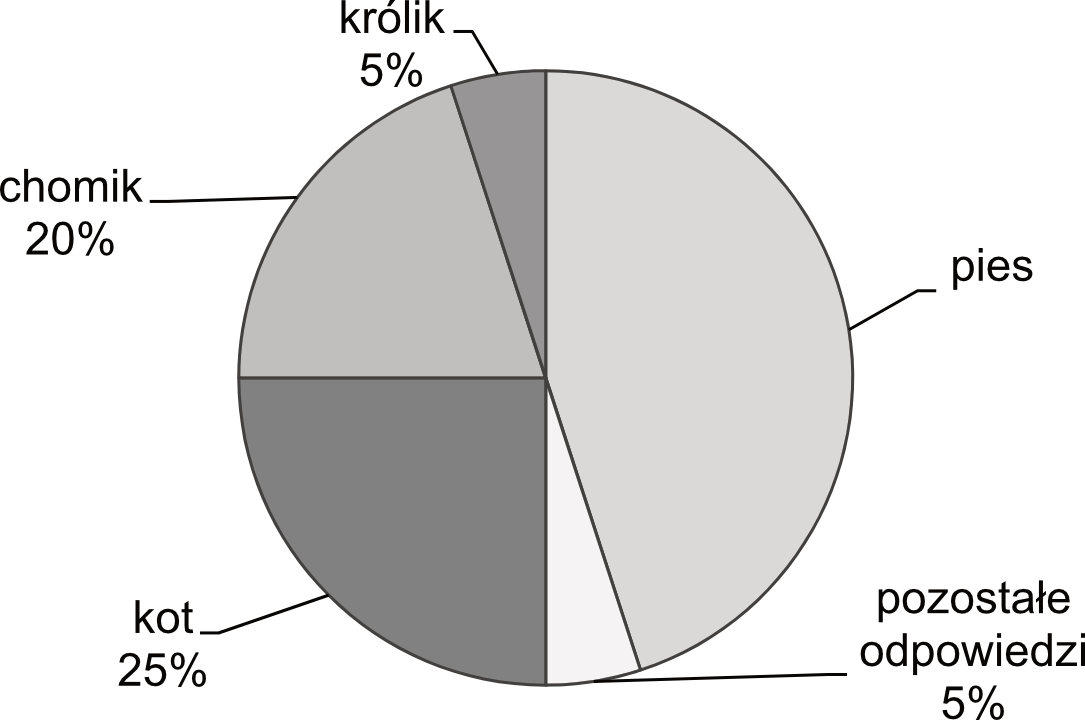
Na koniec – statystyka i kombinatoryka. W statystyce trzeba umieć obliczać średnią arytmetyczną, medianę (czyli wartość środkową w uporządkowanym zbiorze danych) i dominantę (czyli wartość, która występuje najczęściej). Trzeba również umieć interpretować dane przedstawione na wykresach i diagramach.

Kombinatoryka to dział matematyki, który zajmuje się zliczaniem możliwości. Trzeba umieć obliczać liczbę możliwych wyborów, np. liczbę sposobów, na jakie można wybrać k elementów z n-elementowego zbioru.

Prawdopodobieństwo – trzeba umieć obliczać prawdopodobieństwo zdarzeń. Prawdopodobieństwo zdarzenia to stosunek liczby zdarzeń sprzyjających do liczby wszystkich możliwych zdarzeń.

To tylko ogólny zarys materiału, który może pojawić się na egzaminie. Pamiętajcie, że najważniejsze jest systematyczne powtarzanie materiału, rozwiązywanie zadań i analizowanie błędów. Nie bójcie się pytać o to, czego nie rozumiecie. Powodzenia na egzaminie!