Zadania Ze Skali Klasa 7 Geografia

Zrozumienie i umiejętność posługiwania się skalą jest fundamentalną umiejętnością w geografii. Szczególnie w klasie 7, gdzie uczniowie zaczynają bardziej szczegółowo analizować mapy i plany, zadania związane ze skalą nabierają szczególnego znaczenia. Uczniowie mierzą się z przeliczaniem odległości na mapie na odległości w terenie i odwrotnie, a także z interpretacją różnych rodzajów skal. Ten artykuł ma na celu przybliżenie problematyki zadań ze skali, z jakimi spotykają się uczniowie klasy 7, oraz wyjaśnienie kluczowych aspektów związanych z tym zagadnieniem.

Rodzaje Skal i Ich Znaczenie

Istnieją trzy główne rodzaje skal, z którymi uczniowie powinni się zaznajomić:

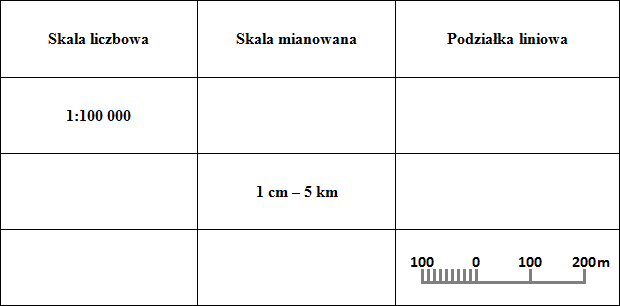
Skala Liczbowa

Skala liczbowa to najczęściej spotykana forma zapisu skali. Wyrażona jest ona za pomocą ułamka, np. 1:100 000. Oznacza to, że 1 jednostka na mapie (np. 1 cm) odpowiada 100 000 takich samych jednostek w terenie (czyli 100 000 cm, co daje 1 km). Ważne jest, aby uczniowie rozumieli, że im mniejszy mianownik ułamka, tym większa skala. Na przykład, skala 1:10 000 jest większa niż skala 1:1 000 000, ponieważ przedstawia obszar bardziej szczegółowo.

Przykład: Jeżeli na mapie w skali 1:50 000 odległość między dwoma miastami wynosi 4 cm, to w rzeczywistości odległość ta wynosi 4 cm * 50 000 = 200 000 cm = 2000 m = 2 km.

Skala Mianowana

Skala mianowana to zapis słowny, np. "1 cm – 5 km". Oznacza on, że 1 centymetr na mapie odpowiada 5 kilometrom w terenie. Jest to bardzo intuicyjna forma zapisu, która ułatwia szybkie przeliczanie odległości bez konieczności wykonywania skomplikowanych obliczeń na ułamkach.

Przykład: Mapa ma skalę mianowaną 1 cm – 10 km. Odległość na mapie między szkołą a parkiem wynosi 2,5 cm. Zatem rzeczywista odległość to 2,5 cm * 10 km/cm = 25 km.

Skala Liniowa (Podziałka Liniowa)

Skala liniowa (podziałka liniowa) to graficzne przedstawienie skali w postaci odcinka podzielonego na równe części, z których każda odpowiada określonej odległości w terenie. Pozwala ona na bezpośredni odczyt odległości w terenie, bez konieczności obliczeń, szczególnie przydatna przy korzystaniu z map drukowanych. Uczniowie powinni umieć nie tylko odczytywać wartości z podziałki, ale także ją konstruować, znając skalę liczbową lub mianowaną.

Przykład: Na mapie znajduje się podziałka liniowa. Odcinek długości 1 cm na podziałce odpowiada 500 metrom w terenie. Mierząc odległość między dwoma punktami na mapie za pomocą cyrkla, a następnie przenosząc tę odległość na podziałkę, możemy odczytać rzeczywistą odległość w terenie.

Przeliczanie Skal

Jednym z kluczowych zadań, z jakimi spotykają się uczniowie, jest przeliczanie skali z jednej formy zapisu na inną. Umiejętność ta jest niezbędna do sprawnego korzystania z map i planów.

Zamiana Skali Liczbowej na Mianowaną

Aby zamienić skalę liczbową na mianowaną, należy przeliczyć mianownik ułamka na bardziej zrozumiałą jednostkę (np. centymetry na kilometry).

Przykład: Skala liczbowa 1:250 000. Oznacza to, że 1 cm na mapie odpowiada 250 000 cm w terenie. Przeliczając 250 000 cm na km, otrzymujemy 2,5 km. Zatem skala mianowana to 1 cm – 2,5 km.

Zamiana Skali Mianowanej na Liczbową

Aby zamienić skalę mianowaną na liczbową, należy doprowadzić do sytuacji, w której zarówno licznik, jak i mianownik ułamka wyrażone są w tych samych jednostkach.

Przykład: Skala mianowana 1 cm – 50 km. 50 km to 50 000 m, a 50 000 m to 5 000 000 cm. Zatem skala liczbowa to 1:5 000 000.

Obliczanie Odległości na Mapie i w Terenie

Najczęściej spotykanym typem zadań jest obliczanie rzeczywistych odległości na podstawie odległości zmierzonych na mapie i odwrotnie.

Obliczanie Odległości w Terenie

Aby obliczyć odległość w terenie, należy pomnożyć odległość zmierzoną na mapie przez mianownik skali (w przypadku skali liczbowej) lub odpowiednią wartość (w przypadku skali mianowanej).

Przykład: Na mapie w skali 1:75 000 odległość między dwoma punktami wynosi 6 cm. Rzeczywista odległość to 6 cm * 75 000 = 450 000 cm = 4500 m = 4,5 km.

Obliczanie Odległości na Mapie

Aby obliczyć odległość na mapie, należy podzielić rzeczywistą odległość przez mianownik skali (w przypadku skali liczbowej) lub odpowiednią wartość (w przypadku skali mianowanej). Należy pamiętać o sprowadzeniu jednostek do wspólnej formy.

Przykład: Rzeczywista odległość między dwoma miejscowościami wynosi 15 km. Mapa ma skalę 1:300 000. 15 km to 1 500 000 cm. Odległość na mapie to 1 500 000 cm / 300 000 = 5 cm.

Zadania Złożone

Często uczniowie spotykają się z zadaniami, które wymagają połączenia kilku umiejętności, np. przeliczenia skali i obliczenia odległości.

Przykład: Na mapie w skali 1:200 000 odległość między punktem A i B wynosi 3 cm. Jaka będzie odległość między tymi punktami na mapie w skali 1:50 000?

Obliczamy rzeczywistą odległość: 3 cm * 200 000 = 600 000 cm = 6 km.
Obliczamy odległość na mapie w skali 1:50 000: 600 000 cm / 50 000 = 12 cm.

Realne Zastosowania

Zrozumienie skali ma praktyczne zastosowanie w wielu sytuacjach życiowych. Pozwala na:

Planowanie podróży z wykorzystaniem map samochodowych i turystycznych.
Orientację w terenie przy użyciu planów miast i map topograficznych.
Analizę danych geograficznych i przestrzennych.
Projektowanie budynków i zagospodarowanie przestrzeni.
Interpretację map w atlasach geograficznych.

Przykład: Planując wycieczkę rowerową, korzystamy z mapy w skali 1:50 000. Chcemy przejechać trasę o długości około 20 km. Na mapie ta trasa będzie miała długość około 40 cm (20 km / (1 km/2 cm) = 40cm). Możemy więc łatwo sprawdzić, czy trasa zmieści się na jednej kartce mapy i czy jest realna do pokonania w ciągu jednego dnia.

Wskazówki i Porady

Aby skutecznie rozwiązywać zadania ze skali, warto pamiętać o kilku ważnych zasadach:

Zawsze sprawdzaj jednostki i upewnij się, że wszystkie wartości są wyrażone w tych samych jednostkach przed wykonaniem obliczeń.
Używaj kalkulatora, aby uniknąć błędów w obliczeniach.
Rysuj schematy i wizualizuj problem, aby lepiej go zrozumieć.
Pracuj na przykładach i rozwiązuj jak najwięcej zadań, aby utrwalić wiedzę.
Pytaj nauczyciela o pomoc, gdy masz trudności.

Pamiętaj! Dokładne wykonywanie pomiarów na mapie jest kluczowe. Używaj linijki, cyrkla, a w przypadku map cyfrowych – dostępnych narzędzi pomiarowych.

Podsumowanie

Zadania ze skali w klasie 7 to istotny element edukacji geograficznej. Opanowanie umiejętności przeliczania skali, obliczania odległości i interpretacji różnych rodzajów skal jest niezbędne do zrozumienia świata, który nas otacza. Pamiętaj, że regularne ćwiczenia i rozwiązywanie różnorodnych zadań to klucz do sukcesu. Powodzenia!