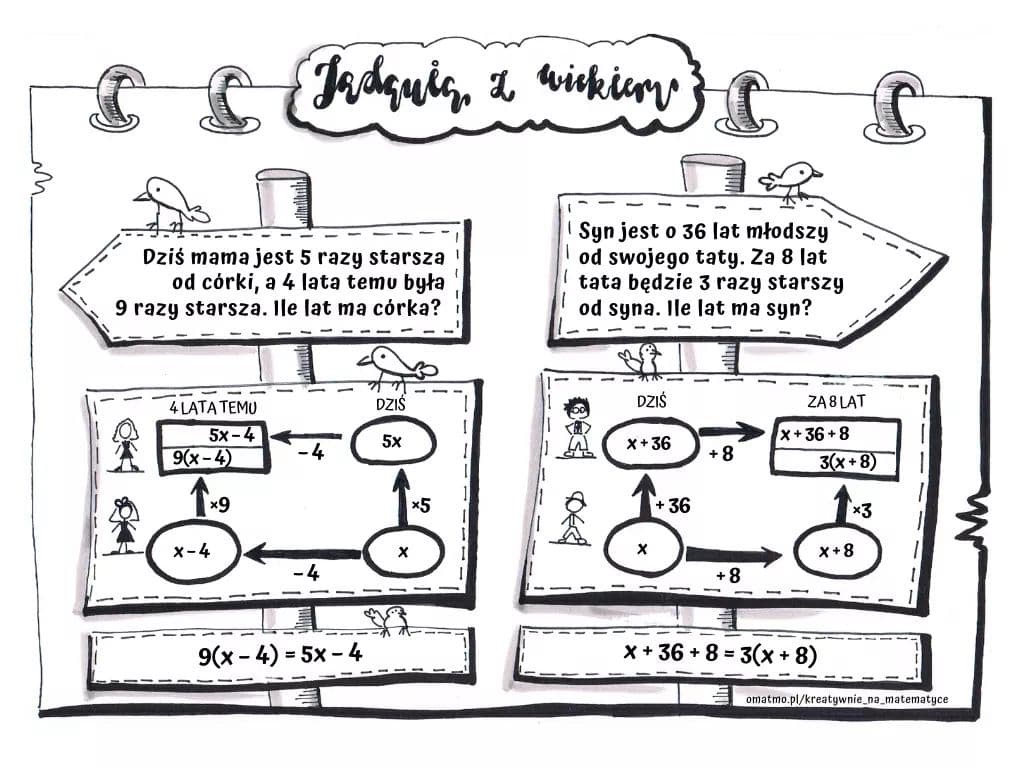
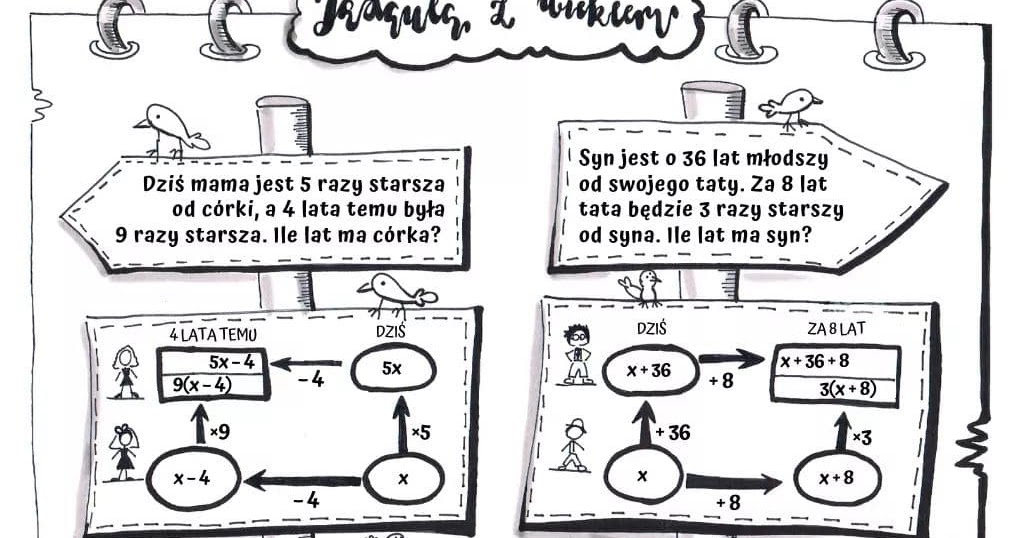
Zadania Z Wiekiem Klasa 8

Czy kiedykolwiek zastanawialiście się, jak rozwiązywać zadania z treścią dotyczące wieku? Te zadania, często spotykane w klasie 8, mogą wydawać się na pierwszy rzut oka skomplikowane, ale z odpowiednią strategią stają się łatwe do pokonania. Ten artykuł jest skierowany do uczniów klasy 8, którzy chcą opanować sztukę rozwiązywania zadań związanych z wiekiem, a także do rodziców i nauczycieli, którzy chcą im w tym pomóc.

Dlaczego Zadania z Wiekiem Są Ważne?

Zadania z wiekiem, choć na pozór dotyczą relacji między osobami w różnym wieku, w rzeczywistości sprawdzają i rozwijają szereg kluczowych umiejętności matematycznych i logicznych. Uczą:

Myślenia algebraicznego: Przekształcania informacji zawartych w treści zadania w równania.
Logicznego wnioskowania: Analizowania i wyciągania wniosków na podstawie danych.
Umiejętności rozwiązywania równań: Opanowania technik rozwiązywania równań liniowych, które są podstawą wielu innych działów matematyki.
Czytania ze zrozumieniem: Dokładnego analizowania treści zadania, wyodrębniania istotnych informacji i pomijania tych zbędnych.
Krytycznego myślenia: Sprawdzania, czy otrzymane rozwiązanie ma sens w kontekście treści zadania.

Te umiejętności są nie tylko przydatne na lekcjach matematyki, ale także w życiu codziennym, gdzie często musimy rozwiązywać problemy, analizować dane i podejmować decyzje na podstawie logicznych przesłanek. Rozwijanie tych umiejętności w klasie 8 przygotowuje was do bardziej zaawansowanych zagadnień matematycznych w przyszłości.

Kluczowe Strategie Rozwiązywania Zadań z Wiekiem

Skuteczne rozwiązywanie zadań z wiekiem opiera się na kilku fundamentalnych strategiach. Pamiętajcie, że praktyka czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie te strategie i tym łatwiej będzie Wam je zastosować w przyszłości.

1. Zrozumienie Treści Zadania

To jest absolutna podstawa. Przeczytaj zadanie uważnie kilka razy. Spróbujcie odpowiedzieć sobie na następujące pytania:

O kogo chodzi w zadaniu? (Kto występuje w zadaniu?)
O jakie relacje wiekowe chodzi? (np. "obecny wiek", "wiek x lat temu", "wiek za y lat")
Co wiemy o tych relacjach? (np. "Jan jest dwa razy starszy od Zosi", "Za pięć lat Maria będzie miała tyle lat, ile Adam ma teraz")
O co nas pytają? (Co mamy obliczyć?)

Podkreślaj ważne informacje w treści zadania. Możesz nawet narysować schemat lub tabelkę, aby uporządkować dane. Im lepiej zrozumiesz treść zadania, tym łatwiej będzie Ci je rozwiązać.

2. Wprowadzenie Oznaczeń

Kolejnym krokiem jest wprowadzenie oznaczeń dla niewiadomych, czyli dla tych wielkości, których wartości musimy obliczyć. Zazwyczaj oznaczamy wiek osób występujących w zadaniu literami. Na przykład:

x – wiek Ani
y – wiek Bartka
z – wiek Celiny

Upewnij się, że wyraźnie określasz, co oznacza każda litera. Na przykład: "x – wiek Ani obecnie". Pamiętaj, że wprowadzenie odpowiednich oznaczeń znacznie ułatwia zapisywanie równań.

3. Ułożenie Równań

Teraz najważniejsza część: ułożenie równań. Przekształć informacje zawarte w treści zadania w język matematyki. Pamiętaj, że słowa takie jak "jest", "będzie", "był" często oznaczają znak równości (=). Na przykład:

"Jan jest dwa razy starszy od Zosi" –> x = 2y (gdzie x to wiek Jana, a y to wiek Zosi)
"Za pięć lat Maria będzie miała tyle lat, ile Adam ma teraz" –> m + 5 = a (gdzie m to obecny wiek Marii, a a to obecny wiek Adama)
"Trzy lata temu Piotr był trzy razy młodszy od swojego taty" --> p - 3 = (t - 3) / 3 (gdzie p to obecny wiek Piotra, a t to obecny wiek taty)

Zazwyczaj potrzebujesz tyle równań, ile masz niewiadomych. Jeśli masz dwie niewiadome (np. wiek Ani i wiek Bartka), potrzebujesz dwóch równań. Jeśli masz trzy niewiadome, potrzebujesz trzech równań i tak dalej.

4. Rozwiązanie Równań

Po ułożeniu równań, kolejnym krokiem jest ich rozwiązanie. Wykorzystaj znane Ci metody rozwiązywania równań liniowych, takie jak:

Metoda podstawiania: Wyrażenie jednej zmiennej za pomocą drugiej z jednego równania i podstawienie tego wyrażenia do drugiego równania.
Metoda przeciwnych współczynników: Pomnożenie równań przez odpowiednie liczby tak, aby przy jednej ze zmiennych otrzymać przeciwne współczynniki, a następnie dodanie równań stronami.

Pamiętaj, aby dokładnie i uważnie wykonywać wszystkie obliczenia. Jeden błąd może zepsuć całe rozwiązanie!

5. Sprawdzenie Rozwiązania

Ostatnim, ale bardzo ważnym krokiem, jest sprawdzenie, czy otrzymane rozwiązanie ma sens w kontekście treści zadania. Odpowiedź na pytanie, czy wiek danej osoby może być ujemny? Albo czy wiek rodzeństwa może różnić się o 50 lat? Czy uzyskane wyniki spełniają wszystkie warunki zadania?

Jeśli rozwiązanie nie spełnia warunków zadania, oznacza to, że popełniłeś błąd w którymś z wcześniejszych kroków i musisz wrócić do początku i spróbować jeszcze raz.

Przykładowe Zadanie z Rozwiązaniem

Zobaczmy, jak te strategie działają w praktyce. Rozważmy następujące zadanie:

Treść zadania: Jan jest dwa razy starszy od Zosi. Sześć lat temu Jan był trzy razy starszy od Zosi. Ile lat ma Jan, a ile Zosia?

Rozwiązanie:

Zrozumienie treści: Mamy dwie osoby: Jan i Zosia. Mamy dwie relacje wiekowe: obecny wiek i wiek sześć lat temu. Pytają nas o obecny wiek Jana i Zosi.
Wprowadzenie oznaczeń:
- x – obecny wiek Jana
- y – obecny wiek Zosi
Ułożenie równań:
- "Jan jest dwa razy starszy od Zosi" –> x = 2y
- "Sześć lat temu Jan był trzy razy starszy od Zosi" –> x - 6 = 3(y - 6)
Rozwiązanie równań: Podstawiamy pierwsze równanie do drugiego:
- 2y - 6 = 3(y - 6)
- 2y - 6 = 3y - 18
- -y = -12
- y = 12
Wracamy do pierwszego równania:
- x = 2 * 12
- x = 24
Sprawdzenie rozwiązania:
- Jan ma 24 lata, a Zosia ma 12 lat. Jan jest dwa razy starszy od Zosi (24 = 2 * 12) – zgadza się!
- Sześć lat temu Jan miał 18 lat (24 - 6 = 18), a Zosia miała 6 lat (12 - 6 = 6). Jan był trzy razy starszy od Zosi (18 = 3 * 6) – zgadza się!

Odpowiedź: Jan ma 24 lata, a Zosia ma 12 lat.

Wskazówki i Triki

Oto kilka dodatkowych wskazówek, które mogą Ci pomóc w rozwiązywaniu zadań z wiekiem:

Ćwicz, ćwicz i jeszcze raz ćwicz! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz schematy i triki.
Nie bój się prosić o pomoc. Jeśli masz problem z jakimś zadaniem, zapytaj nauczyciela, rodzica lub kolegę.
Szukaj wzorów. Wiele zadań z wiekiem ma podobną strukturę. Spróbuj zidentyfikować te wzory.
Bądź cierpliwy. Rozwiązywanie zadań z wiekiem może wymagać czasu i wysiłku. Nie zrażaj się, jeśli nie uda Ci się rozwiązać zadania za pierwszym razem.
Używaj kalkulatora do obliczeń. Skup się na logicznym rozumowaniu i układaniu równań, a kalkulator pomoże Ci uniknąć błędów rachunkowych.

Podsumowanie

Zadania z wiekiem w klasie 8 to doskonały sposób na rozwijanie umiejętności matematycznych i logicznych. Pamiętaj o kluczowych strategiach: zrozumienie treści, wprowadzenie oznaczeń, ułożenie równań, rozwiązanie równań i sprawdzenie rozwiązania. Ćwicz regularnie, nie bój się prosić o pomoc i bądź cierpliwy, a na pewno opanujesz sztukę rozwiązywania zadań z wiekiem. Pamiętajcie, każdy może to zrobić! To tylko kwestia praktyki i odpowiedniego podejścia.

Mamy nadzieję, że ten artykuł pomógł Wam zrozumieć, jak rozwiązywać zadania z wiekiem. Powodzenia na lekcjach matematyki!