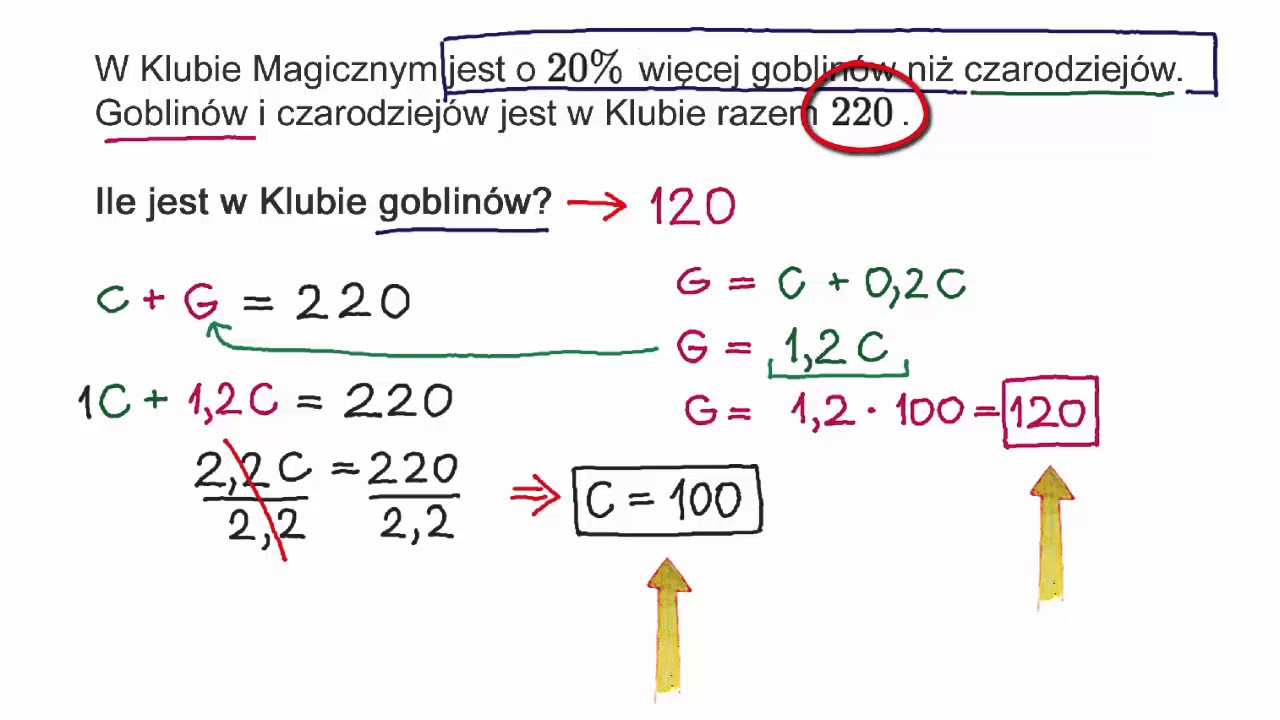
Zadania Z Procentami Klasa 7

W siódmej klasie szkoły podstawowej zadania z procentami stają się istotną częścią programu nauczania matematyki. Zrozumienie i opanowanie tych zadań jest kluczowe dla dalszej edukacji matematycznej oraz dla umiejętności radzenia sobie w życiu codziennym. Celem tego artykułu jest kompleksowe omówienie zadań z procentami, przedstawienie różnych typów zadań, metod ich rozwiązywania oraz pokazanie, jak wykorzystać tę wiedzę w praktyce.

Podstawy procentów

Zanim przejdziemy do rozwiązywania zadań, ważne jest, aby zrozumieć, czym właściwie jest procent. Procent to sposób wyrażenia liczby jako ułamka o mianowniku 100. Oznacza to, że 1% to 1/100, czyli 0,01. Znak procentu (%) oznacza "na sto".

Zamiana procentu na ułamek i odwrotnie: Aby zamienić procent na ułamek, dzielimy go przez 100. Na przykład, 25% to 25/100, co po skróceniu daje 1/4. Aby zamienić ułamek na procent, mnożymy go przez 100. Na przykład, 0,75 to 0,75 * 100 = 75%.

Obliczanie procentu danej liczby

Najprostszym typem zadań z procentami jest obliczanie procentu danej liczby. Aby to zrobić, zamieniamy procent na ułamek lub liczbę dziesiętną i mnożymy przez daną liczbę.

Przykład: Oblicz 20% z liczby 150.

Zamieniamy 20% na 0,20 (20/100 = 0,20). Następnie mnożymy 0,20 * 150 = 30. Zatem 20% z 150 to 30.

Można też użyć proporcji: 100% - 150; 20% - x. Stąd x = (20 * 150) / 100 = 30.

Typy zadań z procentami

Zadania z procentami mogą przyjmować różne formy. Oto kilka najczęstszych typów:

Obliczanie, jakim procentem jednej liczby jest druga liczba

W tego typu zadaniach musimy ustalić, jaki procent stanowi jedna liczba w stosunku do drugiej. Aby to zrobić, dzielimy jedną liczbę przez drugą i mnożymy przez 100.

Przykład: Jaki procent liczby 80 stanowi liczba 20?

Dzielimy 20 przez 80: 20 / 80 = 0,25. Następnie mnożymy przez 100: 0,25 * 100 = 25%. Zatem liczba 20 stanowi 25% liczby 80.

Można również ułożyć proporcję: 80 - 100%; 20 - x. Stąd x = (20 * 100) / 80 = 25%.

Obliczanie liczby, gdy dany jest jej procent

W tego typu zadaniach znamy procent liczby i musimy znaleźć tę liczbę. Aby to zrobić, dzielimy dany procent na ułamek lub liczbę dziesiętną, a następnie dzielimy daną wartość przez ten ułamek/liczbę dziesiętną.

Przykład: 25% pewnej liczby to 50. Jaka to liczba?

Zamieniamy 25% na 0,25 (25/100 = 0,25). Następnie dzielimy 50 przez 0,25: 50 / 0,25 = 200. Zatem szukana liczba to 200.

Alternatywnie: 25% - 50; 100% - x. Stąd x = (100 * 50) / 25 = 200.

Zadania z podwyżkami i obniżkami

Te zadania dotyczą zmian wartości o pewien procent. Aby obliczyć nową wartość, musimy najpierw obliczyć wartość zmiany (podwyżki lub obniżki), a następnie dodać ją do pierwotnej wartości (w przypadku podwyżki) lub odjąć ją od pierwotnej wartości (w przypadku obniżki).

Przykład: Cena towaru, który kosztował 120 zł, została podwyższona o 15%. Jaka jest nowa cena towaru?

Obliczamy podwyżkę: 15% z 120 zł to 0,15 * 120 = 18 zł. Następnie dodajemy podwyżkę do pierwotnej ceny: 120 zł + 18 zł = 138 zł. Zatem nowa cena towaru to 138 zł.

Można to również obliczyć jednym działaniem: 120 * 1,15 = 138 zł (gdzie 1,15 to 100% + 15%).

Przykład: Cena towaru, który kosztował 80 zł, została obniżona o 20%. Jaka jest nowa cena towaru?

Obliczamy obniżkę: 20% z 80 zł to 0,20 * 80 = 16 zł. Następnie odejmujemy obniżkę od pierwotnej ceny: 80 zł - 16 zł = 64 zł. Zatem nowa cena towaru to 64 zł.

Można to również obliczyć jednym działaniem: 80 * 0,80 = 64 zł (gdzie 0,80 to 100% - 20%).

Zadania z procentem składanym

Ten typ zadań występuje zazwyczaj w kontekście finansowym, np. przy obliczaniu odsetek od lokat bankowych. Procent składany oznacza, że odsetki naliczane są od kapitału początkowego powiększonego o dotychczas naliczone odsetki.

Przykład: Wpłacono do banku 1000 zł na lokatę roczną z oprocentowaniem 5% w skali roku. Jaki będzie stan konta po dwóch latach, jeśli odsetki są kapitalizowane rocznie?

Po pierwszym roku stan konta wyniesie: 1000 + (0,05 * 1000) = 1000 + 50 = 1050 zł.

Po drugim roku stan konta wyniesie: 1050 + (0,05 * 1050) = 1050 + 52,50 = 1102,50 zł.

Zatem po dwóch latach na koncie będzie 1102,50 zł.

Można użyć wzoru na procent składany: Kwota końcowa = Kapitał początkowy * (1 + stopa procentowa)^liczba lat. W tym przypadku: 1000 * (1 + 0,05)^2 = 1000 * 1,05^2 = 1000 * 1,1025 = 1102,50 zł.

Przykłady z życia codziennego

Zadania z procentami mają szerokie zastosowanie w życiu codziennym. Oto kilka przykładów:

• Rabat w sklepie: Obliczanie ceny po obniżce. Na przykład: Spodnie kosztują 150 zł, a rabat wynosi 20%. Ile zapłacę?
• Podatek VAT: Obliczanie ceny brutto (z VAT) towaru, znając cenę netto (bez VAT). Na przykład: Cena netto komputera to 2500 zł, a VAT wynosi 23%. Jaka jest cena brutto?
• Oprocentowanie kredytu: Obliczanie kosztu kredytu w skali roku. Na przykład: Kredyt w wysokości 5000 zł z oprocentowaniem 10% rocznie. Ile zapłacę odsetek po roku?
• Statystyki: Analiza danych statystycznych wyrażonych w procentach. Na przykład: W badaniu opinii publicznej 60% osób popiera dany projekt.
• Planowanie budżetu: Obliczanie procentowego udziału poszczególnych wydatków w budżecie domowym. Na przykład: Na jedzenie wydajemy 30% budżetu, na mieszkanie 40%, a na rozrywkę 10%.

Przykład z danymi: Według danych GUS (Głównego Urzędu Statystycznego) w 2023 roku inflacja w Polsce wyniosła średnio 11,4%. Oznacza to, że ceny towarów i usług wzrosły średnio o 11,4% w porównaniu z rokiem poprzednim. Jeśli produkt kosztował w 2022 roku 100 zł, to w 2023 roku kosztowałby średnio 111,40 zł (100 + 11,4% z 100).

Wskazówki dotyczące rozwiązywania zadań

Oto kilka wskazówek, które mogą pomóc w rozwiązywaniu zadań z procentami:

• Przeczytaj uważnie treść zadania: Upewnij się, że rozumiesz, o co pytają w zadaniu. Zidentyfikuj dane i szukane wartości.
• Zapisz dane i szukane: Zapisanie danych i szukanych w uporządkowany sposób pomoże Ci lepiej zrozumieć problem.
• Zamień procenty na ułamki lub liczby dziesiętne: To ułatwi obliczenia.
• Użyj proporcji: Ułożenie proporcji może ułatwić rozwiązanie niektórych typów zadań.
• Sprawdź odpowiedź: Po rozwiązaniu zadania sprawdź, czy Twoja odpowiedź ma sens w kontekście zadania.
• Ćwicz regularnie: Im więcej zadań rozwiążesz, tym lepiej opanujesz umiejętność rozwiązywania zadań z procentami.

Podsumowanie

Zadania z procentami są ważnym elementem programu nauczania matematyki w siódmej klasie. Opanowanie tych zadań jest kluczowe dla dalszej edukacji i dla umiejętności radzenia sobie w życiu codziennym. Poprzez zrozumienie podstawowych pojęć, poznanie różnych typów zadań i regularne ćwiczenia, każdy uczeń może osiągnąć sukces w rozwiązywaniu zadań z procentami.

Zachęcamy do dalszego ćwiczenia i poszukiwania przykładów zastosowania procentów w życiu codziennym. Spróbuj rozwiązywać zadania z podręcznika, arkuszy ćwiczeń, a także te, które znajdziesz w internecie. Powodzenia!