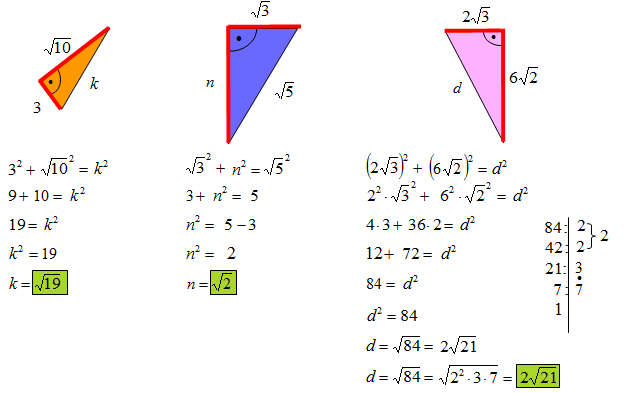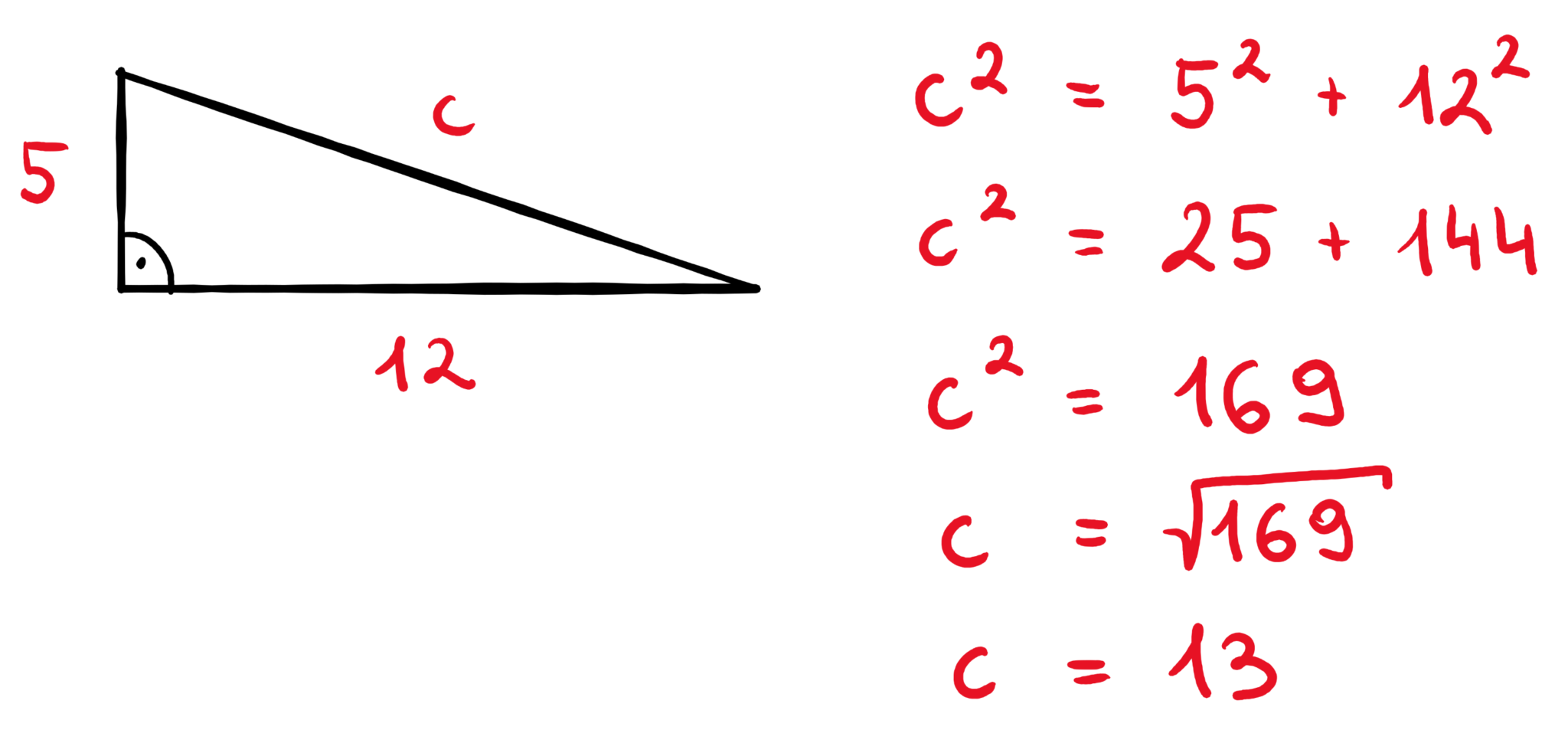Zadania Z Pitagorasa Klasa 8

Witaj w świecie zadań z twierdzenia Pitagorasa! Rozumiem, że jesteś w 8 klasie i być może właśnie zmagasz się z tym tematem. Nie martw się, wiele osób ma trudności na początku. Chodzi o zrozumienie związku między bokami trójkąta prostokątnego i umiejętność wykorzystania tego związku do rozwiązywania zadań. Pokażę Ci, jak to zrobić krok po kroku.

Co to jest twierdzenie Pitagorasa?

Najpierw przypomnijmy sobie, o co w ogóle chodzi. Twierdzenie Pitagorasa dotyczy trójkątów prostokątnych, czyli takich, które mają jeden kąt prosty (90 stopni). Najdłuższy bok trójkąta prostokątnego, leżący naprzeciwko kąta prostego, nazywamy przeciwprostokątną (oznaczamy go literą c). Pozostałe dwa boki to przyprostokątne (oznaczamy je literami a i b).

Twierdzenie Pitagorasa mówi, że suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Matematycznie zapisujemy to tak:

a² + b² = c²

Proste, prawda? Ale jak to się przekłada na rozwiązywanie zadań?

Dlaczego warto znać twierdzenie Pitagorasa?

Może wydawać się, że to tylko kolejny wzór do zapamiętania. Ale prawda jest taka, że twierdzenie Pitagorasa ma ogromne zastosowanie w życiu codziennym i w wielu dziedzinach, takich jak:

Budownictwo: Obliczanie długości przekątnych w prostokątnych budynkach, sprawdzanie, czy ściany są ustawione pod kątem prostym.
Nawigacja: Określanie odległości między punktami na mapie.
Inżynieria: Projektowanie mostów, budynków i innych konstrukcji.
Grafika komputerowa: Obliczanie odległości między pikselami.
I... rozwiązywanie zadań na matematyce w 8 klasie! 😉

Typowe zadania z twierdzenia Pitagorasa

Zadania na twierdzenie Pitagorasa zwykle sprowadzają się do jednej z tych sytuacji:

Znane są długości przyprostokątnych (a i b), a trzeba obliczyć długość przeciwprostokątnej (c).
Znana jest długość przeciwprostokątnej (c) i jednej z przyprostokątnych (np. a), a trzeba obliczyć długość drugiej przyprostokątnej (b).
Zadanie "ukryte", gdzie trzeba najpierw znaleźć trójkąt prostokątny, żeby móc użyć twierdzenia.

Przykład 1: Obliczanie przeciwprostokątnej

Zadanie: Przyprostokątne trójkąta prostokątnego mają długości 3 cm i 4 cm. Oblicz długość przeciwprostokątnej.

Rozwiązanie:

Zapisujemy dane: a = 3 cm, b = 4 cm, c = ?
Stosujemy twierdzenie Pitagorasa: a² + b² = c²
Podstawiamy dane: 3² + 4² = c²
Obliczamy: 9 + 16 = c² => 25 = c²
Wyciągamy pierwiastek kwadratowy: c = √25 => c = 5 cm

Odpowiedź: Długość przeciwprostokątnej wynosi 5 cm.

Przykład 2: Obliczanie przyprostokątnej

Zadanie: Przeciwprostokątna trójkąta prostokątnego ma długość 13 cm, a jedna z przyprostokątnych ma długość 5 cm. Oblicz długość drugiej przyprostokątnej.

Rozwiązanie:

Zapisujemy dane: c = 13 cm, a = 5 cm, b = ?
Stosujemy twierdzenie Pitagorasa: a² + b² = c²
Podstawiamy dane: 5² + b² = 13²
Obliczamy: 25 + b² = 169 => b² = 169 - 25 => b² = 144
Wyciągamy pierwiastek kwadratowy: b = √144 => b = 12 cm

Odpowiedź: Długość drugiej przyprostokątnej wynosi 12 cm.

Przykład 3: Zadanie z "ukrytym" trójkątem

Zadanie: Drabina o długości 5 metrów jest oparta o ścianę. Jej dolny koniec znajduje się w odległości 3 metrów od ściany. Na jakiej wysokości sięga drabina?

Rozwiązanie:

Zauważ, że drabina, ściana i odległość od ściany tworzą trójkąt prostokątny. Drabina to przeciwprostokątna, odległość od ściany to jedna przyprostokątna, a wysokość, na jaką sięga drabina, to druga przyprostokątna.

Zapisujemy dane: c = 5 m, a = 3 m, b = ?
Stosujemy twierdzenie Pitagorasa: a² + b² = c²
Podstawiamy dane: 3² + b² = 5²
Obliczamy: 9 + b² = 25 => b² = 25 - 9 => b² = 16
Wyciągamy pierwiastek kwadratowy: b = √16 => b = 4 m

Odpowiedź: Drabina sięga na wysokość 4 metrów.

Typowe błędy i jak ich unikać

Podczas rozwiązywania zadań z twierdzenia Pitagorasa często popełniane są pewne błędy. Oto kilka z nich i sposoby, jak ich unikać:

Pomylenie przyprostokątnej z przeciwprostokątną: Zawsze upewnij się, który bok jest najdłuższy i leży naprzeciwko kąta prostego. To jest przeciwprostokątna.
Złe podstawienie do wzoru: Upewnij się, że podstawiasz wartości do odpowiednich liter we wzorze a² + b² = c².
Zapominanie o wyciągnięciu pierwiastka kwadratowego: Po obliczeniu c² (lub a², b²) pamiętaj o wyciągnięciu pierwiastka, aby otrzymać długość boku (c, a, b).
Brak jednostek: Pamiętaj o podawaniu jednostek (cm, m, km itp.) w odpowiedzi.
Zaokrąglanie wyników zbyt wcześnie: Jeśli wynik pierwiastka kwadratowego jest liczbą niewymierną (np. √2), zaokrąglaj go dopiero w końcowym wyniku, aby uniknąć błędów.

Jak skutecznie uczyć się twierdzenia Pitagorasa?

Oto kilka wskazówek, które pomogą Ci opanować twierdzenie Pitagorasa:

Zrozumienie, a nie tylko zapamiętywanie: Skup się na zrozumieniu, dlaczego twierdzenie Pitagorasa działa, a nie tylko na zapamiętaniu wzoru. Możesz znaleźć wizualne dowody twierdzenia w internecie.
Rozwiązywanie wielu zadań: Ćwiczenie czyni mistrza! Rozwiązuj jak najwięcej różnych zadań, aby utrwalić wiedzę i nauczyć się rozpoznawać różne typy zadań.
Praca z rysunkami: Zawsze rysuj trójkąt prostokątny i oznaczaj na nim boki. To pomoże Ci lepiej zrozumieć zadanie i uniknąć pomyłek.
Praca w grupie: Dyskutuj o zadaniach z kolegami i koleżankami z klasy. Wytłumaczenie komuś, jak rozwiązać zadanie, jest doskonałym sposobem na utrwalenie wiedzy.
Korzystanie z zasobów online: W internecie znajdziesz wiele darmowych materiałów do nauki twierdzenia Pitagorasa, takich jak:
- Filmy instruktażowe na YouTube
- Interaktywne ćwiczenia na stronach edukacyjnych
- Generator zadań online
Nie bój się pytać: Jeśli masz jakieś wątpliwości, nie bój się pytać nauczyciela lub kogoś, kto dobrze rozumie ten temat.

Adresowanie kontrargumentów

Czasami uczniowie pytają: "Po co nam to twierdzenie Pitagorasa? Kiedy to się przyda w życiu?". To ważny argument! Jak już wspominałem, ma zastosowanie w wielu dziedzinach. Co więcej, uczy logicznego myślenia i rozwiązywania problemów, co przydaje się w każdej dziedzinie życia, niezależnie od tego, co będziesz robić w przyszłości.

Inny kontrargument to: "Wzór jest trudny do zapamiętania". To prawda, ale z czasem i ćwiczeniami zapamiętasz go automatycznie. Skup się na zrozumieniu, a zapamiętanie przyjdzie samo. Wyobraź sobie, że budujesz dom z klocków. Potrzebujesz odpowiednich klocków, żeby dom był stabilny. Twierdzenie Pitagorasa to taki "klocek" w świecie matematyki, który pozwala budować bardziej skomplikowane konstrukcje.

Podsumowanie i kolejne kroki

Twierdzenie Pitagorasa to fundamentalne narzędzie w matematyce, które ma szerokie zastosowanie w życiu codziennym. Nie zrażaj się trudnościami, tylko ćwicz regularnie, a z pewnością opanujesz ten temat. Pamiętaj o rysowaniu trójkątów, oznaczaniu boków i sprawdzaniu, czy dobrze podstawiasz wartości do wzoru.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć twierdzenie Pitagorasa i jak rozwiązywać zadania z nim związane. Pamiętaj, że najważniejsza jest praktyka! Im więcej zadań rozwiążesz, tym pewniej będziesz się czuć z tym tematem.

Spróbuj teraz rozwiązać kilka zadań z podręcznika lub z internetu. Jakie masz teraz przemyślenia? Czy czujesz się pewniej w rozwiązywaniu zadań z twierdzenia Pitagorasa?