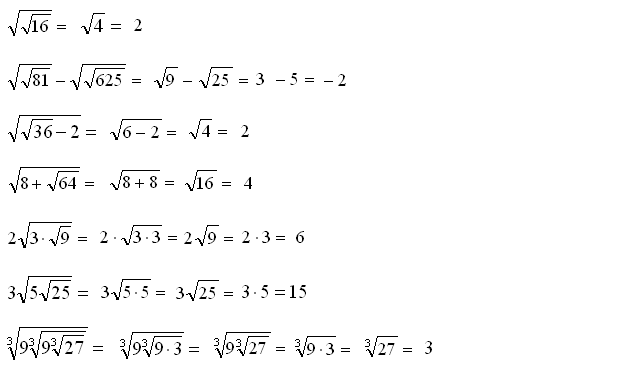Zadania Z Pierwiastkami Klasa 8

Czy zadania z pierwiastkami w klasie 8 spędzają Ci sen z powiek? Wiem, że dla wielu uczniów temat pierwiastków bywa trudny i niezrozumiały. Nie jesteś sam! Wielu z nas na początku zmaga się z tą tematyką. Najważniejsze to zrozumieć, że opanowanie pierwiastków jest kluczowe do dalszej nauki matematyki, a także przydatne w wielu sytuacjach życiowych.

W tym artykule postaram się rozwiać Twoje wątpliwości i pokazać, że zadania z pierwiastkami wcale nie muszą być takie straszne. Podejdziemy do tematu krok po kroku, wyjaśniając najważniejsze pojęcia i prezentując praktyczne przykłady.

Co to właściwie jest pierwiastek?

Zanim przejdziemy do rozwiązywania zadań, musimy zrozumieć, czym tak naprawdę jest pierwiastek. Wyobraź sobie, że masz kwadrat o polu 9. Jaką długość ma bok tego kwadratu? Oczywiście 3, ponieważ 3 * 3 = 9. I właśnie to jest pierwiastek kwadratowy z 9!

Formalnie: Pierwiastek kwadratowy z liczby a to taka liczba b, która podniesiona do kwadratu daje liczbę a. Zapisujemy to tak: √a = b, jeśli b² = a.

Podobnie, pierwiastek sześcienny z liczby a to taka liczba b, która podniesiona do sześcianu daje liczbę a. Zapisujemy to tak: ∛a = b, jeśli b³ = a.

Przykłady:

• √4 = 2, bo 2² = 4
• √25 = 5, bo 5² = 25
• ∛8 = 2, bo 2³ = 8
• ∛27 = 3, bo 3³ = 27

Dlaczego pierwiastki są ważne? Real-world impact

Możesz się zastanawiać, po co w ogóle uczyć się o pierwiastkach. Otóż, pierwiastki mają szerokie zastosowanie w życiu codziennym i w różnych dziedzinach nauki.

• Architektura i budownictwo: Obliczanie długości przekątnych, powierzchni, objętości.
• Fizyka: Obliczanie prędkości, przyspieszenia, energii.
• Informatyka: Algorytmy, grafika komputerowa.
• Finanse: Obliczanie oprocentowania składanego.
• Nawet w kuchni!: Przy planowaniu posiłków, gdy musisz zwiększyć lub zmniejszyć proporcje składników zachowując pewne relacje.

Zrozumienie pierwiastków pozwala na rozwiązywanie problemów, które pojawiają się w tych dziedzinach. Wyobraź sobie architekta projektującego budynek. Musi on precyzyjnie obliczyć długość belki wspierającej konstrukcję. Do tego niezbędna jest wiedza o pierwiastkach!

Typowe zadania z pierwiastkami w klasie 8

W klasie 8 najczęściej spotykamy się z następującymi typami zadań z pierwiastkami:

• Obliczanie wartości pierwiastków: Znajdowanie wartości pierwiastka kwadratowego lub sześciennego z danej liczby.
• Upraszczanie wyrażeń z pierwiastkami: Wykorzystywanie własności pierwiastków do upraszczania wyrażeń algebraicznych.
• Usuwanie niewymierności z mianownika: Pozbywanie się pierwiastka z mianownika ułamka.
• Porównywanie liczb z pierwiastkami: Ustalanie, która z dwóch liczb z pierwiastkami jest większa.
• Rozwiązywanie równań z pierwiastkami: Znajdowanie wartości zmiennej spełniającej równanie, w którym występuje pierwiastek.

Przykłady i rozwiązania

Przyjrzyjmy się teraz kilku przykładom zadań i sposobom ich rozwiązywania.

Przykład 1: Oblicz wartość √64 + ∛-8

Rozwiązanie:

√64 = 8, bo 8² = 64

∛-8 = -2, bo (-2)³ = -8

Zatem √64 + ∛-8 = 8 + (-2) = 6

Przykład 2: Uprość wyrażenie √12 + √27

Rozwiązanie:

√12 = √(4 * 3) = √4 * √3 = 2√3

√27 = √(9 * 3) = √9 * √3 = 3√3

Zatem √12 + √27 = 2√3 + 3√3 = 5√3

Przykład 3: Usuń niewymierność z mianownika ułamka 2/√3

Rozwiązanie:

Aby usunąć niewymierność, mnożymy licznik i mianownik przez √3:

(2/√3) * (√3/√3) = (2√3) / 3

Przykład 4: Porównaj liczby √17 i 4

Rozwiązanie:

Podnosimy obie liczby do kwadratu:

(√17)² = 17

4² = 16

Ponieważ 17 > 16, to √17 > 4

Własności pierwiastków – Klucz do sukcesu

Znajomość własności pierwiastków jest niezbędna do rozwiązywania zadań. Oto najważniejsze z nich:

• √(a * b) = √a * √b (Pierwiastek z iloczynu jest równy iloczynowi pierwiastków)
• √(a / b) = √a / √b (Pierwiastek z ilorazu jest równy ilorazowi pierwiastków)
• (√a)² = a (Pierwiastek kwadratowy podniesiony do kwadratu daje liczbę pod pierwiastkiem)
• ∛(a * b) = ∛a * ∛b (Pierwiastek sześcienny z iloczynu jest równy iloczynowi pierwiastków sześciennych)
• ∛(a / b) = ∛a / ∛b (Pierwiastek sześcienny z ilorazu jest równy ilorazowi pierwiastków sześciennych)
• (∛a)³ = a (Pierwiastek sześcienny podniesiony do sześcianu daje liczbę pod pierwiastkiem)

Zapamiętaj te wzory! Pomogą Ci one w upraszczaniu wyrażeń i rozwiązywaniu zadań.

Częste błędy i jak ich unikać

Podczas rozwiązywania zadań z pierwiastkami łatwo o pomyłkę. Oto kilka najczęstszych błędów i sposoby, jak ich unikać:

• Błędne obliczanie pierwiastków: Zawsze sprawdź, czy liczba pod pierwiastkiem jest kwadratem lub sześcianem jakiejś liczby. Użyj kalkulatora, jeśli masz wątpliwości.
• Zapominanie o własnościach pierwiastków: Przed przystąpieniem do rozwiązywania zadania przypomnij sobie wszystkie własności pierwiastków.
• Błędne upraszczanie wyrażeń: Upewnij się, że poprawnie wyłączasz czynniki przed znak pierwiastka.
• Zapominanie o kolejności działań: Pamiętaj, że pierwiastkowanie ma wyższy priorytet niż dodawanie i odejmowanie.
• Błędy w usuwaniu niewymierności: Upewnij się, że mnożysz licznik i mianownik przez odpowiedni czynnik.

Przeciwności - Argumenty "przeciw" i dlaczego są niesłuszne

Niektórzy mogą twierdzić, że nauka pierwiastków jest bezużyteczna, ponieważ w dzisiejszych czasach wszystko można obliczyć za pomocą kalkulatora. To częściowo prawda, ale zrozumienie koncepcji pierwiastków pozwala na:

• Logiczne myślenie: Rozwiązywanie zadań z pierwiastkami rozwija umiejętność logicznego myślenia i rozwiązywania problemów.
• Rozumienie bardziej zaawansowanej matematyki: Wiedza o pierwiastkach jest niezbędna do zrozumienia bardziej zaawansowanych tematów, takich jak funkcje, geometria analityczna czy rachunek różniczkowy i całkowy.
• Krytyczne myślenie: Kalkulator daje wynik, ale nie mówi Ci dlaczego. Zrozumienie pierwiastków pozwala na krytyczną ocenę wyników i unikanie błędów.

Inni mogą uważać, że nauka na pamięć wzorów jest niepotrzebna. Owszem, ważniejsze jest zrozumienie, ale znajomość podstawowych wzorów przyspiesza rozwiązywanie zadań i ułatwia pracę.

Rozwiązanie trudności – Klucz do sukcesu

Jak więc pokonać trudności związane z zadaniami z pierwiastkami? Oto kilka sprawdzonych metod:

• Ćwicz regularnie: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz temat.
• Korzystaj z różnych źródeł: Sięgnij po podręczniki, zbiory zadań, internetowe kursy i filmy instruktażowe.
• Szukaj pomocy: Nie wstydź się pytać nauczyciela, kolegów lub korepetytora, jeśli masz problemy.
• Pracuj w grupie: Wspólne rozwiązywanie zadań może być bardzo pomocne.
• Zrób sobie przerwę: Jeśli czujesz się zmęczony, odpocznij i wróć do zadania później.

Pamiętaj, że każdy może nauczyć się matematyki. Wystarczy trochę wysiłku i cierpliwości!

Podsumowanie

Zadania z pierwiastkami w klasie 8 nie muszą być straszne. Wystarczy zrozumieć podstawowe pojęcia, poznać własności pierwiastków, unikać częstych błędów i ćwiczyć regularnie. Pamiętaj, że wiedza o pierwiastkach jest przydatna w życiu codziennym i niezbędna do dalszej nauki matematyki.

W tym artykule omówiliśmy:

• Definicję pierwiastka kwadratowego i sześciennego
• Przykłady zastosowań pierwiastków w życiu codziennym
• Typowe zadania z pierwiastkami w klasie 8
• Własności pierwiastków
• Częste błędy i jak ich unikać
• Argumenty "przeciw" i dlaczego są niesłuszne
• Sposoby pokonywania trudności

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć temat pierwiastków. Teraz czas na praktykę! Sięgnij po zbiór zadań i spróbuj rozwiązać kilka przykładów. Powodzenia!

Jakie zadanie z pierwiastkami sprawia Ci największą trudność i jak spróbujesz się z nim zmierzyć?