Z Graniastosłupa Którego Wszystkie Krawędzie Mają Długość 10 Cm

Graniastosłup, którego wszystkie krawędzie mają długość 10 cm, to fascynujący obiekt geometryczny, który łączy w sobie regularność i symetrię. Jego analiza pozwala na dogłębne zrozumienie własności graniastosłupów, w tym pól powierzchni, objętości, a także związków pomiędzy jego elementami składowymi.

Zaczniemy od rozważenia różnych typów graniastosłupów, które mogą spełniać warunek, że wszystkie krawędzie mają długość 10 cm. Graniastosłup to bryła, której podstawy są przystającymi wielokątami, a ściany boczne są równoległobokami. Najprostszym przypadkiem jest graniastosłup trójkątny. Jeśli jego podstawą jest trójkąt równoboczny o boku 10 cm, a wysokość graniastosłupa również wynosi 10 cm, to mamy do czynienia z graniastosłupem, który spełnia nasze kryteria.

Następnie przyjrzyjmy się graniastosłupowi czworokątnemu. Najbardziej oczywistym przykładem jest sześcian, w którym wszystkie krawędzie mają długość 10 cm. Jest to szczególny przypadek graniastosłupa prostego, gdzie podstawą jest kwadrat. Ale co z innymi graniastosłupami czworokątnymi? Czy istnieją inne, które mogą spełniać warunek równych krawędzi? Otóż tak, możemy sobie wyobrazić graniastosłup, którego podstawą jest romb o boku 10 cm, a wysokość również wynosi 10 cm. W takim przypadku wszystkie krawędzie również będą miały długość 10 cm. Kąty w rombie nie muszą być proste, co odróżnia go od sześcianu.

Co z graniastosłupami o większej liczbie boków w podstawie? Graniastosłup pięciokątny, sześciokątny, i tak dalej. W zasadzie, dla każdego n-kąta foremnego o boku 10 cm, możemy zbudować graniastosłup prosty o wysokości 10 cm, który będzie spełniał nasz warunek. Ważne jest, aby podstawa była wielokątem foremnym, ponieważ wtedy wszystkie krawędzie boczne będą miały tę samą długość, czyli 10 cm.

Obliczenia związane z takim graniastosłupem wymagają znajomości geometrii płaskiej i przestrzennej. Dla graniastosłupa trójkątnego, którego podstawą jest trójkąt równoboczny, pole podstawy wynosi (a^2 * sqrt(3)) / 4, gdzie a = 10 cm. Zatem pole podstawy to (100 * sqrt(3)) / 4 = 25 * sqrt(3) cm^2. Pole powierzchni bocznej takiego graniastosłupa to 3 * a * h, gdzie a = 10 cm i h = 10 cm. Zatem pole powierzchni bocznej to 3 * 10 * 10 = 300 cm^2. Pole powierzchni całkowitej to suma pól dwóch podstaw i pola powierzchni bocznej, czyli 2 * 25 * sqrt(3) + 300 = 50 * sqrt(3) + 300 cm^2. Objętość takiego graniastosłupa to pole podstawy pomnożone przez wysokość, czyli 25 * sqrt(3) * 10 = 250 * sqrt(3) cm^3.

W przypadku sześcianu, obliczenia są jeszcze prostsze. Pole powierzchni jednej ściany to a^2 = 10 * 10 = 100 cm^2. Sześcian ma 6 ścian, więc pole powierzchni całkowitej to 6 * 100 = 600 cm^2. Objętość sześcianu to a^3 = 10 * 10 * 10 = 1000 cm^3.

Analiza Pola Powierzchni i Objętości

Porównując graniastosłup trójkątny i sześcian o krawędzi 10 cm, zauważamy znaczące różnice w polu powierzchni i objętości. Sześcian ma większą objętość (1000 cm^3) niż graniastosłup trójkątny (250 * sqrt(3) cm^3 ≈ 433 cm^3). Podobnie, pole powierzchni sześcianu (600 cm^2) jest większe niż pole powierzchni całkowitej graniastosłupa trójkątnego (50 * sqrt(3) + 300 cm^2 ≈ 386.6 cm^2).

Zastanówmy się, jak zmienia się pole powierzchni i objętość w zależności od liczby boków w podstawie graniastosłupa. Im więcej boków ma wielokąt foremny w podstawie, tym bardziej graniastosłup zbliża się do walca. Przy bardzo dużej liczbie boków, graniastosłup w granicy staje się walcem o promieniu, który zależy od długości boku wielokąta foremnego, i wysokości równej 10 cm.

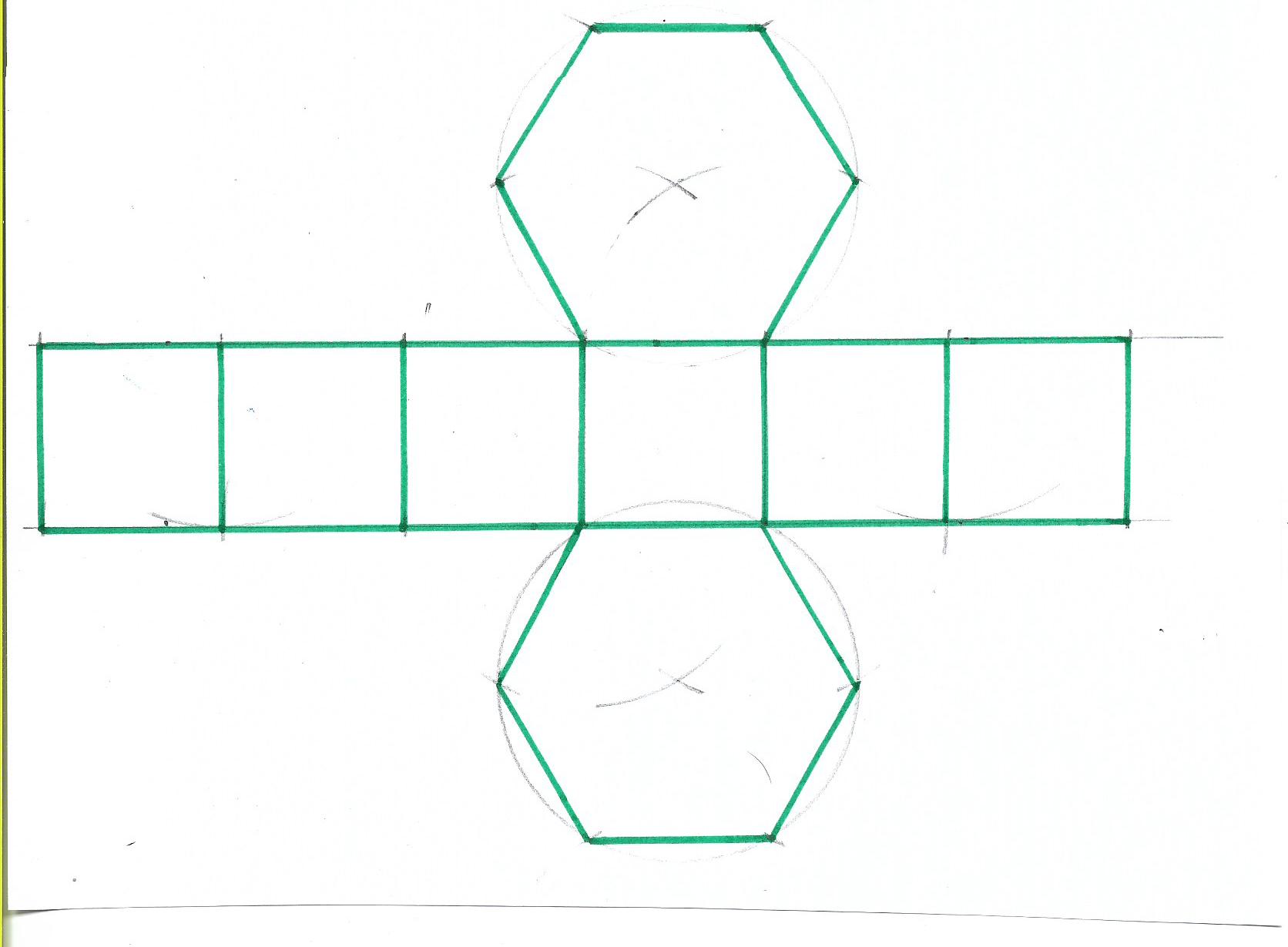
Dla graniastosłupa sześciokątnego foremnego o boku 10 cm i wysokości 10 cm, pole podstawy wynosi (3 * sqrt(3) * a^2) / 2 = (3 * sqrt(3) * 100) / 2 = 150 * sqrt(3) cm^2. Pole powierzchni bocznej pozostaje takie samo jak dla graniastosłupa trójkątnego, czyli 6 * a * h = 6 * 10 * 10 = 600 cm^2. Pole powierzchni całkowitej to 2 * 150 * sqrt(3) + 600 = 300 * sqrt(3) + 600 cm^2 ≈ 1119.6 cm^2. Objętość takiego graniastosłupa to pole podstawy pomnożone przez wysokość, czyli 150 * sqrt(3) * 10 = 1500 * sqrt(3) cm^3 ≈ 2598 cm^3.

Zauważamy, że w miarę wzrostu liczby boków w podstawie, objętość graniastosłupa rośnie. Pole powierzchni również rośnie, ale niekoniecznie monotonicznie w każdym przypadku.

Wróćmy do przypadku graniastosłupa czworokątnego, którego podstawą jest romb. Jeśli romb nie jest kwadratem, to jego kąty nie są proste. Niech kąt ostry w rombie wynosi α. Pole rombu wynosi a^2 * sin(α), gdzie a = 10 cm. Pole powierzchni bocznej graniastosłupa to 4 * a * h = 4 * 10 * 10 = 400 cm^2. Pole powierzchni całkowitej to 2 * a^2 * sin(α) + 400 = 2 * 100 * sin(α) + 400 = 200 * sin(α) + 400 cm^2. Objętość takiego graniastosłupa to pole podstawy pomnożone przez wysokość, czyli a^2 * sin(α) * h = 100 * sin(α) * 10 = 1000 * sin(α) cm^3. Widać, że pole powierzchni i objętość zależą od kąta α. Jeśli α = 90 stopni, to romb staje się kwadratem, a graniastosłup staje się sześcianem.

Podsumowanie i Dalsze Rozważania

Graniastosłup, którego wszystkie krawędzie mają długość 10 cm, to klasa obiektów geometrycznych, które różnią się kształtem podstawy. Analiza pola powierzchni i objętości różnych typów graniastosłupów pozwala na zrozumienie wpływu kształtu podstawy na własności całej bryły. Sześcian jest szczególnym przypadkiem takiego graniastosłupa, charakteryzującym się największą symetrią. Możemy rozważać inne aspekty, takie jak kąty nachylenia ścian bocznych, symetrie, a także możliwości konstrukcji takich graniastosłupów w przestrzeni trójwymiarowej. Interesujące byłoby również zbadanie, jak zmieniają się te własności, gdy długość krawędzi jest inna niż 10 cm, lub gdy krawędzie nie są równe. Możemy również zastanowić się nad możliwością "rozłożenia" takiego graniastosłupa na siatkę, czyli płaski wzór, który po złożeniu tworzy bryłę.