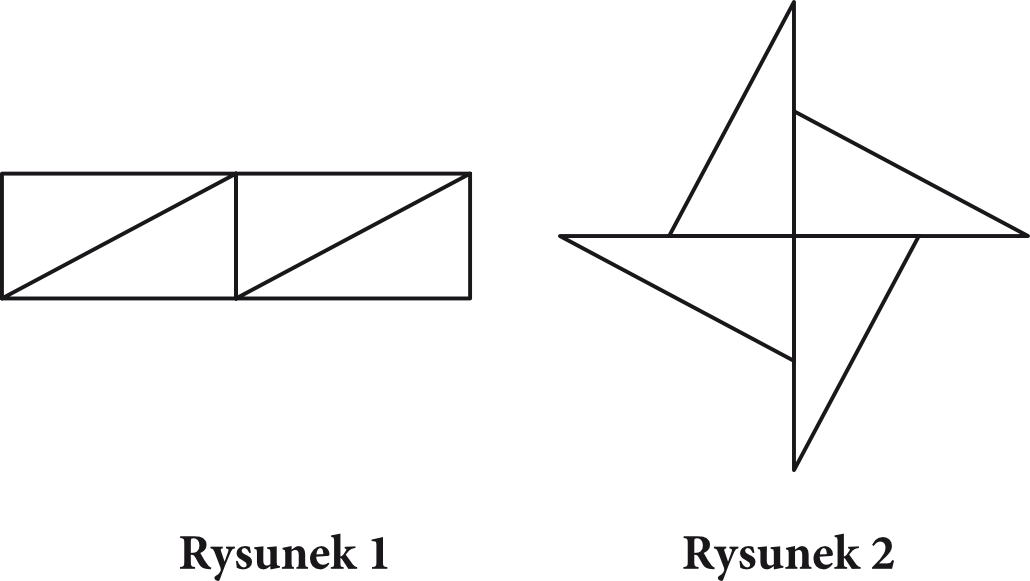
Z Czterech Jednakowych Równoległoboków Ułożono Figurę Przedstawioną Na Rysunku

Drodzy uczniowie,

Widzę, że macie pytania dotyczące figury utworzonej z czterech jednakowych równoległoboków. Przygotowałem dla Was szczegółowe omówienie tego zagadnienia, obejmujące analizę geometrii, właściwości i potencjalnych obliczeń związanych z taką konfiguracją.

Rozważmy cztery identyczne równoległoboki ułożone w taki sposób, że tworzą nową figurę. Istnieje wiele sposobów, w jakie mogą być one połączone, a konkretna konfiguracja ma zasadniczy wpływ na właściwości wynikowej figury.

Kluczowe parametry opisujące pojedynczy równoległobok to:

• Długość boku a
• Długość boku b
• Kąt ostry α (a tym samym kąt rozwarty 180° - α)
• Wysokość h_a opuszczona na bok a
• Wysokość h_b opuszczona na bok b

Pole pojedynczego równoległoboku P można obliczyć na kilka sposobów:

• P = a * h_a
• P = b * h_b
• P = a * b * sin(α)

Układając cztery identyczne równoległoboki, możemy uzyskać różne efekty w zależności od tego, jak je ze sobą połączymy. Przykładowe konfiguracje obejmują:

1. Ułożenie szeregowe: Równoległoboki są do siebie przyległe wzdłuż dłuższego boku (b), tworząc dłuższy równoległobok o tym samym kącie ostrym α. W takim przypadku długość dłuższego boku nowej figury wynosi 4b, a krótszy bok pozostaje bez zmian, czyli a. Pole figury jest równe 4P.
2. Ułożenie równoległe: Równoległoboki są do siebie przyległe wzdłuż krótszego boku (a), tworząc równoległobok o dłuższym boku b i krótszym boku 4a. Pole figury wynosi ponownie 4P.
3. Ułożenie w formie "rozety": Równoległoboki są połączone w taki sposób, że w centrum figury powstaje pusty obszar. Najczęściej dotyczy to sytuacji, gdy krótkie boki równoległoboków stykają się w jednym punkcie, tworząc kąt. Geometria tej figury jest bardziej skomplikowana i wymaga analizy kątów i długości boków, aby określić wymiary i pole pustego obszaru w środku. Pole całej figury nadal wynosi 4P, ale kształt i rozmiar pustego obszaru zależą od wartości kąta α.
4. Ułożenie w prostokąt (specjalny przypadek): Jeśli równoległoboki są prostokątami (czyli α = 90°), możemy ułożyć je tak, aby utworzyły większy prostokąt. Możemy ułożyć je 2x2 lub 1x4. W każdym przypadku pole będzie wynosić 4P, gdzie P jest polem pojedynczego prostokąta.
5. Ułożenie tworzące równoległobok o innej proporcji: Równoległoboki mogą być ułożone tak, że ich boki nie pokrywają się idealnie, ale tworzą nowy równoległobok o zmienionych proporcjach. Analiza takiej konfiguracji wymaga rozważenia wektorów reprezentujących boki równoległoboków i ich sumowania, aby określić wektory definiujące nowy równoległobok.

Analiza Kątów i Symetrii

Ważnym aspektem jest analiza kątów w miejscu połączenia równoległoboków. Kąty w równoległoboku spełniają relację: α + (180° - α) = 180°. Przy łączeniu równoległoboków należy uwzględnić, czy kąty przylegające do danego wierzchołka sumują się do 360°, co jest warunkiem koniecznym dla zamknięcia figury.

Symetria figury zależy od sposobu ułożenia równoległoboków. Ułożenia szeregowe i równoległe wykazują symetrię osiową. Ułożenie w formie "rozety" może mieć symetrię obrotową, jeśli równoległoboki są rozmieszczone równomiernie wokół centralnego punktu. Ułożenie losowe zazwyczaj nie ma żadnej symetrii.

Obliczenia i Przykłady

Załóżmy, że mamy równoległobok o bokach a = 5 cm, b = 8 cm i kącie ostrym α = 60°. Wtedy pole pojedynczego równoległoboku wynosi:

P = a * b * sin(α) = 5 cm * 8 cm * sin(60°) = 40 cm² * (√3/2) = 20√3 cm² ≈ 34.64 cm²

Rozważmy ułożenie szeregowe tych równoległoboków. Nowy równoległobok ma boki a = 5 cm i b' = 4 * 8 cm = 32 cm. Pole nowej figury to:

P' = 4 * P = 4 * 20√3 cm² = 80√3 cm² ≈ 138.56 cm²

W przypadku ułożenia w formie "rozety", gdzie krótkie boki równoległoboków stykają się w jednym punkcie, a kąt między sąsiednimi równoległobokami wynosi β, analiza geometrii staje się bardziej złożona. Wymaga ona rozważenia trójkątów tworzonych przez boki równoległoboków i obliczenia pola pustego obszaru na podstawie trygonometrii.

Podsumowując, ułożenie czterech identycznych równoległoboków może prowadzić do różnych figur o różnych właściwościach geometrycznych. Analiza kątów, symetrii i długości boków jest kluczowa do zrozumienia i obliczenia parametrów tych figur. Konkretny kształt i właściwości wynikowej figury zależą w dużym stopniu od sposobu połączenia równoległoboków. Mam nadzieję, że to szczegółowe wyjaśnienie pomoże Wam w zrozumieniu tego zagadnienia. Jeżeli macie dodatkowe pytania, śmiało pytajcie.