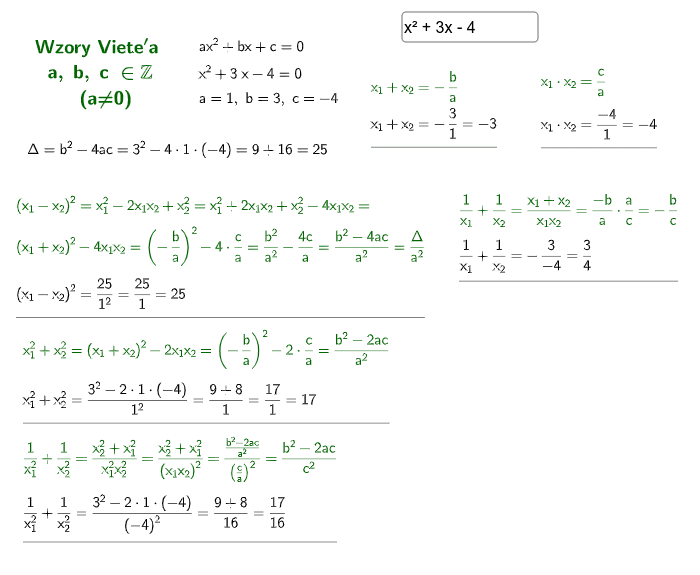Wzory Viete A Dla Wielomianu 3 Stopnia

Czy kiedykolwiek patrzyłeś na równanie wielomianowe i czułeś się zagubiony w gąszczu liczb i symboli? A może zastanawiałeś się, czy istnieje sposób na szybsze zrozumienie relacji między pierwiastkami a współczynnikami? Jeśli tak, to ten artykuł jest dla Ciebie. Zajmiemy się tutaj wzorami Viète'a dla wielomianu stopnia trzeciego – potężnym narzędziem, które, choć na pierwszy rzut oka może wydawać się skomplikowane, w rzeczywistości pozwala znacząco uprościć rozwiązywanie niektórych problemów.

Zrozumienie wzorów Viète'a otwiera nowe perspektywy w analizie równań wielomianowych. Pozwala nie tylko na efektywne rozwiązywanie zadań, ale także na głębsze zrozumienie matematycznych zależności. Niezależnie od tego, czy jesteś uczniem przygotowującym się do matury, studentem, czy po prostu entuzjastą matematyki, znajomość tych wzorów z pewnością okaże się przydatna.

Co to są wzory Viète'a?

Wzory Viète'a to zestaw równań wiążących współczynniki wielomianu z sumami i iloczynami jego pierwiastków. Innymi słowy, pozwalają one odczytać pewne informacje o pierwiastkach wielomianu, znając jedynie jego współczynniki, i odwrotnie. Są one niezwykle przydatne w rozwiązywaniu zadań, gdzie nie musimy wyznaczać dokładnych wartości pierwiastków, a jedynie znać pewne relacje między nimi.

Dlaczego nazywają się wzory Viète'a? Nazwane są na cześć francuskiego matematyka François Viète'a, który jako jeden z pierwszych sformułował ogólne zależności między pierwiastkami i współczynnikami równań.

Wzory Viète'a istnieją dla wielomianów dowolnego stopnia, ale w tym artykule skupimy się na wielomianach stopnia trzeciego. Dlaczego? Ponieważ są one wystarczająco złożone, aby pokazać moc tych wzorów, a jednocześnie na tyle proste, aby można je było łatwo zrozumieć i zastosować.

Wzory Viète'a dla wielomianu stopnia trzeciego

Rozważmy ogólną postać wielomianu stopnia trzeciego:

ax³ + bx² + cx + d = 0

Zakładamy, że wielomian ten ma trzy pierwiastki: x₁, x₂ oraz x₃. Wzory Viète'a dla tego wielomianu prezentują się następująco:

Suma pierwiastków: x₁ + x₂ + x₃ = -b/a
Suma iloczynów par pierwiastków: x₁x₂ + x₁x₃ + x₂x₃ = c/a
Iloczyn pierwiastków: x₁x₂x₃ = -d/a

Zauważ, jak proste są te zależności! Współczynniki wielomianu bezpośrednio wiążą się z sumami i iloczynami jego pierwiastków.

Jak zapamiętać te wzory?

Istnieje kilka trików, które mogą pomóc w zapamiętaniu wzorów Viète'a. Oto jeden z nich:

Zwróć uwagę na następujące aspekty:

Znak: Znaki zmieniają się naprzemiennie: minus, plus, minus...
Mianownik: W każdym wzorze w mianowniku znajduje się współczynnik przy najwyższej potędze (w naszym przypadku a).
Licznik: W licznikach występują kolejno współczynniki: b, c, d.
Kolejność: Najpierw mamy sumę wszystkich pierwiastków, potem sumę iloczynów par, a na końcu iloczyn wszystkich pierwiastków.

Pamiętając te zasady, łatwiej odtworzysz wzory Viète'a nawet podczas stresującej sytuacji, np. na egzaminie.

Przykłady zastosowania

Aby lepiej zrozumieć, jak działają wzory Viète'a, przeanalizujmy kilka przykładów.

Przykład 1: Znalezienie sumy kwadratów pierwiastków

Rozważmy wielomian x³ - 6x² + 11x - 6 = 0. Niech x₁, x₂ oraz x₃ będą jego pierwiastkami. Chcemy znaleźć wartość wyrażenia x₁² + x₂² + x₃².

Z wzorów Viète'a mamy:

x₁ + x₂ + x₃ = 6
x₁x₂ + x₁x₃ + x₂x₃ = 11
x₁x₂x₃ = 6

Wykorzystamy teraz tożsamość algebraiczną:

(x₁ + x₂ + x₃)² = x₁² + x₂² + x₃² + 2(x₁x₂ + x₁x₃ + x₂x₃)

Podstawiając znane wartości, otrzymujemy:

6² = x₁² + x₂² + x₃² + 2 * 11

Stąd:

x₁² + x₂² + x₃² = 36 - 22 = 14

Zatem suma kwadratów pierwiastków wynosi 14. Zauważ, że nie musieliśmy wyznaczać wartości poszczególnych pierwiastków!

Przykład 2: Sprawdzanie poprawności pierwiastków

Załóżmy, że wiemy, że pierwiastkami wielomianu x³ - 4x² + x + 6 = 0 są liczby -1, 2 i 3. Czy te pierwiastki są poprawne? Możemy to sprawdzić za pomocą wzorów Viète'a.

Z wzorów Viète'a otrzymujemy:

Suma pierwiastków: -1 + 2 + 3 = 4. Zgodnie ze wzorem: -b/a = -(-4)/1 = 4. Zgadza się!
Suma iloczynów par: (-1)*2 + (-1)*3 + 2*3 = -2 - 3 + 6 = 1. Zgodnie ze wzorem: c/a = 1/1 = 1. Zgadza się!
Iloczyn pierwiastków: (-1)*2*3 = -6. Zgodnie ze wzorem: -d/a = -6/1 = -6. Zgadza się!

Ponieważ wszystkie warunki są spełnione, możemy potwierdzić, że podane pierwiastki są poprawne.

Przykład 3: Znalezienie trzeciego pierwiastka

Wiemy, że wielomian 2x³ + x² - 7x - 6 = 0 ma dwa pierwiastki: -1 oraz 2. Znajdź trzeci pierwiastek.

Oznaczmy trzeci pierwiastek jako x₃. Z wzoru Viète'a na sumę pierwiastków mamy:

-1 + 2 + x₃ = -b/a = -1/2

Stąd:

1 + x₃ = -1/2

x₃ = -1/2 - 1 = -3/2

Zatem trzeci pierwiastek to -3/2.

Kiedy warto korzystać ze wzorów Viète'a?

Wzory Viète'a są szczególnie przydatne w następujących sytuacjach:

Gdy nie potrzebujemy znać dokładnych wartości pierwiastków, a jedynie pewne relacje między nimi (np. suma, iloczyn, suma kwadratów).
Gdy znamy część pierwiastków i chcemy znaleźć pozostałe.
Gdy chcemy sprawdzić, czy podane pierwiastki są poprawne.
Gdy chcemy uprościć zadanie, unikając żmudnego rozwiązywania równania wielomianowego.

Pamiętaj! Wzory Viète'a to tylko narzędzie. Nie zawsze są one najefektywniejszym sposobem rozwiązania danego problemu. Ważne jest, aby umieć ocenić, kiedy warto z nich skorzystać.

Ograniczenia wzorów Viète'a

Wzory Viète'a, mimo swojej użyteczności, mają pewne ograniczenia:

Trudność z pierwiastkami niewymiernymi i zespolonymi: Chociaż wzory działają również dla pierwiastków niewymiernych i zespolonych, obliczenia mogą stać się bardziej skomplikowane.
Brak informacji o typie pierwiastków: Wzory Viète'a same w sobie nie mówią nam, czy pierwiastki są rzeczywiste, zespolone, czy też jakie mają krotności.
Nie zawsze prowadzą do rozwiązania: W niektórych przypadkach, choć możemy użyć wzorów Viète'a, mogą one nie doprowadzić nas do rozwiązania problemu bez dodatkowych technik.

Podsumowanie

Wzory Viète'a to potężne narzędzie, które pozwala zrozumieć i analizować równania wielomianowe stopnia trzeciego. Znajomość tych wzorów pozwala na efektywne rozwiązywanie zadań, w których nie musimy wyznaczać dokładnych wartości pierwiastków, a jedynie znać pewne relacje między nimi. Pamiętaj o prostych zasadach, które pomogą Ci zapamiętać te wzory, i ćwicz ich stosowanie na różnych przykładach. Z czasem staną się one Twoim niezawodnym narzędziem w rozwiązywaniu problemów matematycznych.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć wzory Viète'a i ich zastosowanie. Powodzenia w dalszej nauce matematyki!