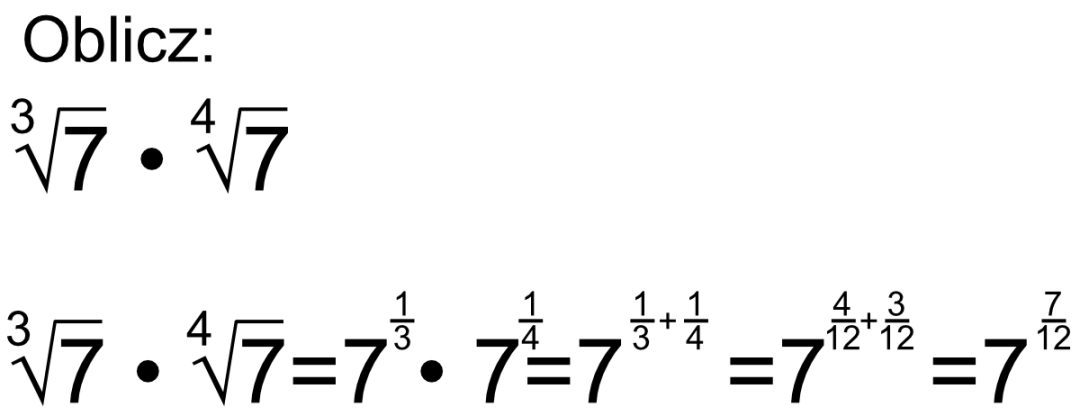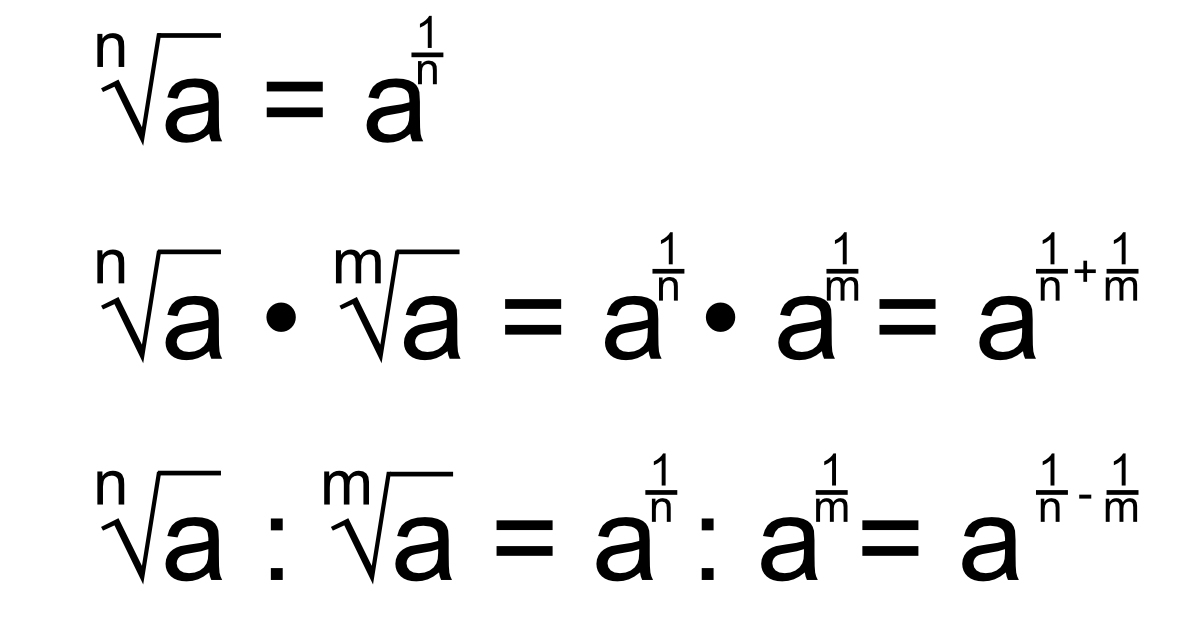Wzory Na Potęgi I Pierwiastki

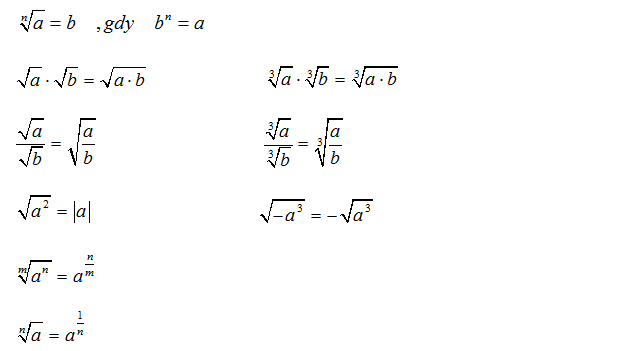
Zarówno potęgi jak i pierwiastki stanowią fundament matematyki, znajdując zastosowanie w wielu dziedzinach nauki i techniki. Zrozumienie ich właściwości i wzorów, które nimi rządzą, jest kluczowe do efektywnego rozwiązywania problemów matematycznych i modelowania rzeczywistych zjawisk. Ten artykuł ma na celu usystematyzowanie wiedzy na temat potęg i pierwiastków, prezentując najważniejsze wzory i ich praktyczne zastosowania.

Wprowadzenie do Potęg

Potęgowanie to operacja matematyczna, która polega na mnożeniu liczby przez samą siebie określoną liczbę razy. Liczbę, którą mnożymy, nazywamy podstawą potęgi, a liczbę, która określa, ile razy mnożymy podstawę przez samą siebie, nazywamy wykładnikiem potęgi. Zapis aⁿ oznacza, że liczbę a (podstawa) podnosimy do potęgi n (wykładnik).

Podstawowe Wzory na Potęgi

Poniżej przedstawiamy najważniejsze wzory dotyczące potęg:

a^m * aⁿ = a^m+n - Mnożenie potęg o tej samej podstawie. Wykladniki dodajemy. Przykład: 2³ * 2² = 2³⁺² = 2⁵ = 32
a^m / aⁿ = a^m-n - Dzielenie potęg o tej samej podstawie. Wykladniki odejmujemy. Przykład: 3⁵ / 3² = 3^5-2 = 3³ = 27
(a^m)ⁿ = a^m*n - Potęgowanie potęgi. Wykładniki mnożymy. Przykład: (5²)³ = 5^2*3 = 5⁶ = 15625
(a * b)ⁿ = aⁿ * bⁿ - Potęgowanie iloczynu. Potęgujemy każdy czynnik. Przykład: (2 * 3)² = 2² * 3² = 4 * 9 = 36
(a / b)ⁿ = aⁿ / bⁿ - Potęgowanie ilorazu. Potęgujemy licznik i mianownik. Przykład: (4 / 2)³ = 4³ / 2³ = 64 / 8 = 8
a⁰ = 1 (dla a ≠ 0) - Dowolna liczba (różna od zera) podniesiona do potęgi zerowej daje 1. Przykład: 7⁰ = 1
a^-n = 1 / aⁿ - Potęga o wykładniku ujemnym. Przykład: 2^-3 = 1 / 2³ = 1 / 8

Przykłady Zastosowań Potęg

Potęgi mają szerokie zastosowanie w różnych dziedzinach. Oto kilka przykładów:

Informatyka: W informatyce potęgi są używane do określania rozmiaru pamięci komputerowej (np. kilobajty, megabajty, gigabajty) oraz do reprezentacji liczb binarnych. Na przykład, 2¹⁰ bajtów to 1 kilobajt (KB).
Finanse: W finansach potęgi są używane do obliczania procentu składanego. Wzór na wartość przyszłą kapitału (FV) po n latach, przy stopie procentowej r, to FV = PV * (1 + r)ⁿ, gdzie PV to wartość początkowa kapitału.
Fizyka: W fizyce potęgi występują w wielu wzorach, np. wzór na energię kinetyczną (E_k = (1/2)mv²), gdzie prędkość (v) jest podnoszona do kwadratu.
Biologia: W biologii potęgi mogą modelować wzrost populacji. Na przykład, wzrost bakterii może być opisywany funkcją eksponencjalną, gdzie potęga jest związana z czasem.

Wprowadzenie do Pierwiastków

Pierwiastkowanie to operacja odwrotna do potęgowania. Pierwiastek stopnia n z liczby a, oznaczany jako ⁿ√a, to taka liczba b, że bⁿ = a. Na przykład, ²√9 = 3, ponieważ 3² = 9. Pierwiastek stopnia 2 nazywamy pierwiastkiem kwadratowym, a pierwiastek stopnia 3 nazywamy pierwiastkiem sześciennym.

Podstawowe Wzory na Pierwiastki

Poniżej przedstawiamy najważniejsze wzory dotyczące pierwiastków:

ⁿ√(a * b) = ⁿ√a * ⁿ√b - Pierwiastek z iloczynu. Możemy rozdzielić pierwiastek na czynniki. Przykład: ³√(8 * 27) = ³√8 * ³√27 = 2 * 3 = 6
ⁿ√(a / b) = ⁿ√a / ⁿ√b - Pierwiastek z ilorazu. Możemy rozdzielić pierwiastek na licznik i mianownik. Przykład: ²√(16 / 4) = ²√16 / ²√4 = 4 / 2 = 2
^m√ⁿ√a = ^m*n√a - Pierwiastek z pierwiastka. Stopnie pierwiastków mnożymy. Przykład: ²√³√64 = ^2*3√64 = ⁶√64 = 2
(ⁿ√a)^m = ⁿ√(a^m) - Potęgowanie pierwiastka. Możemy potęgować liczbę pod pierwiastkiem. Przykład: (²√4)³ = ²√(4³) = ²√64 = 8
ⁿ√aⁿ = a (dla a ≥ 0, jeśli n parzyste) - Pierwiastek stopnia n z liczby podniesionej do potęgi n (dla a nieujemnego, jeśli n jest parzyste). Przykład: ³√5³ = 5

Związek Pierwiastków z Potęgami

Pierwiastki można wyrazić za pomocą potęg o wykładniku ułamkowym:

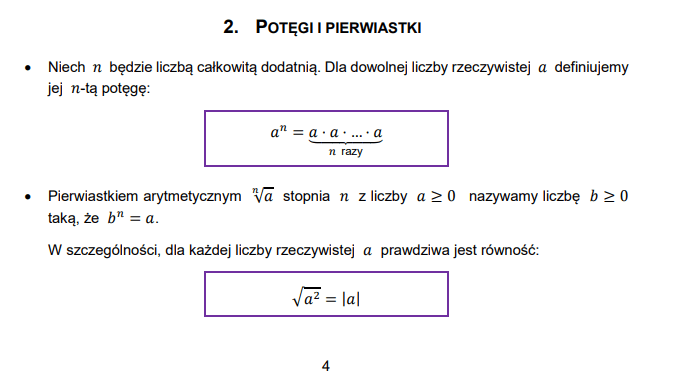
ⁿ√a = a^1/n - Pierwiastek stopnia n to potęga o wykładniku 1/n. Przykład: ²√9 = 9^1/2 = 3

Wykorzystanie tego związku pozwala na stosowanie wzorów na potęgi do operacji na pierwiastkach.

Przykłady Zastosowań Pierwiastków

Podobnie jak potęgi, pierwiastki mają liczne zastosowania w różnych dziedzinach:

Geometria: W geometrii pierwiastki są używane do obliczania długości boków, przekątnych i promieni w figurach geometrycznych. Na przykład, długość przekątnej kwadratu o boku a wynosi a√2.
Fizyka: W fizyce pierwiastki występują we wzorach na prędkość, energię i inne wielkości fizyczne. Na przykład, okres drgań wahadła matematycznego T = 2π√(l/g), gdzie l to długość wahadła, a g to przyspieszenie ziemskie.
Statystyka: W statystyce pierwiastek kwadratowy z wariancji nazywany jest odchyleniem standardowym, które mierzy rozproszenie danych wokół średniej.
Inżynieria: W inżynierii pierwiastki są używane do rozwiązywania równań i modelowania różnych systemów.

Zaawansowane Operacje i Przekształcenia

Zrozumienie podstawowych wzorów na potęgi i pierwiastki pozwala na wykonywanie bardziej zaawansowanych operacji i przekształceń. Na przykład, można upraszczać wyrażenia zawierające potęgi i pierwiastki, doprowadzając je do prostszej postaci.

Przykład upraszczania wyrażenia: √(x³ * y²) = √(x² * x * y²) = x * y * √x, zakładając, że x i y są nieujemne.

W rozwiązywaniu równań, wykorzystywanie właściwości potęg i pierwiastków jest często kluczowe do znalezienia rozwiązania. Przykładowo, rozwiązując równanie x² = 9, pierwiastkujemy obie strony, otrzymując x = ±3.

Podsumowanie

Potęgi i pierwiastki są fundamentalnymi operacjami matematycznymi, które znajdują szerokie zastosowanie w różnych dziedzinach nauki i techniki. Zrozumienie i opanowanie wzorów, które nimi rządzą, jest niezbędne do efektywnego rozwiązywania problemów i modelowania rzeczywistych zjawisk. Pamiętaj ćwiczenie czyni mistrza! Regularne rozwiązywanie zadań pozwoli na utrwalenie wiedzy i rozwijanie umiejętności w zakresie operacji na potęgach i pierwiastkach.

Zachęcamy do dalszego zgłębiania wiedzy na temat potęg i pierwiastków, korzystania z dostępnych zasobów edukacyjnych i rozwiązywania różnorodnych zadań. Im lepiej zrozumiesz te koncepcje, tym łatwiej będzie Ci radzić sobie z bardziej złożonymi problemami matematycznymi.