Wzory Na Pola I Obwody Figur Płaskich
Hej Uczniu! Przygotowujesz się do egzaminu z geometrii? Świetnie! Pamiętaj, że kluczem do sukcesu jest solidna znajomość wzorów na pola i obwody figur płaskich. Nie martw się, jeśli czujesz się trochę zagubiony – jestem tutaj, żeby Ci pomóc! Przejdziemy przez wszystkie najważniejsze figury krok po kroku, a na koniec podsumujemy wszystko, żebyś miał/a jasny obraz sytuacji. Dasz radę!
Podstawy: Trójkąty
Zaczynamy od trójkątów, bo to fundament wielu innych figur. Pamiętaj, że trójkąt może mieć różne kształty, ale zasada obliczania pola zawsze jest podobna.
Pole trójkąta
Podstawowy wzór na pole trójkąta to:
P = (1/2) * a * h
Gdzie:
- P to pole trójkąta
- a to długość podstawy trójkąta
- h to wysokość trójkąta, opuszczona na tę podstawę
Ważne: Wysokość zawsze musi być prostopadła do podstawy!
Jeśli znasz długości dwóch boków trójkąta (a i b) oraz kąt między nimi (γ), możesz użyć wzoru:
P = (1/2) * a * b * sin(γ)
Dla trójkąta równobocznego (wszystkie boki równe a) wzór na pole upraszcza się do:
P = (a2 * √3) / 4
A jeśli znasz długości wszystkich trzech boków trójkąta (a, b, c), możesz skorzystać ze wzoru Herona:
P = √(p * (p - a) * (p - b) * (p - c))
Gdzie p to połowa obwodu trójkąta: p = (a + b + c) / 2
Obwód trójkąta
Obwód trójkąta to po prostu suma długości wszystkich jego boków:
Obwód = a + b + c
Kwadraty i Prostokąty
Teraz przejdźmy do czworokątów.
Kwadrat
Kwadrat to szczególny przypadek prostokąta, gdzie wszystkie boki są równe (oznaczmy je jako a).
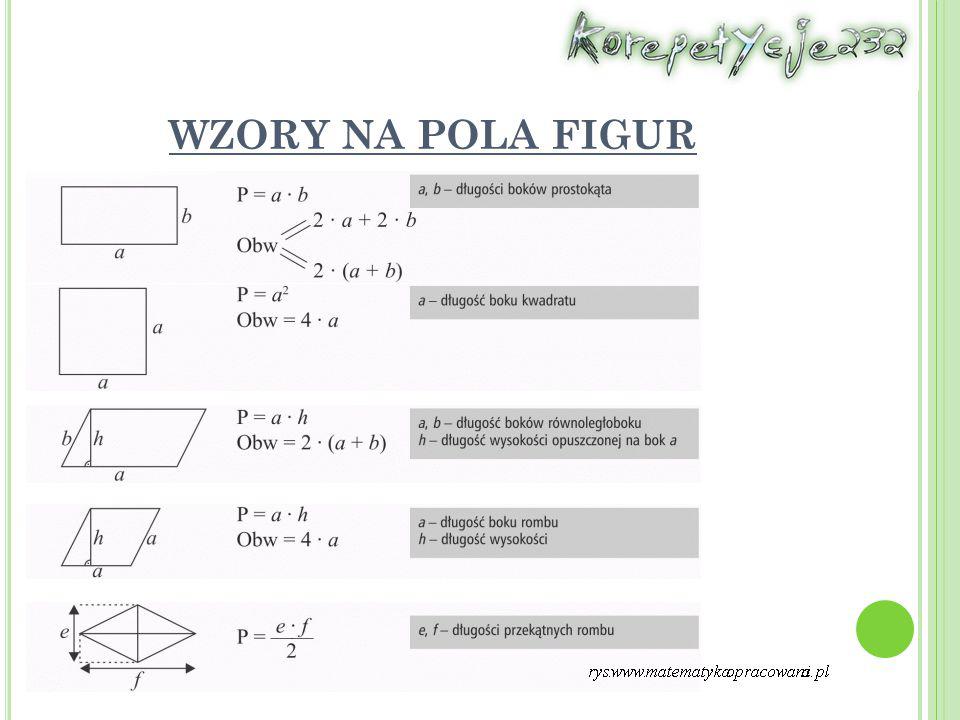
Pole kwadratu:
P = a2
Obwód kwadratu:
Obwód = 4 * a
Prostokąt
Prostokąt ma dwa boki o długości a i dwa boki o długości b.
Pole prostokąta:
P = a * b
Obwód prostokąta:
Obwód = 2 * a + 2 * b
Równoległobok i Romb
Równoległobok
Równoległobok ma dwie pary boków równoległych. Podobnie jak w trójkącie, potrzebujemy podstawy (a) i wysokości (h) opuszczonej na tę podstawę.
Pole równoległoboku:
P = a * h
Obwód równoległoboku:
Obwód = 2 * a + 2 * b (gdzie a i b to długości sąsiednich boków)
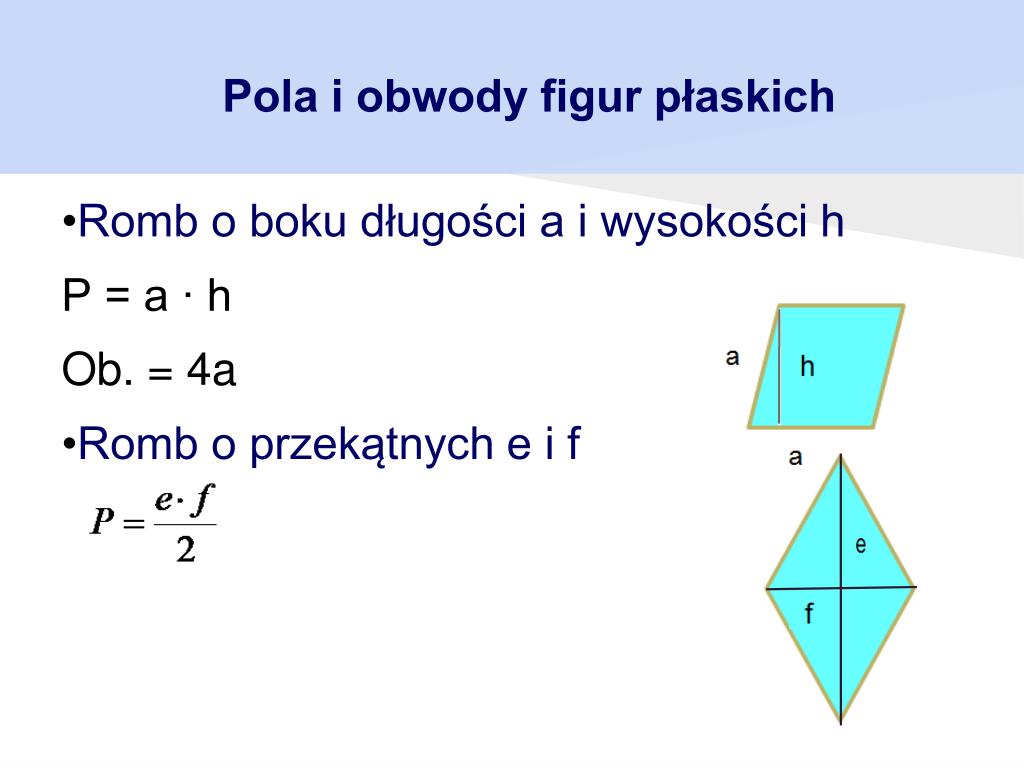
Romb
Romb to równoległobok, który ma wszystkie boki równe (a). Możemy obliczyć jego pole na dwa sposoby:
1. Używając podstawy i wysokości:
P = a * h
2. Używając długości przekątnych (d1 i d2):
P = (1/2) * d1 * d2
Obwód rombu:
Obwód = 4 * a
Trapez
Trapez ma dwa boki równoległe (podstawy a i b) oraz dwa boki nierównoległe.
Pole trapezu:
P = (1/2) * (a + b) * h
Gdzie h to wysokość trapezu (odległość między podstawami).
Obwód trapezu:
Obwód = a + b + c + d (gdzie a i b to podstawy, a c i d to długości pozostałych boków)
Koło
Ostatnia figura na naszej liście to koło. Potrzebujemy znać tylko promień (r).
Pole koła:
P = π * r2
Obwód koła (długość okręgu):
Obwód = 2 * π * r
Pamiętaj, że π (pi) to stała matematyczna, w przybliżeniu równa 3.14159.
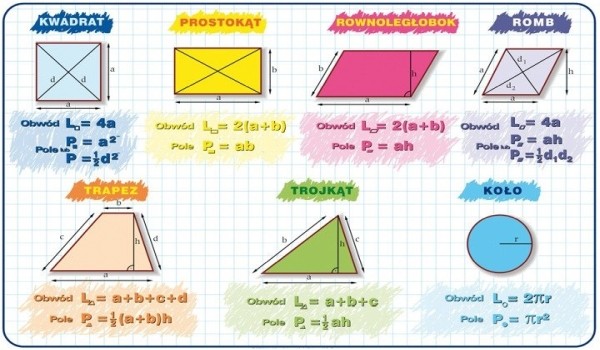
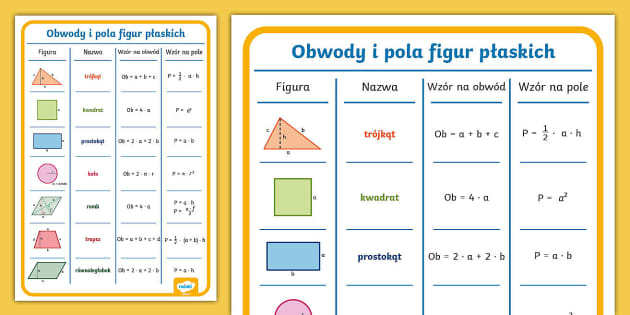
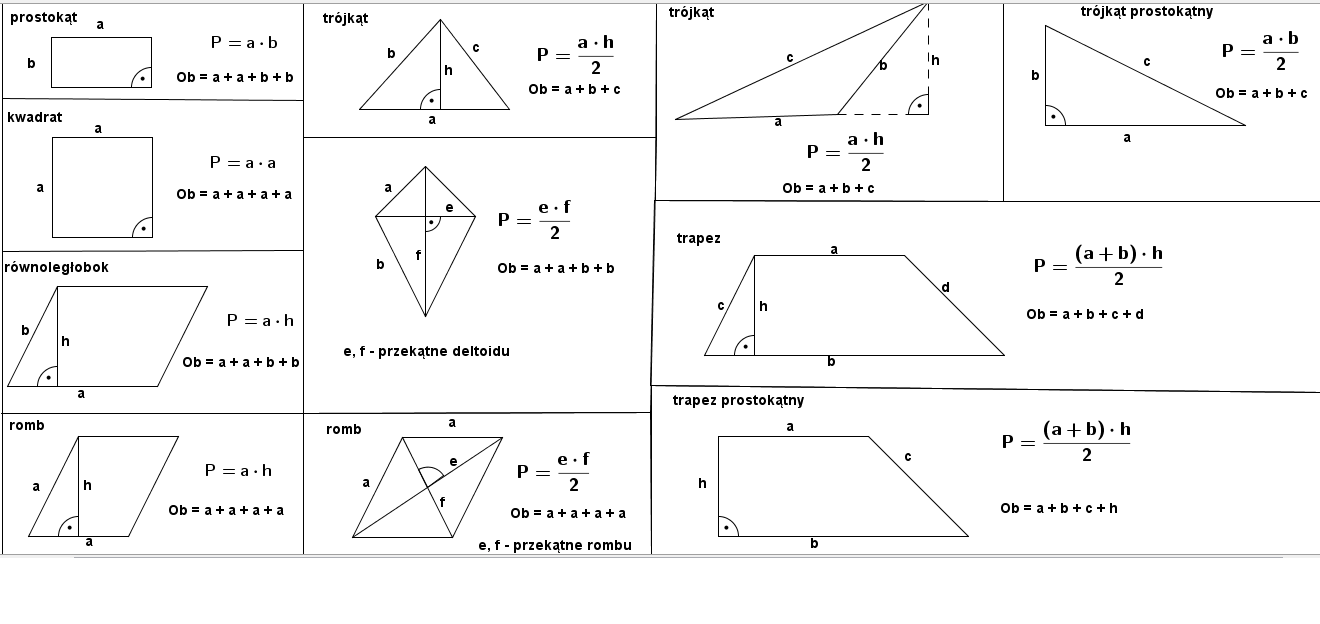
Podsumowanie Kluczowych Wzorów
Żebyś miał/a wszystko w jednym miejscu, spójrzmy na krótkie podsumowanie najważniejszych wzorów:
- Trójkąt: P = (1/2) * a * h, Obwód = a + b + c
- Kwadrat: P = a2, Obwód = 4 * a
- Prostokąt: P = a * b, Obwód = 2 * a + 2 * b
- Równoległobok: P = a * h, Obwód = 2 * a + 2 * b
- Romb: P = a * h lub P = (1/2) * d1 * d2, Obwód = 4 * a
- Trapez: P = (1/2) * (a + b) * h, Obwód = a + b + c + d
- Koło: P = π * r2, Obwód = 2 * π * r
Pamiętaj, żeby zrozumieć, co oznaczają poszczególne litery we wzorach i kiedy ich używać. Rozwiązuj zadania i ćwicz, ćwicz, ćwicz! Im więcej będziesz ćwiczyć, tym łatwiej zapamiętasz wzory i nauczysz się je stosować. Powodzenia na egzaminie! Wierzę w Ciebie!