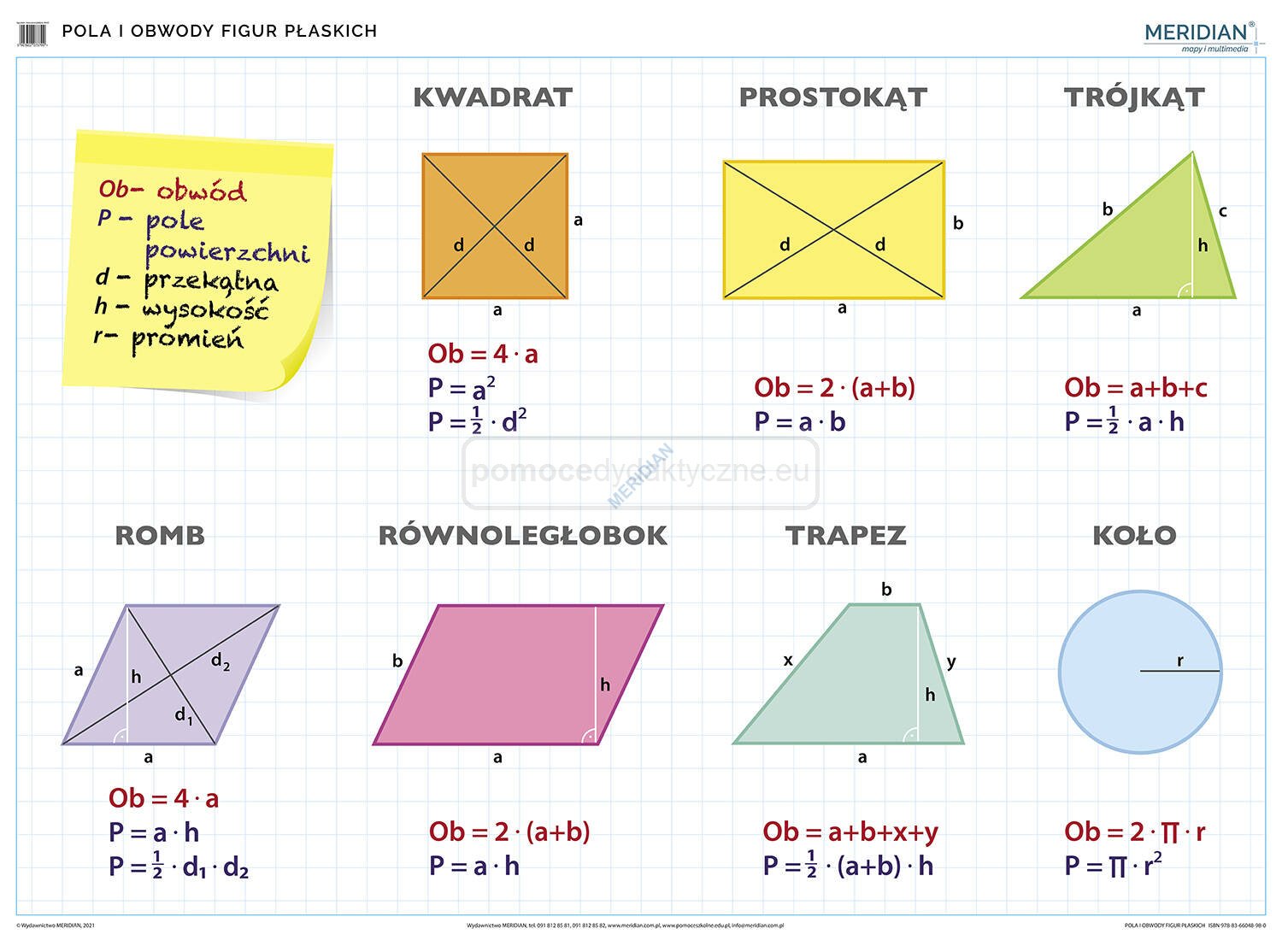
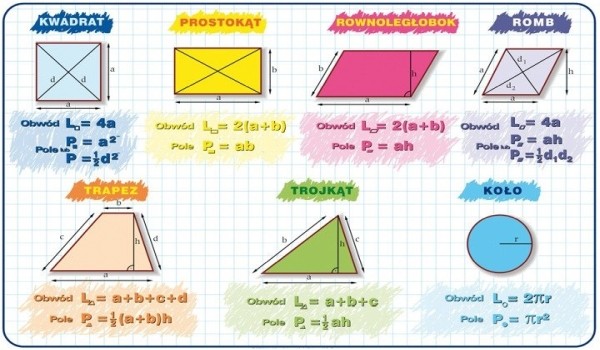
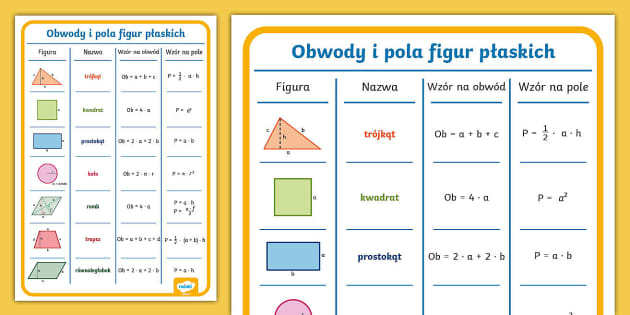
Wzory Na Pola I Obwody Figur

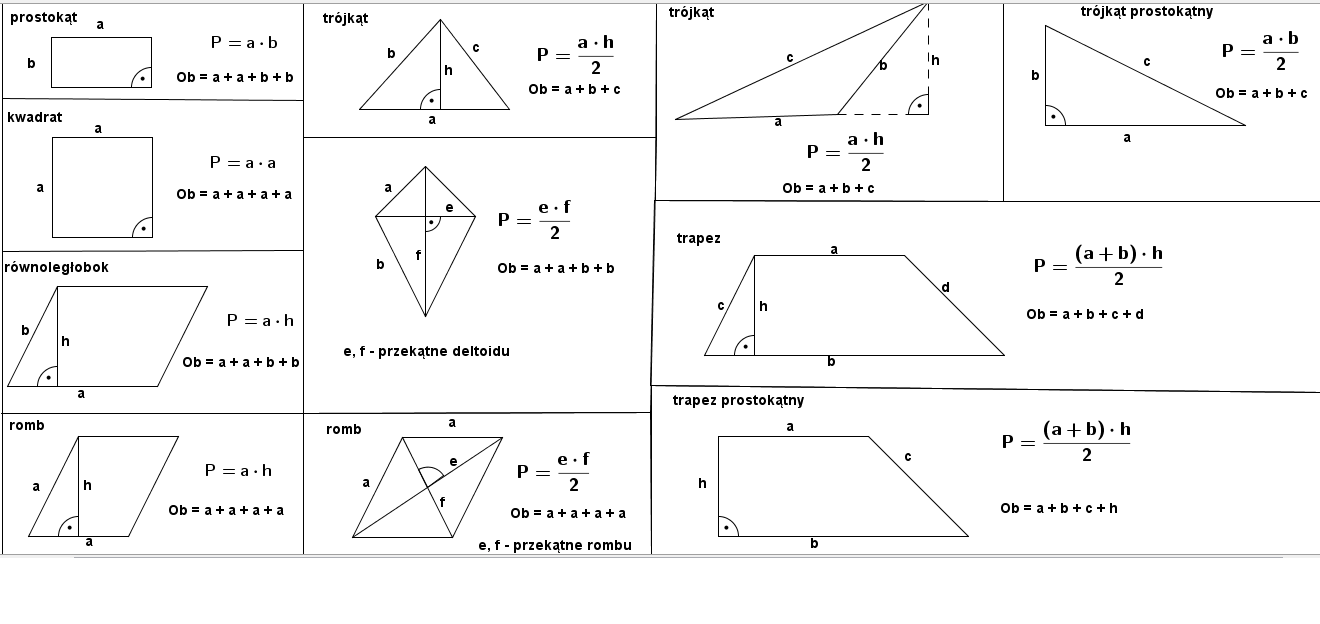
Czy kiedykolwiek zastanawiałeś się, jak obliczyć powierzchnię swojego pokoju przed zakupem nowej podłogi? A może potrzebujesz znać obwód rabaty kwiatowej, żeby wiedzieć, ile siatki ochronnej kupić? Jeśli tak, to ten artykuł jest dla Ciebie! Zrozumienie wzorów na pola i obwody figur geometrycznych może wydawać się trudne, ale z nami stanie się to proste i przyjemne. Pokażemy Ci, jak to zrobić krok po kroku, używając jasnych przykładów i unikając zbędnego żargonu.

Dlaczego Wzory na Pola i Obwody Są Ważne?

Wzory na pola i obwody figur geometrycznych to nie tylko suche formułki z podręcznika. Mają one realne zastosowanie w naszym codziennym życiu. Od planowania remontu, przez projektowanie ogrodu, aż po rozwiązywanie problemów w pracy - umiejętność obliczania pól i obwodów jest niezwykle przydatna.

Według badań przeprowadzonych przez Uniwersytet Warszawski, osoby posiadające dobrą znajomość geometrii przestrzennej lepiej radzą sobie z problemami wymagającymi logicznego myślenia i planowania. To pokazuje, że inwestycja w zrozumienie tych podstawowych zagadnień procentuje w wielu dziedzinach życia.

Podstawowe Figury i Wzory

Zacznijmy od podstawowych figur geometrycznych i wzorów, które musisz znać.

Kwadrat

Kwadrat to figura o czterech równych bokach i czterech kątach prostych.

Pole (P): P = a² (gdzie 'a' to długość boku)
Obwód (O): O = 4a

Przykład: Kwadrat ma bok długości 5 cm. Jego pole wynosi 5² = 25 cm², a obwód 4 * 5 = 20 cm.

Prostokąt

Prostokąt ma dwa boki o różnych długościach i cztery kąty proste.

Pole (P): P = a * b (gdzie 'a' i 'b' to długości boków)
Obwód (O): O = 2a + 2b

Przykład: Prostokąt ma boki o długości 3 cm i 7 cm. Jego pole wynosi 3 * 7 = 21 cm², a obwód 2 * 3 + 2 * 7 = 20 cm.

Trójkąt

Trójkąt to figura o trzech bokach. Istnieje wiele rodzajów trójkątów (równoboczny, równoramienny, prostokątny), ale wzór na pole jest ogólny:

Pole (P): P = 0.5 * a * h (gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę)
Obwód (O): O = a + b + c (gdzie 'a', 'b' i 'c' to długości boków)

Przykład: Trójkąt ma podstawę o długości 8 cm i wysokość opuszczoną na tę podstawę o długości 6 cm. Jego pole wynosi 0.5 * 8 * 6 = 24 cm². Jeśli boki trójkąta mają długości 8 cm, 7 cm i 5 cm, to jego obwód wynosi 8 + 7 + 5 = 20 cm.

Równoległobok

Równoległobok to czworokąt, którego przeciwległe boki są równoległe.

Pole (P): P = a * h (gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę)
Obwód (O): O = 2a + 2b (gdzie 'a' i 'b' to długości boków)

Przykład: Równoległobok ma podstawę o długości 10 cm i wysokość opuszczoną na tę podstawę o długości 4 cm. Jego pole wynosi 10 * 4 = 40 cm². Jeśli boki równoległoboku mają długości 10 cm i 6 cm, to jego obwód wynosi 2 * 10 + 2 * 6 = 32 cm.

Trapez

Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych (zwanych podstawami).

Pole (P): P = 0.5 * (a + b) * h (gdzie 'a' i 'b' to długości podstaw, a 'h' to wysokość)
Obwód (O): O = a + b + c + d (gdzie 'a', 'b' to długości podstaw, a 'c' i 'd' to długości pozostałych boków)

Przykład: Trapez ma podstawy o długościach 5 cm i 9 cm, a wysokość 4 cm. Jego pole wynosi 0.5 * (5 + 9) * 4 = 28 cm². Jeśli boki trapezu mają długości 5 cm, 9 cm, 3 cm i 4 cm, to jego obwód wynosi 5 + 9 + 3 + 4 = 21 cm.

Koło

Koło to figura, której wszystkie punkty są w równej odległości od środka.

Pole (P): P = πr² (gdzie 'r' to promień koła, a π (pi) to stała matematyczna, w przybliżeniu równa 3.14)
Obwód (O) - inaczej długość okręgu: O = 2πr

Przykład: Koło ma promień o długości 4 cm. Jego pole wynosi π * 4² ≈ 3.14 * 16 = 50.24 cm², a obwód (długość okręgu) 2 * π * 4 ≈ 2 * 3.14 * 4 = 25.12 cm.

Praktyczne Zastosowania

Jak już wspomnieliśmy, wzory na pola i obwody mają szerokie zastosowanie w życiu codziennym. Oto kilka przykładów:

Remont mieszkania: Obliczanie powierzchni ścian i podłóg, aby określić, ile farby, tapety czy paneli podłogowych potrzebujesz.
Ogród: Planowanie rabat kwiatowych, obliczanie ilości siatki potrzebnej do ogrodzenia, czy określanie, ile nawozu potrzebujesz na dany obszar.
Gotowanie: Określanie ilości ciasta potrzebnej do wyłożenia formy o danym kształcie i rozmiarze.
Szycie: Obliczanie ilości materiału potrzebnej do uszycia ubrania o określonym kroju.

Wskazówki i Triki

Oto kilka wskazówek, które mogą Ci pomóc w obliczaniu pól i obwodów:

Zawsze zwracaj uwagę na jednostki: Upewnij się, że wszystkie wymiary są wyrażone w tej samej jednostce (np. cm, m, mm).
Rysuj diagramy: Narysowanie figury, której pole lub obwód chcesz obliczyć, może pomóc Ci lepiej zrozumieć problem i uniknąć błędów.
Sprawdzaj swoje obliczenia: Zawsze sprawdź swoje obliczenia, aby upewnić się, że nie popełniłeś błędu. Możesz użyć kalkulatora online lub poprosić kogoś o sprawdzenie Twoich wyników.
Korzystaj z kalkulatorów online: Istnieje wiele darmowych kalkulatorów online, które mogą pomóc Ci w obliczaniu pól i obwodów figur geometrycznych.

Pamiętaj, że praktyka czyni mistrza! Im więcej będziesz ćwiczył obliczanie pól i obwodów, tym łatwiej i szybciej będziesz to robił.

Podsumowanie

Wzory na pola i obwody figur geometrycznych to podstawa wielu dziedzin życia. Zrozumienie ich i umiejętność ich stosowania pozwala nam lepiej planować, rozwiązywać problemy i radzić sobie w różnych sytuacjach. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć te zagadnienia i że teraz obliczanie pól i obwodów będzie dla Ciebie proste i przyjemne.

Jeśli masz jakieś pytania lub wątpliwości, nie wahaj się ich zadać!