Wzory Na Pola Figur Przestrzennych

Czy kiedykolwiek zastanawiałeś się, ile farby potrzebujesz, żeby pomalować gigantyczną piłkę? Albo ile wody zmieści się w basenie o nietypowym kształcie? Odpowiedzi na te (i wiele innych) pytania kryją się w wzorach na pola i objętości figur przestrzennych. Ten artykuł jest właśnie dla Ciebie – ucznia, studenta, majsterkowicza lub po prostu osoby ciekawej świata, która chce zrozumieć podstawy geometrii 3D.

Wprowadzenie do Figur Przestrzennych

Figury przestrzenne, zwane również bryłami, to obiekty, które zajmują miejsce w trójwymiarowej przestrzeni. W przeciwieństwie do figur płaskich, które mają tylko długość i szerokość, bryły mają również wysokość, głębokość lub grubość. Codziennie spotykamy się z bryłami: piłka, pudełko, budynek – to wszystko figury przestrzenne.

Zrozumienie, jak obliczać pola powierzchni i objętości tych figur, jest kluczowe w wielu dziedzinach, od architektury i inżynierii, po projektowanie gier komputerowych i grafikę 3D.

Dlaczego warto znać te wzory?

Praktyczne zastosowania: Potrzebujesz oszacować ilość materiału do budowy, obliczyć pojemność zbiornika, czy zrozumieć, jak optymalnie zapakować przedmioty? Znajomość wzorów na pola i objętości brył jest nieoceniona.
Rozwijanie myślenia przestrzennego: Praca z geometrią przestrzenną rozwija wyobraźnię i zdolność do wizualizacji obiektów w trzech wymiarach.
Podstawa do dalszej nauki: Zrozumienie tych podstawowych koncepcji jest niezbędne do dalszej nauki matematyki, fizyki i innych nauk ścisłych.

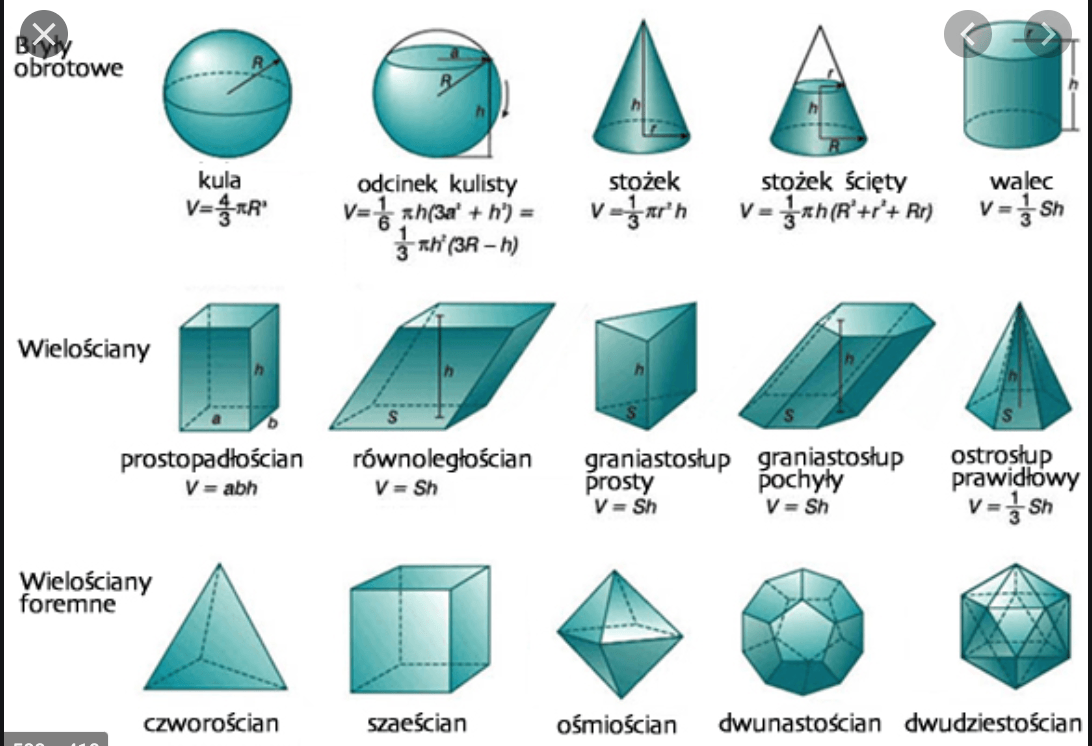
Podstawowe Figury Przestrzenne i Ich Wzory

Przyjrzyjmy się teraz najpopularniejszym figurom przestrzennym i wzorom na obliczanie ich pola powierzchni całkowitej (Pc) oraz objętości (V).

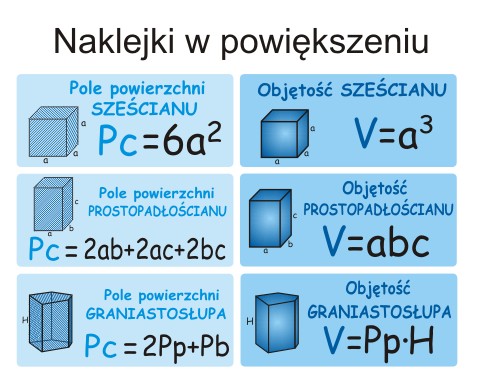
Sześcian

Sześcian to prostopadłościan, którego wszystkie krawędzie są równe. Jest to jedna z najprostszych i najczęściej spotykanych brył.

Oznaczenia: a – długość krawędzi
Wzór na pole powierzchni całkowitej: Pc = 6a²
Wzór na objętość: V = a³

Przykład: Sześcian ma krawędź o długości 5 cm. Oblicz jego pole powierzchni całkowitej i objętość. * Pc = 6 * 5² = 6 * 25 = 150 cm² * V = 5³ = 125 cm³

Prostopadłościan

Prostopadłościan to bryła, której wszystkie ściany są prostokątami.

Oznaczenia: a, b, c – długości krawędzi
Wzór na pole powierzchni całkowitej: Pc = 2(ab + bc + ac)
Wzór na objętość: V = abc

Przykład: Prostopadłościan ma krawędzie o długości 3 cm, 4 cm i 5 cm. Oblicz jego pole powierzchni całkowitej i objętość. * Pc = 2 * (3*4 + 4*5 + 3*5) = 2 * (12 + 20 + 15) = 2 * 47 = 94 cm² * V = 3 * 4 * 5 = 60 cm³

Walec

Walec to bryła, która powstaje przez obrót prostokąta wokół jednego z jego boków. Charakteryzuje się dwoma podstawami w kształcie kół i powierzchnią boczną, która po rozwinięciu tworzy prostokąt.

Oznaczenia: r – promień podstawy, h – wysokość walca
Wzór na pole powierzchni całkowitej: Pc = 2πr² + 2πrh
Wzór na objętość: V = πr²h

Przykład: Walec ma promień podstawy 2 cm i wysokość 6 cm. Oblicz jego pole powierzchni całkowitej i objętość. * Pc = 2 * π * 2² + 2 * π * 2 * 6 = 8π + 24π = 32π cm² (około 100.53 cm²) * V = π * 2² * 6 = 24π cm³ (około 75.40 cm³)

Stożek

Stożek to bryła, która powstaje przez połączenie punktu (wierzchołka) z okręgiem (podstawą). Ma jedną podstawę w kształcie koła i powierzchnię boczną.

Oznaczenia: r – promień podstawy, h – wysokość stożka, l – tworząca stożka
Wzór na pole powierzchni całkowitej: Pc = πr² + πrl
Wzór na objętość: V = (1/3)πr²h

Przykład: Stożek ma promień podstawy 3 cm, wysokość 4 cm. Oblicz jego pole powierzchni całkowitej i objętość. Najpierw musimy obliczyć tworzącą (l) korzystając z twierdzenia Pitagorasa: l² = r² + h², czyli l² = 3² + 4² = 9 + 16 = 25, więc l = 5 cm. * Pc = π * 3² + π * 3 * 5 = 9π + 15π = 24π cm² (około 75.40 cm²) * V = (1/3) * π * 3² * 4 = (1/3) * π * 9 * 4 = 12π cm³ (około 37.70 cm³)

Kula

Kula to zbiór wszystkich punktów w przestrzeni, które znajdują się w równej odległości od danego punktu (środka kuli).

Oznaczenia: r – promień kuli
Wzór na pole powierzchni: Pc = 4πr²
Wzór na objętość: V = (4/3)πr³

Przykład: Kula ma promień 4 cm. Oblicz jej pole powierzchni i objętość. * Pc = 4 * π * 4² = 4 * π * 16 = 64π cm² (około 201.06 cm²) * V = (4/3) * π * 4³ = (4/3) * π * 64 = (256/3)π cm³ (około 268.08 cm³)

Ostrosłup

Ostrosłup to bryła, której podstawą jest wielokąt, a ściany boczne są trójkątami zbiegającymi się w jednym punkcie (wierzchołku ostrosłupa).

Oznaczenia: Pp - pole podstawy, h - wysokość ostrosłupa, Pb - pole powierzchni bocznej.
Wzór na pole powierzchni całkowitej: Pc = Pp + Pb
Wzór na objętość: V = (1/3) * Pp * h

Graniastosłup

Graniastosłup to bryła, której podstawy są przystającymi wielokątami leżącymi w równoległych płaszczyznach, a ściany boczne są równoległobokami.

Oznaczenia: Pp - pole podstawy, h - wysokość graniastosłupa, Pb - pole powierzchni bocznej.
Wzór na pole powierzchni całkowitej: Pc = 2Pp + Pb
Wzór na objętość: V = Pp * h

Wskazówki i Triki

Zapamiętywanie wzorów: Nie musisz uczyć się wszystkich wzorów na pamięć! Skup się na zrozumieniu, *skąd* się one biorą. Pamiętaj, że wiele z nich wynika z podstawowych zależności geometrycznych.
Jednostki: Zawsze zwracaj uwagę na jednostki! Jeśli długości są podane w centymetrach, pole powierzchni będzie w centymetrach kwadratowych, a objętość w centymetrach sześciennych.
Rozwiązywanie zadań: Najlepszym sposobem na opanowanie wzorów jest rozwiązywanie zadań. Im więcej przykładów przeanalizujesz, tym lepiej zrozumiesz zastosowanie tych wzorów.
Wizualizacja: Staraj się wizualizować bryły w przestrzeni. Pomoże Ci to zrozumieć, które wymiary są istotne i jak wpływają one na pole powierzchni i objętość.

Zastosowania w życiu codziennym

Pomyśl o sytuacjach, w których możesz wykorzystać wiedzę o polach i objętościach figur przestrzennych:

Gotowanie: Obliczanie objętości składników, aby dopasować przepis do większej liczby osób.
Ogrodnictwo: Określanie, ile ziemi potrzebujesz do wypełnienia donicy.
Majsterkowanie: Szacowanie ilości farby, tapety lub materiałów budowlanych potrzebnych do remontu.
Podróże: Optymalne pakowanie walizki, aby zmieścić jak najwięcej rzeczy.

Podsumowanie

W tym artykule omówiliśmy podstawowe figury przestrzenne i wzory na obliczanie ich pola powierzchni i objętości. Mam nadzieję, że teraz, gdy widzisz sześcian, walec, stożek czy kulę, będziesz potrafił oszacować ich wymiary i zrozumieć, jak obliczyć ich pole i objętość. Pamiętaj, geometria jest wszędzie wokół nas, a zrozumienie jej podstaw może ułatwić nam życie i rozwinąć nasze umiejętności myślenia przestrzennego.

Zachęcamy do dalszego eksplorowania fascynującego świata geometrii! Wykorzystaj tę wiedzę w praktyce, rozwiązuj zadania i odkrywaj nowe zastosowania wzorów na pola i objętości figur przestrzennych. Powodzenia!