Wzory Na Pola Figur Płaskich

Czy kiedykolwiek zastanawiałeś się, ile farby potrzebujesz, żeby pomalować ścianę w pokoju? Albo ile materiału zużyjesz na uszycie spódnicy? A może planujesz ułożyć kostkę brukową na podjeździe i chcesz dokładnie wyliczyć, ile jej kupić? W każdym z tych przypadków, znajomość wzorów na pola figur płaskich okazuje się niezwykle przydatna. To nie tylko sucha teoria z podręcznika do matematyki, ale przede wszystkim praktyczne narzędzie, które pomaga nam rozwiązywać problemy w realnym świecie.

Dlaczego Warto Znać Wzory na Pola Figur Płaskich?

Pomyślmy o tym przez chwilę. Bez tej wiedzy, wszystko staje się szacowaniem i przypuszczeniami, co często prowadzi do marnowania materiałów, czasu i pieniędzy. Dzięki wzorom, możemy precyzyjnie obliczyć potrzebną ilość, zminimalizować straty i uniknąć niepotrzebnych kosztów. Ale to nie wszystko!

Praktyczne Zastosowania w Życiu Codziennym:

• Remont i Budowa: Obliczanie powierzchni ścian, podłóg, dachów – niezbędne do zakupu materiałów.
• Ogrodnictwo: Wyznaczanie powierzchni trawnika, klombu, rabaty – kluczowe przy planowaniu i zakupie nasion, sadzonek czy nawozów.
• Krawiectwo: Obliczanie ilości materiału potrzebnego na uszycie ubrania.
• Dekoracja Wnętrz: Dobór odpowiedniego rozmiaru dywanu, obrazu czy plakatu.
• Geodezja i Kartografia: Pomiar i obliczanie powierzchni działek, obszarów, regionów.

To tylko kilka przykładów. W gruncie rzeczy, znajomość wzorów na pola figur płaskich wpływa na efektywność i ekonomię wielu naszych działań.

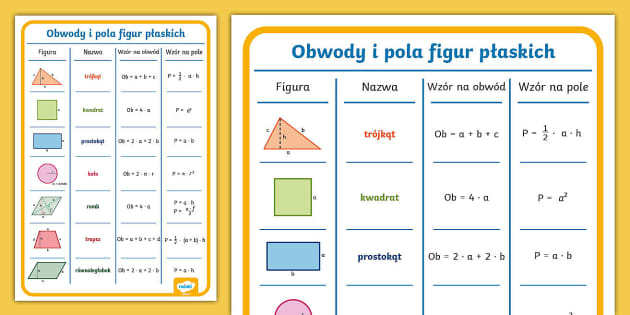
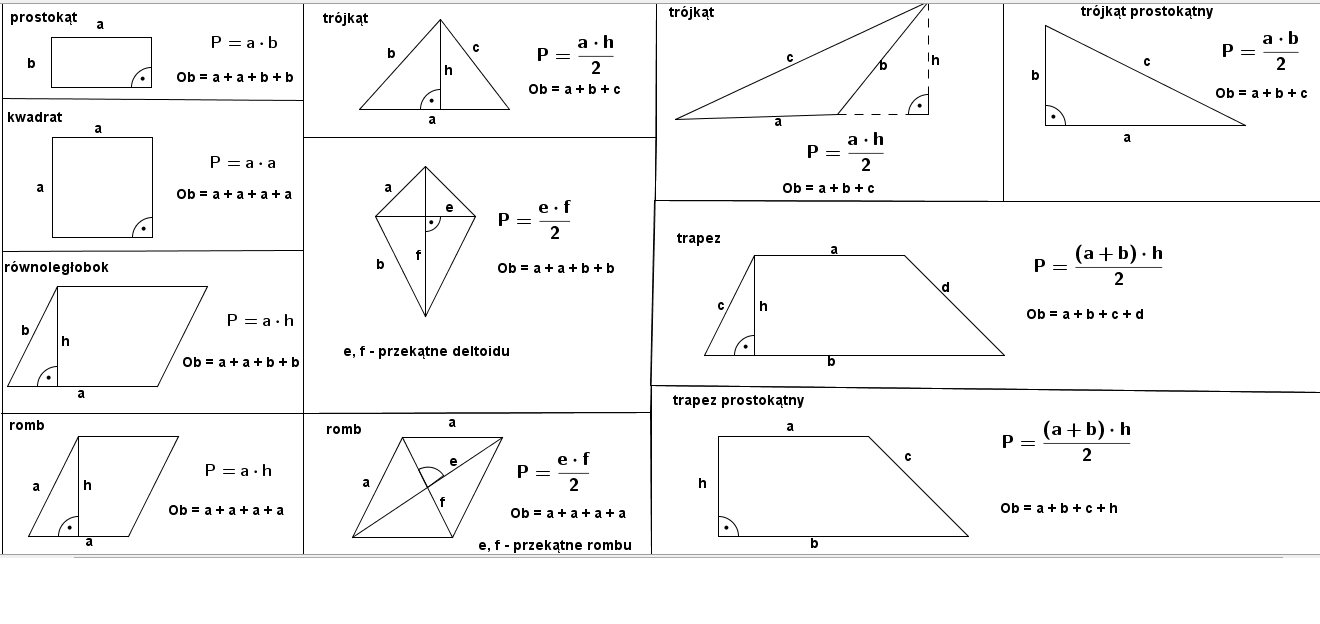
Podstawowe Figury Płaskie i Wzory na Ich Pola

Czas przejść do konkretów. Przedstawię teraz wzory na pola kilku podstawowych figur płaskich. Pamiętaj, że kluczem do sukcesu jest zrozumienie, a nie tylko zapamiętanie wzorów. Zastanów się, dlaczego dany wzór wygląda tak, a nie inaczej. To pomoże Ci go zapamiętać i poprawnie stosować.

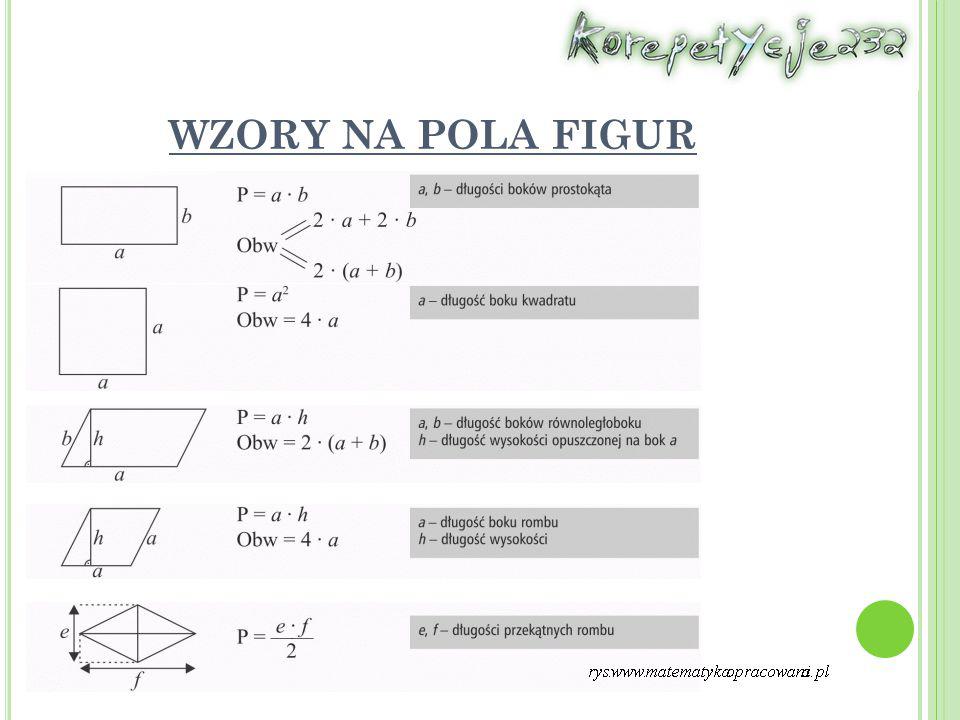
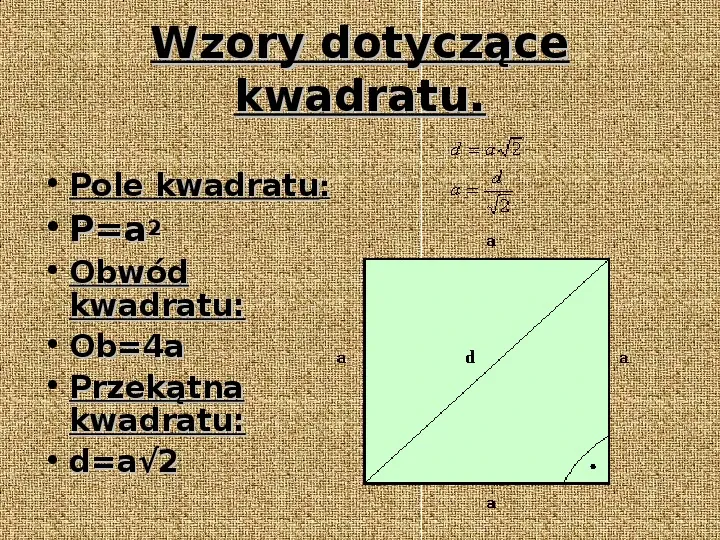
Kwadrat

Kwadrat to czworokąt o wszystkich bokach równych i wszystkich kątach prostych. Jego pole obliczamy bardzo prosto:

P = a²

gdzie a to długość boku kwadratu.

Wyobraź sobie kwadratowy dywan o boku długości 3 metry. Jego pole to 3² = 9 metrów kwadratowych. Proste, prawda?

Prostokąt

Prostokąt to czworokąt o wszystkich kątach prostych. Jego pole obliczamy, mnożąc długość jednego boku przez długość drugiego:

P = a * b

gdzie a i b to długości boków prostokąta.

Pomyśl o prostokątnej ścianie o wymiarach 4 metry na 2.5 metra. Jej pole to 4 * 2.5 = 10 metrów kwadratowych. Potrzebujesz 10 litrów farby, zakładając, że jeden litr wystarcza na pomalowanie jednego metra kwadratowego.

Trójkąt

Obliczanie pola trójkąta jest nieco bardziej złożone, ale nadal stosunkowo proste. Najpopularniejszy wzór to:

P = (a * h) / 2

gdzie a to długość podstawy trójkąta, a h to wysokość opuszczona na tę podstawę.

Wyobraź sobie trójkątny kawałek pizzy. Jeśli jego podstawa ma długość 20 cm, a wysokość opuszczona na tę podstawę wynosi 15 cm, to jego pole wynosi (20 * 15) / 2 = 150 centymetrów kwadratowych.

Istnieją również inne wzory na pole trójkąta, na przykład wzór Herona, który wykorzystuje długości wszystkich trzech boków, ale omówimy go w innym artykule.

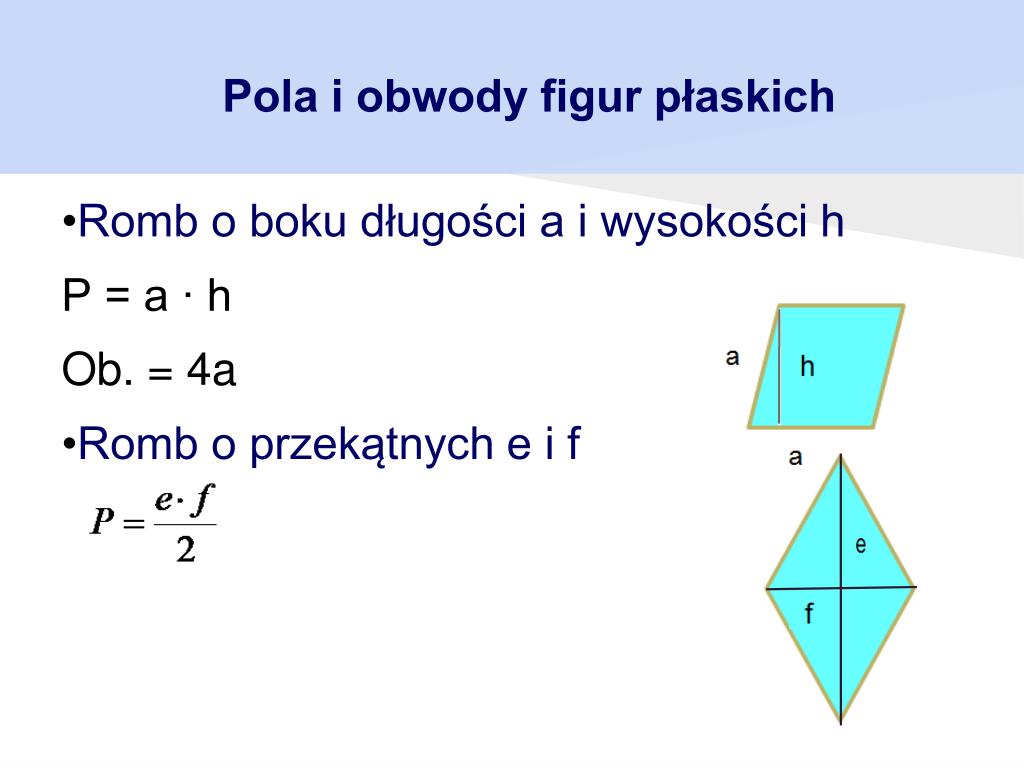
Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Jego pole obliczamy podobnie jak pole prostokąta:

P = a * h

gdzie a to długość podstawy równoległoboku, a h to wysokość opuszczona na tę podstawę.

Zauważ, że wysokość w równoległoboku to odległość między równoległymi bokami, mierzona prostopadle.

Trapez

Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Jego pole obliczamy w następujący sposób:

P = ((a + b) * h) / 2

gdzie a i b to długości podstaw trapezu, a h to wysokość trapezu (odległość między podstawami).

Koło

Koło to figura ograniczona okręgiem. Jego pole obliczamy za pomocą wzoru:

P = π * r²

gdzie π (pi) to stała matematyczna (w przybliżeniu 3.14), a r to promień koła.

Wyobraź sobie okrągły stół o promieniu 1 metra. Jego pole to π * 1² = π, czyli około 3.14 metra kwadratowego.

Czy to naprawdę takie ważne? Adresowanie Contrapunktów

Niektórzy mogą argumentować, że w dzisiejszych czasach, kiedy mamy kalkulatory i aplikacje, znajomość wzorów na pola figur płaskich nie jest już tak istotna. Można po prostu wpisać wartości do kalkulatora i otrzymać wynik. Jest w tym trochę prawdy, ale...

Po pierwsze, zrozumienie wzorów pozwala na lepsze intuicyjne rozumienie geometrii i przestrzeni. Po drugie, znajomość wzorów umożliwia szybkie szacowanie i weryfikowanie wyników obliczeń – unikniemy błędów wynikających z nieprawidłowego wprowadzania danych. Po trzecie, w wielu sytuacjach, szczególnie w warunkach polowych, nie mamy dostępu do kalkulatora czy aplikacji. Znajomość wzorów pozwala na samodzielne rozwiązanie problemu.

Jak Uczyć Się Wzorów?

Najlepszym sposobem na nauczenie się wzorów na pola figur płaskich jest ćwiczenie. Rozwiązuj zadania, rysuj figury, analizuj różne sytuacje. Staraj się zrozumieć, dlaczego dany wzór działa, zamiast bezmyślnie go zapamiętywać. Możesz również:

• Korzystać z interaktywnych narzędzi online i aplikacji, które pozwalają na wizualizację i manipulację figurami geometrycznymi.
• Rysować schematy i notatki, które pomogą Ci zapamiętać wzory i ich zastosowania.
• Uczyć się w grupie, dzielić się wiedzą i wspólnie rozwiązywać zadania.
• Szukać praktycznych przykładów w swoim otoczeniu i próbować obliczać pola różnych powierzchni.

Podsumowanie i Co Dalej?

Znajomość wzorów na pola figur płaskich to nieocenione narzędzie, które przydaje się w wielu aspektach życia. Od planowania remontu, przez projektowanie ogrodu, po rozwiązywanie problemów inżynieryjnych – wszędzie tam, gdzie mamy do czynienia z powierzchniami, wiedza ta okazuje się niezwykle przydatna. Nie zrażaj się, jeśli na początku wydaje Ci się to trudne. Z czasem, dzięki ćwiczeniom i praktyce, wzory staną się dla Ciebie oczywiste i naturalne.

Czy teraz, mając tę wiedzę, spojrzysz na otaczający Cię świat w nieco inny sposób? Czy dostrzegasz więcej geometrycznych kształtów i potencjalnych okazji do wykorzystania wzorów na pola figur płaskich? Spróbuj to sprawdzić w praktyce! Wybierz jakiś przedmiot w swoim otoczeniu i spróbuj oszacować lub dokładnie obliczyć jego powierzchnię. Powodzenia!