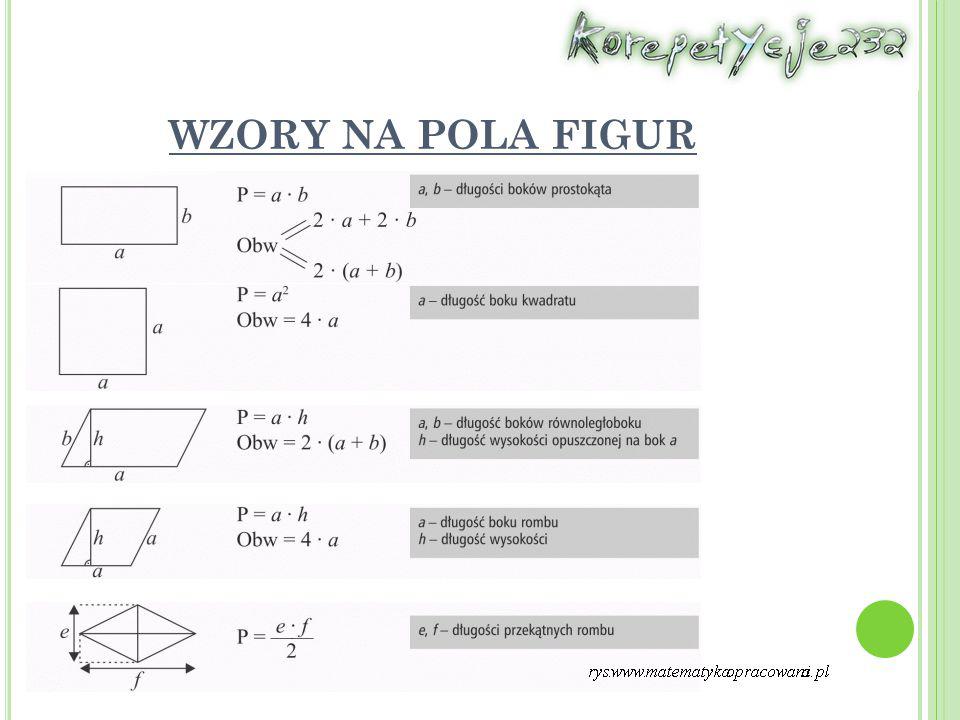
Wzory Na Pola Figur Liceum

Czy pamiętasz ten stres przed klasówką z geometrii w liceum? Wszyscy tam byliśmy. Spędzanie godzin na próbach zapamiętania setek wzorów, z których większość wydawała się kompletnie oderwana od rzeczywistości. Teraz, patrząc wstecz, rozumiemy, że te wzory to klucz do rozwiązywania problemów nie tylko w matematyce, ale i w życiu codziennym. Spróbujmy sobie odświeżyć te wspomnienia, ale w bardziej przystępny i praktyczny sposób.

Dlaczego wzory na pola figur są ważne?

Zanim przejdziemy do konkretnych wzorów, warto zrozumieć, dlaczego w ogóle się nimi zajmujemy. Wyobraź sobie architekta projektującego budynek, inżyniera obliczającego zapotrzebowanie na materiały do budowy mostu, czy nawet krawca wykrawającego ubranie – wszyscy oni, w mniejszym lub większym stopniu, korzystają z wiedzy o polach figur geometrycznych.

Realny wpływ:

• Architektura i budownictwo: Obliczanie powierzchni podłóg, ścian, dachów.
• Inżynieria: Projektowanie maszyn, obliczanie powierzchni skrzydeł samolotów (opór powietrza!).
• Rolnictwo: Określanie powierzchni pól uprawnych, obliczanie zapotrzebowania na nawozy.
• Grafika komputerowa i gry: Tworzenie realistycznych tekstur i modeli 3D.
• Projektowanie wnętrz: Obliczanie ilości farby potrzebnej do pomalowania ścian, dobór dywanów.

Często słyszy się argument, że "nigdy nie będę tego używał/używała". To prawda, że nie każdy potrzebuje znać te wzory na pamięć. Jednak rozumienie podstawowych zasad geometrii uczy logicznego myślenia, rozwiązywania problemów i szacowania, co przydaje się w wielu dziedzinach życia. A poza tym, nigdy nie wiadomo, kiedy ta wiedza okaże się przydatna, np. przy remoncie mieszkania.

Podstawowe figury i ich pola

Zacznijmy od tych, które spotyka się najczęściej. Pamiętaj, że kluczem jest zrozumienie, dlaczego dany wzór wygląda tak, a nie inaczej. Spróbujmy podejść do tego intuicyjnie.

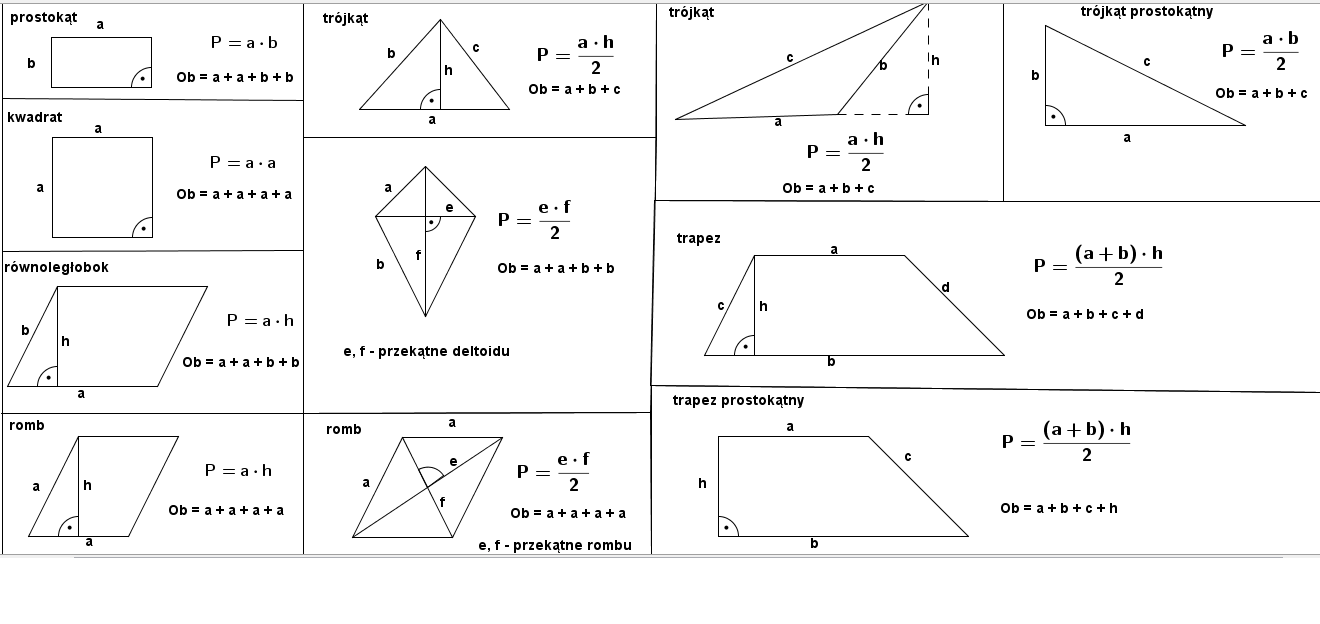
Kwadrat

Wzór: P = a², gdzie 'a' to długość boku.

Wyjaśnienie: Kwadrat to po prostu prostokąt, który ma wszystkie boki równe. Zatem pole to po prostu bok razy bok.

Prostokąt

Wzór: P = a * b, gdzie 'a' i 'b' to długości boków.

Wyjaśnienie: Intuicyjnie, możemy sobie wyobrazić, że prostokąt to wiele identycznych odcinków o długości 'a', ułożonych obok siebie na długości 'b'.

Trójkąt

Wzór: P = (a * h) / 2, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.

Wyjaśnienie: Wyobraź sobie prostokąt o podstawie 'a' i wysokości 'h'. Trójkąt o tej samej podstawie i wysokości zajmuje dokładnie połowę jego powierzchni. Dlatego dzielimy wynik przez 2.

• Trójkąt równoboczny: P = (a² * √3) / 4. Wynika to z zastosowania twierdzenia Pitagorasa do obliczenia wysokości.
• Wzór Herona: P = √[s(s-a)(s-b)(s-c)], gdzie s = (a+b+c)/2 (połowa obwodu). Przydatny, gdy znamy tylko długości boków.

Równoległobok

Wzór: P = a * h, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.

Wyjaśnienie: Możemy przekształcić równoległobok w prostokąt, "odcinając" trójkąt z jednej strony i "doklejając" go z drugiej. Wysokość pozostaje taka sama, a podstawa się nie zmienia.

Romb

Wzór 1: P = a * h, gdzie 'a' to długość boku, a 'h' to wysokość opuszczona na ten bok (jak w równoległoboku).

Wzór 2: P = (d1 * d2) / 2, gdzie 'd1' i 'd2' to długości przekątnych.

Wyjaśnienie: Romb to specjalny przypadek równoległoboku, w którym wszystkie boki są równe. Drugi wzór wynika z tego, że romb można podzielić na cztery przystające trójkąty prostokątne, których pole łatwo obliczyć znając przekątne.

Trapez

Wzór: P = ((a + b) * h) / 2, gdzie 'a' i 'b' to długości podstaw, a 'h' to wysokość.

Wyjaśnienie: Możemy sobie wyobrazić, że trapez to "ścięty" trójkąt. Możemy też traktować go jako średnią arytmetyczną długości podstaw pomnożoną przez wysokość.

Koło

Wzór: P = π * r², gdzie 'r' to promień koła, a π (pi) to stała matematyczna w przybliżeniu równa 3.14159.

Wyjaśnienie: To już trochę trudniejsze do intuicyjnego wytłumaczenia. Można spróbować podzielić koło na bardzo małe wycinki, które przypominają trójkąty. Sumując ich pola, otrzymamy wzór na pole koła. π (pi) jest fundamentalną stałą, która pojawia się wszędzie tam, gdzie mamy do czynienia z okręgami i kulami.

Figury złożone

Co zrobić, gdy mamy do czynienia z figurą, która nie jest jedną z wyżej wymienionych? Kluczem jest rozłożenie figury na prostsze kształty, których pola potrafimy obliczyć. Następnie sumujemy (lub odejmujemy, jeśli trzeba) pola tych mniejszych figur.

Przykład: Figura składająca się z prostokąta i półkola. Obliczamy pole prostokąta, pole koła (z którego bierzemy połowę) i sumujemy te wartości.

Przykładowe zadania

Zadanie 1: Pokój ma wymiary 4m x 5m. Ile metrów kwadratowych parkietu potrzeba do wyłożenia podłogi?

Rozwiązanie: Pole podłogi to 4m * 5m = 20m². Potrzeba 20 metrów kwadratowych parkietu.

Zadanie 2: Ogródek ma kształt trapezu o podstawach 8m i 12m oraz wysokości 5m. Jakie jest pole tego ogródka?

Rozwiązanie: Pole ogródka to ((8m + 12m) * 5m) / 2 = 50m².

Zadanie 3: Oblicz pole koła o promieniu 3cm.

Rozwiązanie: Pole koła to π * (3cm)² ≈ 3.14159 * 9cm² ≈ 28.27 cm².

Dodatkowe wskazówki

• Rysuj! Zawsze warto narysować sobie figurę, nawet jeśli zadanie tego nie wymaga. Pomaga to zwizualizować problem i uniknąć błędów.
• Zwracaj uwagę na jednostki! Pamiętaj o zamianie jednostek, jeśli są różne (np. centymetry na metry). Wynik zawsze podawaj w odpowiedniej jednostce (np. metry kwadratowe).
• Używaj kalkulatora! Szczególnie przy obliczeniach z liczbą π lub pierwiastkami.
• Ćwicz! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz wzory i zasady geometrii.

Pamiętaj: Nie chodzi o to, żeby ślepo zapamiętywać wzory, ale żeby je rozumieć i umieć zastosować w praktyce. Traktuj to jako wyzwanie intelektualne, a nie jako przykry obowiązek. Zrozumienie wzorów na pola figur to inwestycja w Twoją przyszłość, która może się przydać w wielu niespodziewanych sytuacjach.

Jakie zastosowanie wzorów na pola figur geometrycznych wydaje Ci się najbardziej interesujące i dlaczego?