Wzory Na Pola Figur Klasa 8

Obliczenie pola powierzchni jest kluczową umiejętnością w matematyce, szczególnie w geometrii. W klasie 8. uczniowie zapoznają się z wzorami na pola różnych figur płaskich. Zrozumienie tych wzorów i umiejętność ich stosowania jest niezbędne do rozwiązywania zadań geometrycznych, ale również przydatne w życiu codziennym.

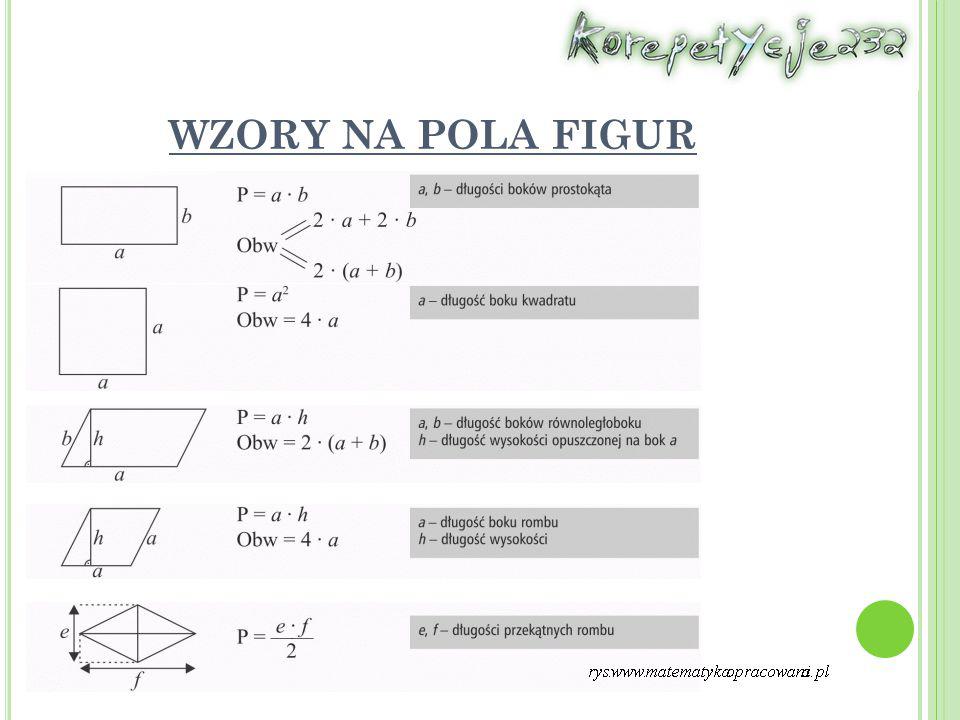
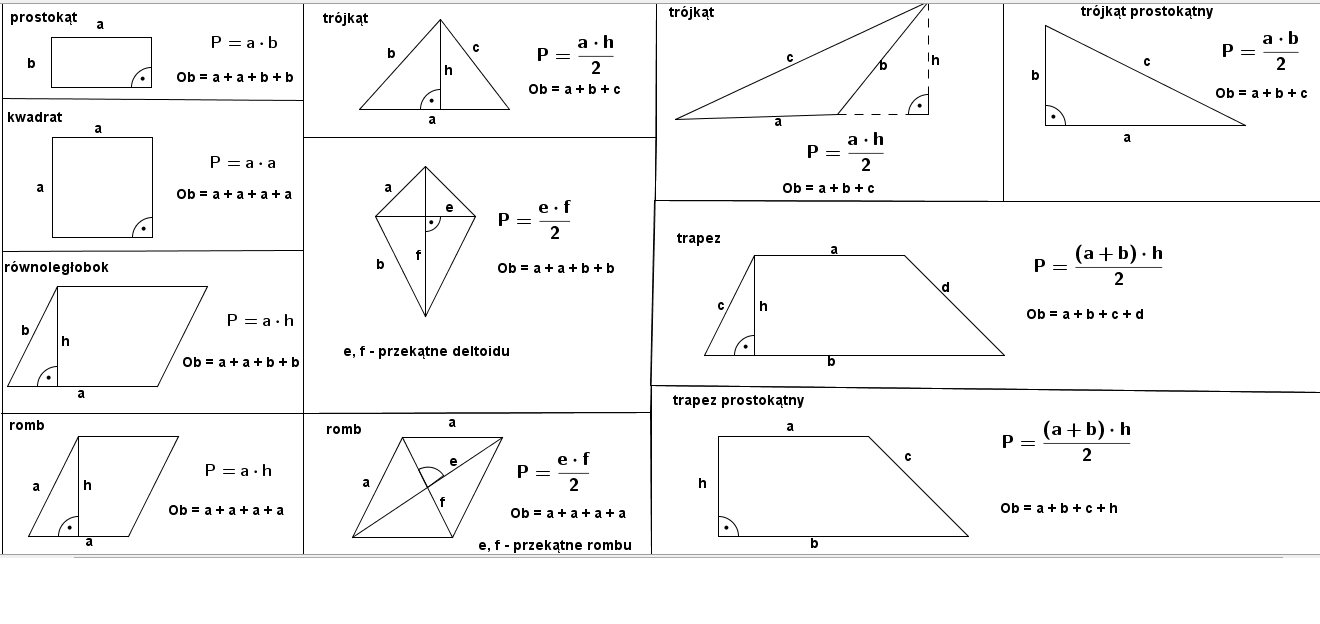
Wzory na Pola Podstawowych Figur

W klasie 8 omawia się przede wszystkim wzory na pola następujących figur:

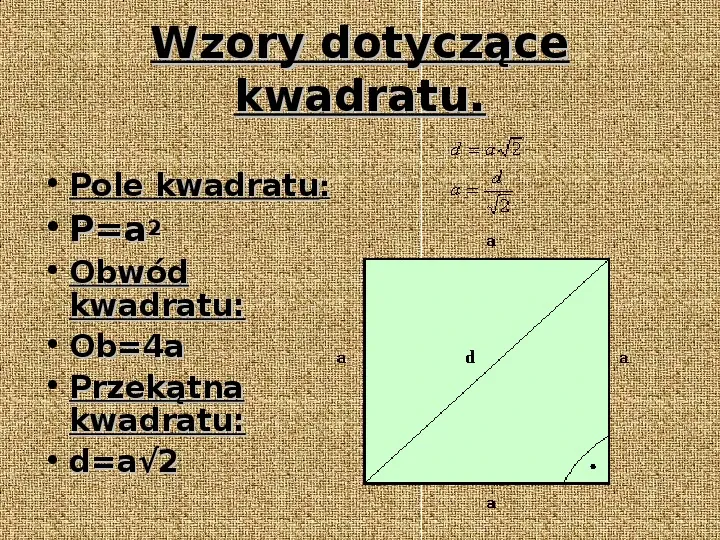
Kwadrat

Kwadrat to czworokąt, który ma wszystkie boki równe i wszystkie kąty proste. Jego pole obliczamy bardzo prosto, mnożąc długość boku przez samą siebie:

P = a * a = a²

Gdzie a to długość boku kwadratu.

Przykład: Kwadrat ma bok długości 5 cm. Jego pole wynosi P = 5 cm * 5 cm = 25 cm².

Prostokąt

Prostokąt to czworokąt, który ma wszystkie kąty proste. Jego pole obliczamy, mnożąc długość jednego boku (długość) przez długość drugiego boku (szerokość):

P = a * b

Gdzie a to długość, a b to szerokość prostokąta.

Przykład: Prostokąt ma długość 8 cm i szerokość 3 cm. Jego pole wynosi P = 8 cm * 3 cm = 24 cm².

Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Jego pole obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę:

P = a * h

Gdzie a to długość podstawy, a h to wysokość.

Przykład: Równoległobok ma podstawę długości 10 cm, a wysokość opuszczona na tę podstawę wynosi 4 cm. Jego pole wynosi P = 10 cm * 4 cm = 40 cm².

Romb

Romb to równoległobok, który ma wszystkie boki równe. Pole rombu możemy obliczyć na dwa sposoby: tak jak pole równoległoboku (podstawa razy wysokość) lub korzystając z długości jego przekątnych:

P = a * h lub P = (d₁ * d₂) / 2

Gdzie a to długość boku, h to wysokość, a d₁ i d₂ to długości przekątnych.

Przykład 1: Romb ma bok długości 6 cm, a wysokość wynosi 5 cm. Jego pole wynosi P = 6 cm * 5 cm = 30 cm².

Przykład 2: Romb ma przekątne o długościach 8 cm i 6 cm. Jego pole wynosi P = (8 cm * 6 cm) / 2 = 24 cm².

Trójkąt

Trójkąt to figura, która ma trzy boki. Jego pole obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę, a następnie dzieląc wynik przez 2:

P = (a * h) / 2

Gdzie a to długość podstawy, a h to wysokość.

Przykład: Trójkąt ma podstawę długości 7 cm, a wysokość opuszczona na tę podstawę wynosi 4 cm. Jego pole wynosi P = (7 cm * 4 cm) / 2 = 14 cm².

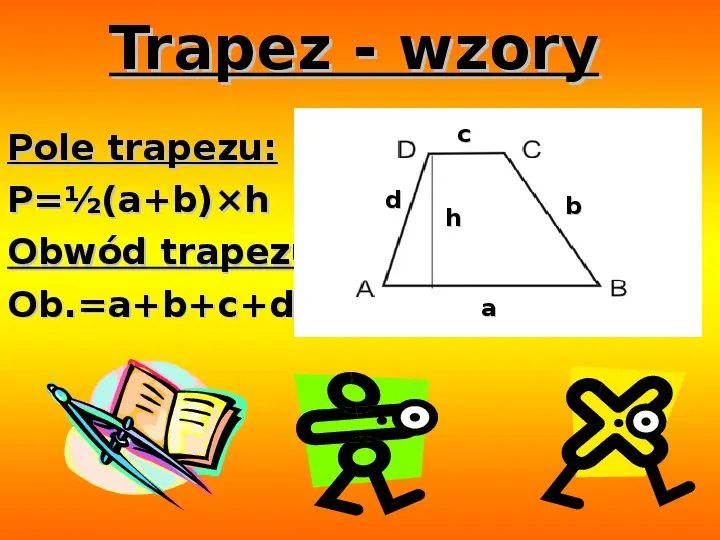
Trapez

Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych (zwanych podstawami). Jego pole obliczamy, dodając do siebie długości podstaw, mnożąc wynik przez wysokość, a następnie dzieląc całość przez 2:

P = ((a + b) * h) / 2

Gdzie a i b to długości podstaw trapezu, a h to wysokość.

Przykład: Trapez ma podstawy o długościach 5 cm i 9 cm, a wysokość wynosi 3 cm. Jego pole wynosi P = ((5 cm + 9 cm) * 3 cm) / 2 = 21 cm².

Koło

Koło to zbiór wszystkich punktów na płaszczyźnie, które znajdują się w odległości nie większej niż promień od danego punktu (środka koła). Jego pole obliczamy, używając liczby Pi (π), która w przybliżeniu wynosi 3,14:

P = π * r²

Gdzie r to promień koła.

Przykład: Koło ma promień długości 4 cm. Jego pole wynosi P = π * (4 cm)² ≈ 3,14 * 16 cm² ≈ 50,24 cm².

Zastosowanie Wzorów w Życiu Codziennym

Wzory na pola figur znajdują szerokie zastosowanie w życiu codziennym. Przykłady obejmują:

Budownictwo: Obliczanie ilości materiałów potrzebnych do pokrycia podłogi, ścian, dachu (np. płytek, paneli, farby).
Ogrodnictwo: Obliczanie powierzchni trawnika, rabat kwiatowych, aby zaplanować nasadzenia i zakupić odpowiednią ilość nasion lub sadzonek.
Projektowanie wnętrz: Obliczanie powierzchni ścian przy doborze tapet lub farb, dobór dywanów o odpowiedniej wielkości.
Krawiectwo: Obliczanie ilości materiału potrzebnego do uszycia ubrania, uwzględniając kroje i wzory.
Geodezja i kartografia: Obliczanie powierzchni działek, terenów, państw na mapach.

Przykład: Chcesz pomalować pokój. Ściany mają kształt prostokątów o wymiarach 3m x 2.5m (dwie ściany) i 4m x 2.5m (dwie ściany). Łączna powierzchnia ścian to 2 * (3m * 2.5m) + 2 * (4m * 2.5m) = 15 m² + 20 m² = 35 m². Jeżeli puszka farby wystarcza na pomalowanie 10 m², potrzebujesz 35 m² / 10 m²/puszkę = 3.5 puszki. Zatem musisz kupić 4 puszki farby.

Praktyczne Wskazówki

Aby skutecznie stosować wzory na pola figur, warto pamiętać o kilku ważnych rzeczach:

Jednostki miary: Upewnij się, że wszystkie wymiary są podane w tej samej jednostce (np. centymetry, metry). Jeśli nie są, zamień je na tę samą jednostkę przed rozpoczęciem obliczeń.
Rysunek: Zawsze warto narysować sobie figurę, aby lepiej zrozumieć zadanie i oznaczyć odpowiednie wymiary.
Wybór wzoru: Upewnij się, że używasz odpowiedniego wzoru dla danej figury.
Sprawdzanie wyniku: Po obliczeniu pola sprawdź, czy wynik jest sensowny. Na przykład, pole prostokąta nie może być mniejsze od długości jego krótszego boku.
Zapamiętywanie wzorów: Regularne powtarzanie wzorów pomaga w ich zapamiętaniu. Można tworzyć własne mnemotechniki lub korzystać z gotowych.

Zadania Treningowe

Regularne rozwiązywanie zadań to najlepszy sposób na utrwalenie wiedzy i nabycie wprawy w stosowaniu wzorów na pola figur. Można korzystać z podręczników, zbiorów zadań, arkuszy ćwiczeń online.

Przykładowe zadanie: Oblicz pole trapezu równoramiennego, którego podstawy mają długości 6 cm i 10 cm, a ramię ma długość 5 cm. Wysokość trapezu wynosi 4 cm.

Rozwiązanie: P = ((6 cm + 10 cm) * 4 cm) / 2 = 32 cm²

Podsumowanie

Znajomość wzorów na pola figur to niezbędny element edukacji matematycznej w klasie 8. Umiejętność ich stosowania jest kluczowa nie tylko do rozwiązywania zadań geometrycznych, ale również przydatna w wielu sytuacjach życiowych. Regularne ćwiczenia i praktyczne zastosowanie wiedzy pomogą w utrwaleniu wzorów i zwiększą pewność siebie w rozwiązywaniu problemów.

Zatem, weź kartkę, długopis i zacznij ćwiczyć! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te wzory i łatwiej będziesz mógł/mogła je stosować. Pamiętaj, praktyka czyni mistrza!