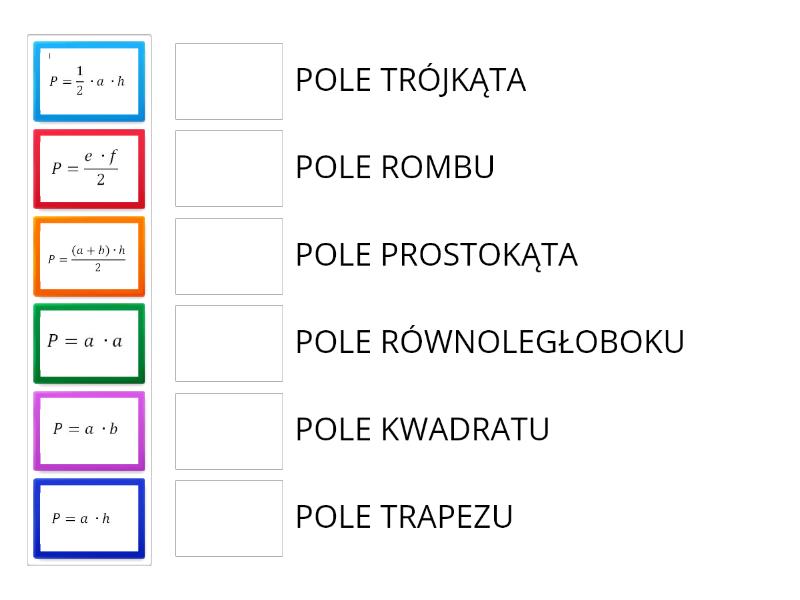
Wzory Na Pola Figur Klasa 7

Masz problem z obliczaniem pól figur geometrycznych? Bez obaw! Ten artykuł jest dla Ciebie, uczniu klasy 7, który chce raz na zawsze opanować te zagadnienia. Postaramy się wyjaśnić wszystko krok po kroku, w przystępny sposób, wykorzystując praktyczne przykłady i wizualizacje. Koniec z nudnymi wzorami! Czas na praktyczną wiedzę, którą wykorzystasz na sprawdzianach i w życiu codziennym!

Dlaczego Wzory Na Pola Figur Są Ważne?

Zastanawiasz się, po co w ogóle uczyć się tych wszystkich wzorów? Odpowiedź jest prosta: pola figur geometrycznych otaczają nas wszędzie! Obliczanie powierzchni podłogi przy remoncie, szacowanie ilości farby potrzebnej do pomalowania ściany, a nawet obliczanie powierzchni pizzy – to wszystko wymaga znajomości tych podstawowych wzorów. Zrozumienie geometrii pomoże Ci również w innych dziedzinach, takich jak architektura, inżynieria i grafika komputerowa.

Co więcej, opanowanie tych umiejętności buduje logiczne myślenie i zdolność rozwiązywania problemów. To inwestycja w Twoją przyszłość!

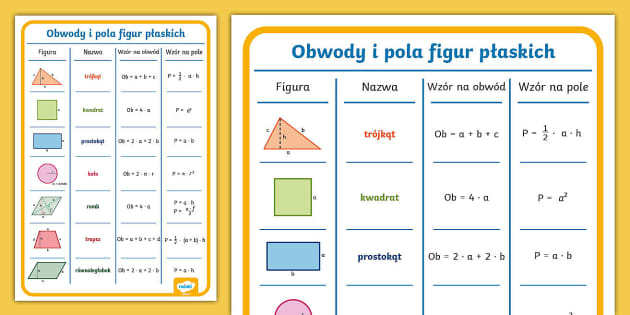
Podstawowe Figury i Ich Wzory

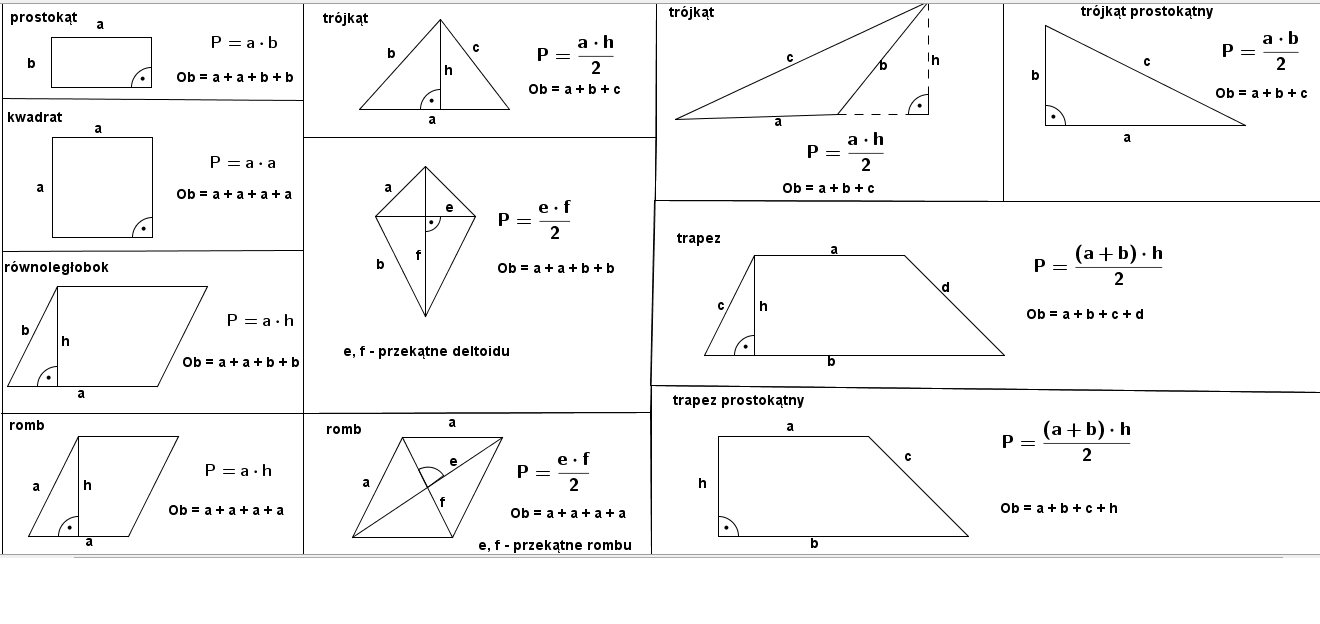
Zaczynamy od podstawowych figur geometrycznych, które spotkasz najczęściej. Przygotuj się na krótką, ale treściwą powtórkę:

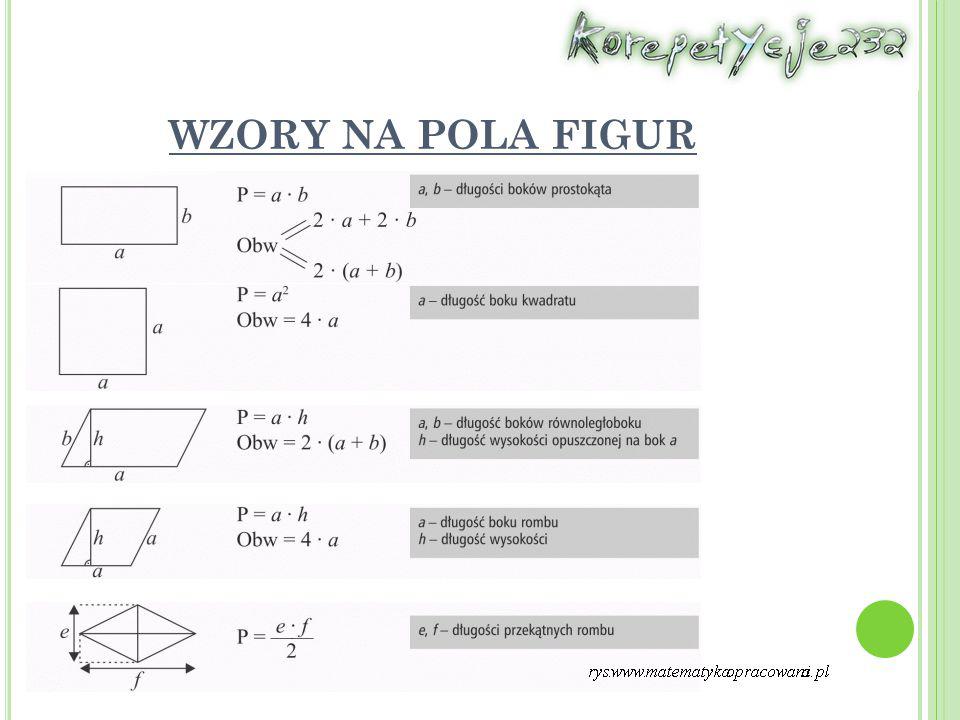
Prostokąt

Prostokąt to figura, która ma dwa boki o równej długości. Oznaczmy długość jednego boku jako a, a drugiego jako b. Wtedy wzór na pole prostokąta wygląda następująco:

Pole prostokąta (P) = a * b

Przykład: Jeśli bok prostokąta ma długość 5 cm, a drugi bok 8 cm, to jego pole wynosi P = 5 cm * 8 cm = 40 cm². Pamiętaj o jednostkach! Pole zawsze wyrażamy w jednostkach kwadratowych.

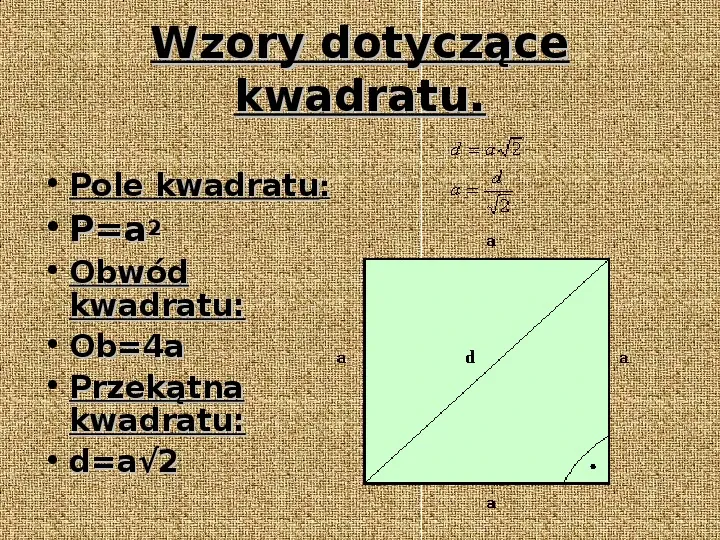
Kwadrat

Kwadrat to szczególny przypadek prostokąta, w którym wszystkie boki są równe. Oznaczmy długość boku kwadratu jako a. Wtedy wzór na pole kwadratu wygląda następująco:

Pole kwadratu (P) = a * a = a²

Przykład: Jeśli bok kwadratu ma długość 6 cm, to jego pole wynosi P = 6 cm * 6 cm = 36 cm².

Równoległobok

Równoległobok to figura, która ma dwie pary boków równoległych. Oznaczmy długość podstawy jako a, a wysokość (odległość między podstawami) jako h. Wtedy wzór na pole równoległoboku wygląda następująco:

Pole równoległoboku (P) = a * h

Przykład: Jeśli podstawa równoległoboku ma długość 10 cm, a wysokość wynosi 4 cm, to jego pole wynosi P = 10 cm * 4 cm = 40 cm².

Romb

Romb to równoległobok, który ma wszystkie boki równe. Możemy obliczyć jego pole na dwa sposoby: tak jak równoległobok (podstawa razy wysokość) lub za pomocą przekątnych. Oznaczmy długość jednej przekątnej jako d1, a drugiej jako d2. Wtedy wzór na pole rombu z wykorzystaniem przekątnych wygląda następująco:

Pole rombu (P) = (d1 * d2) / 2

Przykład: Jeśli jedna przekątna rombu ma długość 8 cm, a druga 6 cm, to jego pole wynosi P = (8 cm * 6 cm) / 2 = 24 cm².

Trójkąt

Trójkąt to figura o trzech bokach. Oznaczmy długość podstawy jako a, a wysokość (odległość od wierzchołka do podstawy) jako h. Wtedy wzór na pole trójkąta wygląda następująco:

Pole trójkąta (P) = (a * h) / 2

Przykład: Jeśli podstawa trójkąta ma długość 7 cm, a wysokość wynosi 5 cm, to jego pole wynosi P = (7 cm * 5 cm) / 2 = 17.5 cm².

Warto pamiętać, że wysokość musi być prostopadła do podstawy. Czasami będziesz musiał ją dorysować, żeby móc obliczyć pole.

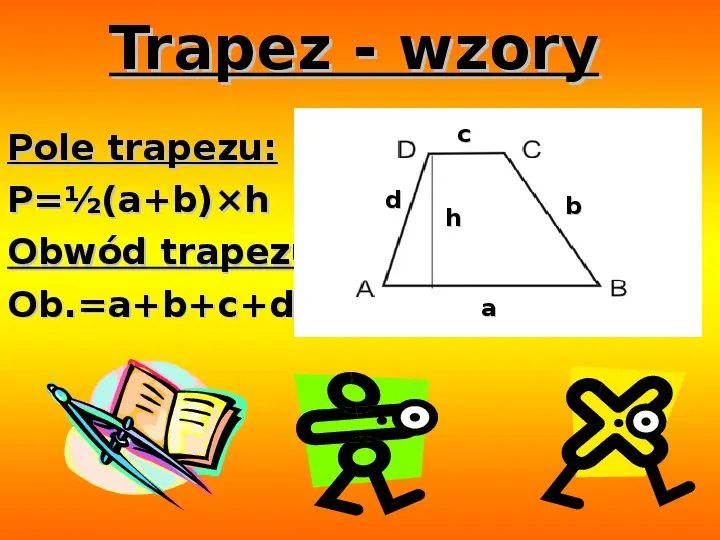
Trapez

Trapez to figura, która ma przynajmniej jedną parę boków równoległych (nazywamy je podstawami). Oznaczmy długość jednej podstawy jako a, długość drugiej podstawy jako b, a wysokość (odległość między podstawami) jako h. Wtedy wzór na pole trapezu wygląda następująco:

Pole trapezu (P) = ((a + b) * h) / 2

Przykład: Jeśli jedna podstawa trapezu ma długość 9 cm, druga 5 cm, a wysokość wynosi 3 cm, to jego pole wynosi P = ((9 cm + 5 cm) * 3 cm) / 2 = 21 cm².

Koło

Koło to figura, której wszystkie punkty są w równej odległości od środka. Tę odległość nazywamy promieniem (r). Wzór na pole koła wygląda następująco:

Pole koła (P) = π * r²

Gdzie π (pi) to stała matematyczna, w przybliżeniu równa 3.14.

Przykład: Jeśli promień koła ma długość 4 cm, to jego pole wynosi P = 3.14 * (4 cm)² = 3.14 * 16 cm² = 50.24 cm².

Praktyczne Wskazówki i Triki

Zawsze rysuj figurę! Nawet jeśli zadanie tego nie wymaga. Rysunek pomoże Ci zrozumieć zadanie i zidentyfikować potrzebne dane.
Zapisuj wzory! Powtarzanie wzorów utrwala je w pamięci. Możesz stworzyć sobie kartkę ze wszystkimi wzorami i mieć ją zawsze pod ręką.
Pamiętaj o jednostkach! Pole zawsze wyrażamy w jednostkach kwadratowych (cm², m², km² itd.).
Przekształcaj wzory! Czasami będziesz musiał przekształcić wzór, żeby obliczyć np. wysokość, znając pole i podstawę.
Dziel figury na prostsze! Jeśli masz do czynienia ze skomplikowaną figurą, spróbuj podzielić ją na prostsze figury (np. prostokąty i trójkąty), obliczyć ich pola oddzielnie, a następnie dodać.
Korzystaj z zasobów online! W Internecie znajdziesz mnóstwo interaktywnych narzędzi i kalkulatorów, które pomogą Ci obliczyć pole różnych figur.

Przykładowe Zadania z Rozwiązaniami

Teraz czas na praktykę! Rozwiążmy kilka przykładowych zadań:

Zadanie 1: Oblicz pole prostokąta o bokach długości 7 cm i 12 cm.

Rozwiązanie:

P = a * b = 7 cm * 12 cm = 84 cm²

Zadanie 2: Oblicz pole trójkąta o podstawie 8 cm i wysokości 6 cm.

Rozwiązanie:

P = (a * h) / 2 = (8 cm * 6 cm) / 2 = 24 cm²

Zadanie 3: Oblicz pole koła o promieniu 5 cm (π ≈ 3.14).

Rozwiązanie:

P = π * r² = 3.14 * (5 cm)² = 3.14 * 25 cm² = 78.5 cm²

Zadanie 4: Oblicz pole rombu o przekątnych długości 10 cm i 4 cm.

Rozwiązanie:

P = (d1 * d2) / 2 = (10 cm * 4 cm) / 2 = 20 cm²

Gdzie Szukać Więcej Pomocy?

Jeśli czujesz, że potrzebujesz więcej pomocy, skorzystaj z następujących zasobów:

Podręcznik do matematyki: Tam znajdziesz szczegółowe wyjaśnienia i przykłady.
Zeszyt ćwiczeń: Rozwiązuj zadania, żeby utrwalić wiedzę.
Nauczyciel matematyki: Nie bój się zadawać pytań! Nauczyciel jest po to, żeby Ci pomóc.
Korepetycje: Jeśli potrzebujesz indywidualnej pomocy, rozważ korepetycje z matematyki.
Internet: W Internecie znajdziesz mnóstwo stron internetowych, filmów i interaktywnych ćwiczeń. Szukaj stron z jasnymi przykładami i rozwiązanymi zadaniami.

Podsumowanie i Wartość

Gratulacje! Dotarłeś do końca tego artykułu. Opanowanie wzorów na pola figur geometrycznych to ważny krok w Twojej edukacji. Pamiętaj, że praktyka czyni mistrza. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te zagadnienia.

Dzięki temu artykułowi: