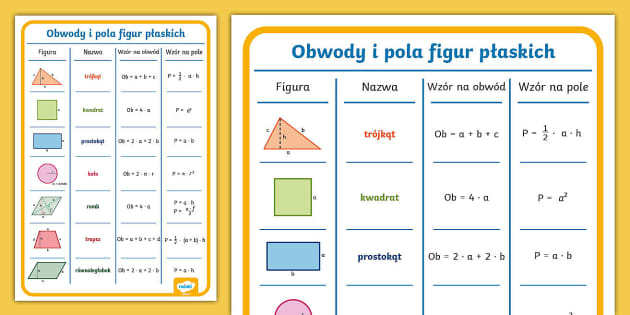
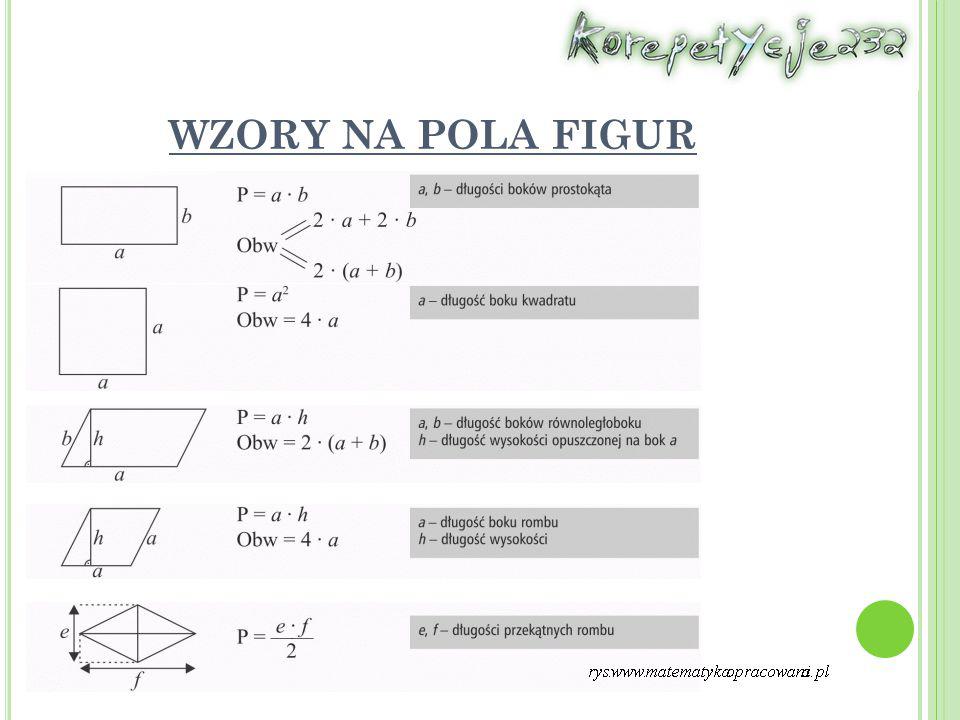
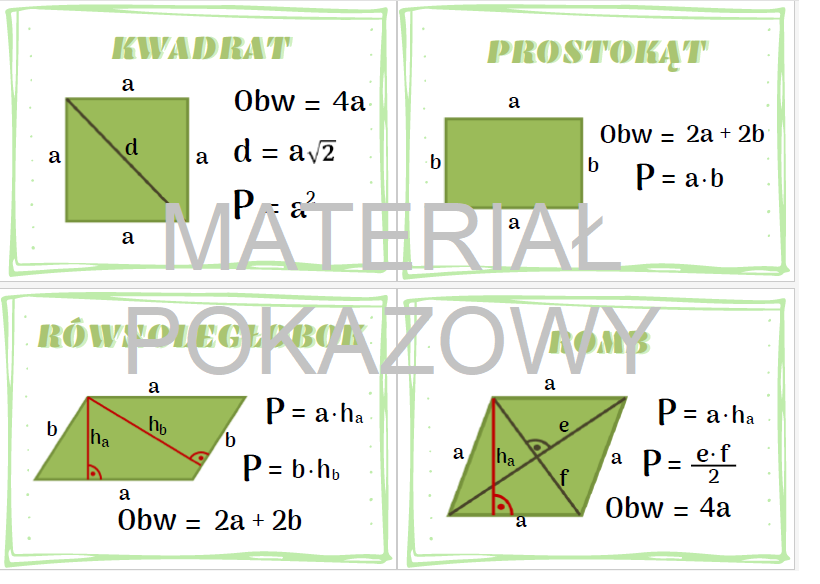
Wzory Na Pola Figur Klasa 6

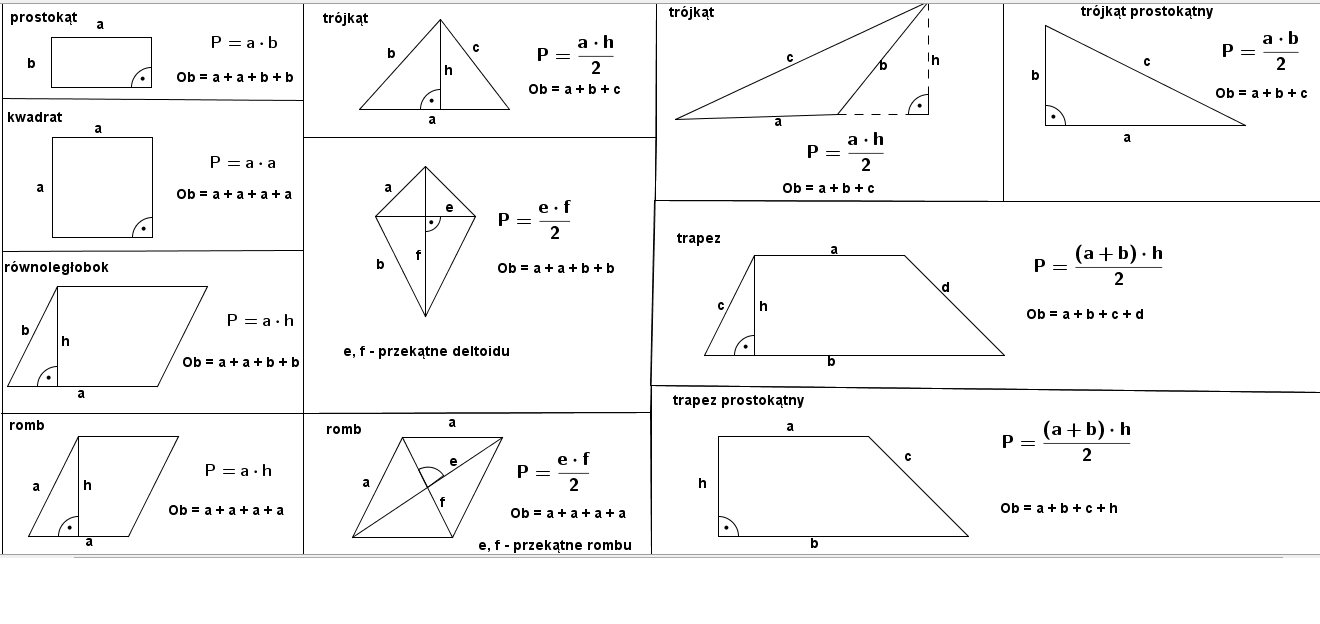
Czy kiedykolwiek zastanawiałeś się, jak obliczyć, ile farby potrzebujesz do pomalowania pokoju? A może jak podzielić pizzę sprawiedliwie między przyjaciółmi? Odpowiedź często leży w znajomości wzorów na pola figur geometrycznych. Dla ucznia klasy 6, to fundament, który otwiera drzwi do bardziej zaawansowanej matematyki i zastosowań w życiu codziennym.

Wiem, że na początku wzory mogą wydawać się skomplikowane i trudne do zapamiętania. Ale spokojnie, postaram się wytłumaczyć je w prosty i przystępny sposób, tak abyś zrozumiał, skąd się biorą i jak je stosować. Razem pokonamy tę przeszkodę!

Podstawowe Figury i Wzory na Pola

Zacznijmy od figur, które prawdopodobnie już znasz. Pamiętaj, że pole figury to miara powierzchni, jaką ta figura zajmuje. Wyrażamy ją w jednostkach kwadratowych, np. centymetrach kwadratowych (cm²) lub metrach kwadratowych (m²).

Kwadrat

Kwadrat to figura, która ma cztery równe boki i cztery kąty proste. Wyobraź sobie, że masz płytkę chodnikową w kształcie kwadratu. Jak obliczyć jej powierzchnię?

Wzór na pole kwadratu jest bardzo prosty:

P = a * a = a²

Gdzie P oznacza pole kwadratu, a a to długość boku.

Przykład: Jeśli bok kwadratu ma długość 5 cm, to jego pole wynosi 5 cm * 5 cm = 25 cm².

Prostokąt

Prostokąt, podobnie jak kwadrat, ma cztery kąty proste, ale jego boki nie muszą być równe. Ma dwie pary boków równych i równoległych. Pomyśl o kartce papieru – to typowy prostokąt.

Wzór na pole prostokąta:

P = a * b

Gdzie P oznacza pole prostokąta, a to długość jednego boku, a b to długość drugiego boku.

Przykład: Jeśli prostokąt ma boki o długości 8 cm i 3 cm, to jego pole wynosi 8 cm * 3 cm = 24 cm².

Trójkąt

Trójkąt to figura o trzech bokach i trzech kątach. Wyróżniamy różne rodzaje trójkątów: równoboczny, równoramienny, prostokątny, ostrokątny i rozwartokątny. Ale wzór na pole trójkąta jest uniwersalny.

Wzór na pole trójkąta:

P = (a * h) / 2

Gdzie P oznacza pole trójkąta, a to długość podstawy, a h to wysokość opuszczona na tę podstawę (odcinek prostopadły do podstawy, łączący ją z wierzchołkiem trójkąta).

Przykład: Jeśli podstawa trójkąta ma długość 10 cm, a wysokość opuszczona na tę podstawę ma długość 6 cm, to jego pole wynosi (10 cm * 6 cm) / 2 = 30 cm².

Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równych i równoległych. W przeciwieństwie do prostokąta, kąty równoległoboku nie muszą być proste. Wyobraź sobie lekko przechylony prostokąt.

Wzór na pole równoległoboku:

P = a * h

Gdzie P oznacza pole równoległoboku, a to długość podstawy, a h to wysokość opuszczona na tę podstawę (odcinek prostopadły do podstawy, łączący ją z przeciwległym bokiem).

Przykład: Jeśli podstawa równoległoboku ma długość 7 cm, a wysokość opuszczona na tę podstawę ma długość 4 cm, to jego pole wynosi 7 cm * 4 cm = 28 cm².

Romb

Romb to równoległobok, który ma wszystkie boki równe. Możemy myśleć o nim jako o "przechylonym kwadracie".

Romb ma dwa sposoby obliczania pola:

Używając podstawy i wysokości: P = a * h (tak jak w równoległoboku)
Używając długości przekątnych: P = (e * f) / 2, gdzie e i f to długości przekątnych rombu.

Przykład: Jeśli romb ma bok o długości 6 cm, wysokość opuszczoną na ten bok o długości 5 cm, to jego pole wynosi 6 cm * 5 cm = 30 cm². Jeśli przekątne rombu mają długości 8 cm i 4 cm, to jego pole wynosi (8 cm * 4 cm) / 2 = 16 cm².

Trapez

Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Te boki równoległe nazywamy podstawami trapezu (a i b), a odległość między nimi to wysokość trapezu (h).

Wzór na pole trapezu:

P = ((a + b) * h) / 2

Gdzie P oznacza pole trapezu, a i b to długości podstaw, a h to wysokość.

Przykład: Jeśli podstawy trapezu mają długości 9 cm i 5 cm, a wysokość ma długość 3 cm, to jego pole wynosi ((9 cm + 5 cm) * 3 cm) / 2 = 21 cm².

Praktyczne Zastosowania Wzorów na Pola

Wzory na pola figur geometrycznych są niezwykle przydatne w życiu codziennym. Oto kilka przykładów:

Planowanie remontu: Obliczanie, ile płytek ceramicznych potrzebujesz do wyłożenia podłogi w łazience (prostokąt).
Projektowanie ogrodu: Obliczanie, ile trawy potrzebujesz do obsiania trawnika (trójkąt, prostokąt, kwadrat).
Gotowanie: Obliczanie, jak dużą blachę do pieczenia potrzebujesz na ciasto.
Szycie: Obliczanie, ile materiału potrzebujesz na uszycie spódnicy (trapez, trójkąt).
Budownictwo: Obliczanie, ile materiałów budowlanych potrzebujesz na budowę domu (ściany, dach).

Wskazówki dotyczące Nauki Wzorów

Zapamiętywanie wzorów na pola figur geometrycznych może być łatwiejsze, jeśli zastosujesz kilka prostych trików:

Zrozumienie, a nie wkuwanie: Staraj się zrozumieć, skąd biorą się wzory. Wizualizuj sobie figury i wyobraź sobie, jak dzielisz je na mniejsze kwadraty, aby obliczyć ich pole.
Rysowanie: Rysuj figury i oznaczaj ich boki i wysokości. To pomoże Ci lepiej zapamiętać wzory.
Przykłady: Rozwiązuj dużo zadań z przykładami. Im więcej ćwiczysz, tym lepiej zapamiętasz wzory.
Skróty i mnemotechniki: Twórz własne skróty i rymowanki, które pomogą Ci zapamiętać wzory. Na przykład, możesz zapamiętać wzór na pole trójkąta jako "podstawa razy wysokość przez dwa".
Używaj aplikacji i gier: Istnieje wiele aplikacji i gier, które pomogą Ci w nauce wzorów na pola figur geometrycznych.

Pamiętaj!

Nauka wzorów na pola figur geometrycznych to inwestycja w przyszłość. Dzięki tej wiedzy będziesz mógł rozwiązywać problemy matematyczne, które napotkasz w szkole i w życiu codziennym. Nie zniechęcaj się, jeśli na początku będzie trudno. Ćwicz regularnie, a zobaczysz, że z czasem wszystko stanie się prostsze i bardziej zrozumiałe.

Życzę Ci powodzenia w nauce!