Wzory Na Pola Figur Klasa 5

Czy kiedykolwiek zastanawiałeś się, jak zmierzyć powierzchnię pokoju, ogrodu, a nawet kartki papieru? W klasie 5 zaczynamy przygodę z figurami geometrycznymi i ich polami. To może wydawać się trudne, ale obiecuję – z odpowiednim podejściem i kilkoma prostymi wzorami, stanie się to bułka z masłem!

Wiem, że nauka nowych wzorów bywa frustrująca, szczególnie kiedy wydają się abstrakcyjne. Ale pomyśl o tym jak o mapie skarbów. Każdy wzór to klucz, który otwiera drzwi do rozwiązania konkretnego problemu. Bez obaw, przeprowadzę Cię przez to krok po kroku.

Podstawowe figury i ich pola

Kwadrat

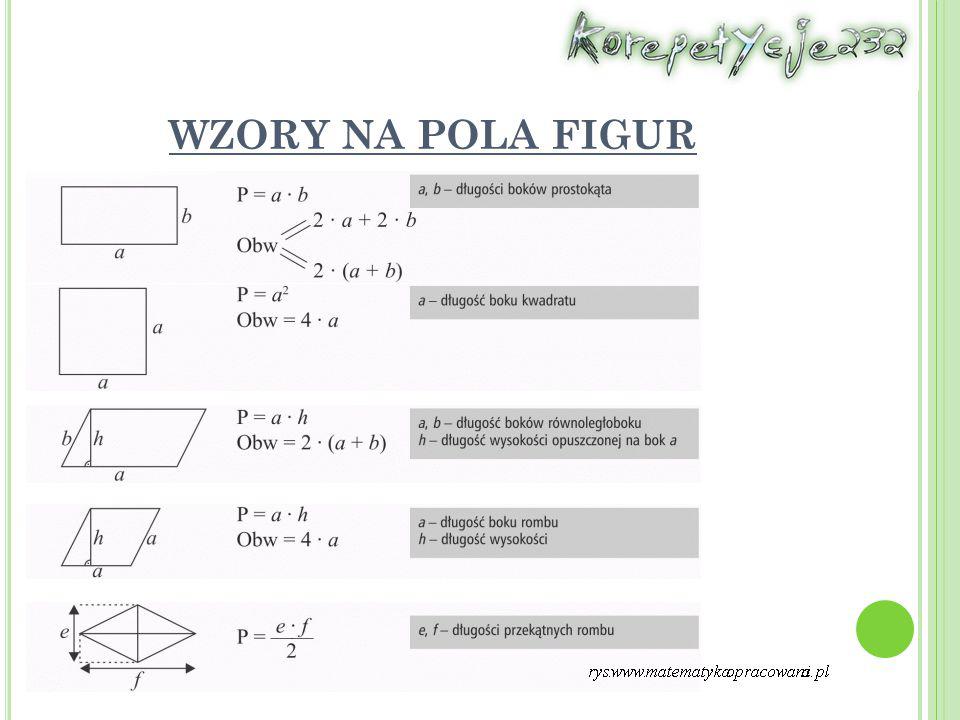
Kwadrat to figura, którą wszyscy dobrze znamy. Ma cztery równe boki i cztery kąty proste. Jak obliczyć jego pole?

Wzór jest bardzo prosty:

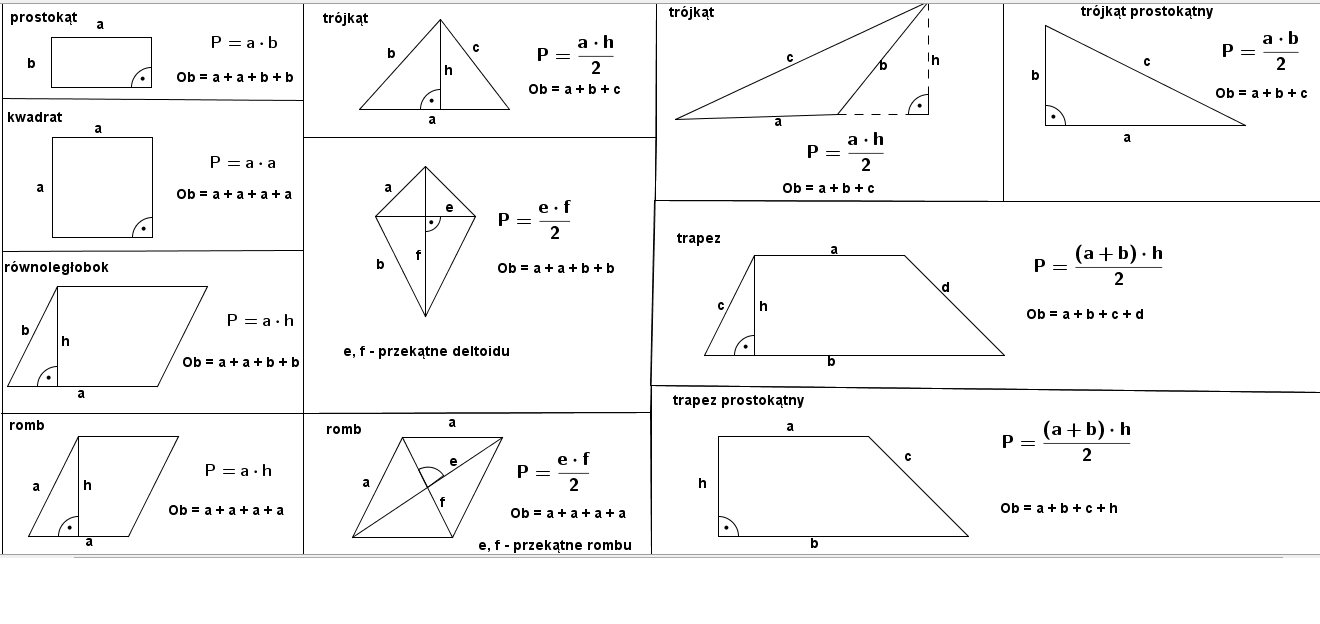
Pole kwadratu = bok * bok, czyli P = a * a, gdzie "a" to długość boku.

Przykład: Jeżeli bok kwadratu ma 5 cm, to jego pole wynosi 5 cm * 5 cm = 25 cm². Pamiętaj, że jednostką pola jest jednostka długości do kwadratu (np. cm², m², km²).

Prostokąt

Prostokąt, podobnie jak kwadrat, ma cztery kąty proste, ale jego boki nie muszą być równe. Ma dwie pary boków o jednakowej długości. Jak obliczyć jego pole?

Wzór jest równie prosty:

Pole prostokąta = długość * szerokość, czyli P = a * b, gdzie "a" to długość, a "b" to szerokość.

Przykład: Jeżeli długość prostokąta wynosi 8 cm, a szerokość 3 cm, to jego pole wynosi 8 cm * 3 cm = 24 cm².

Równoległobok

Równoległobok przypomina trochę prostokąt, ale jego kąty nie muszą być proste. Ma dwie pary boków równoległych. Do obliczenia pola potrzebujemy długości podstawy i wysokości.

Ważne! Wysokość to odcinek prostopadły do podstawy, łączący podstawę z przeciwległym bokiem.

Wzór na pole równoległoboku:

Pole równoległoboku = podstawa * wysokość, czyli P = a * h, gdzie "a" to długość podstawy, a "h" to wysokość opuszczona na tę podstawę.

Przykład: Jeżeli podstawa równoległoboku ma 10 cm, a wysokość opuszczona na tę podstawę ma 4 cm, to jego pole wynosi 10 cm * 4 cm = 40 cm².

Trójkąt

Trójkąt to figura o trzech bokach i trzech kątach. Obliczanie jego pola wymaga odrobinę więcej uwagi.

Podobnie jak w równoległoboku, potrzebujemy długości podstawy i wysokości. Wysokość to odcinek prostopadły do podstawy, łączący podstawę z wierzchołkiem leżącym naprzeciwko.

Wzór na pole trójkąta:

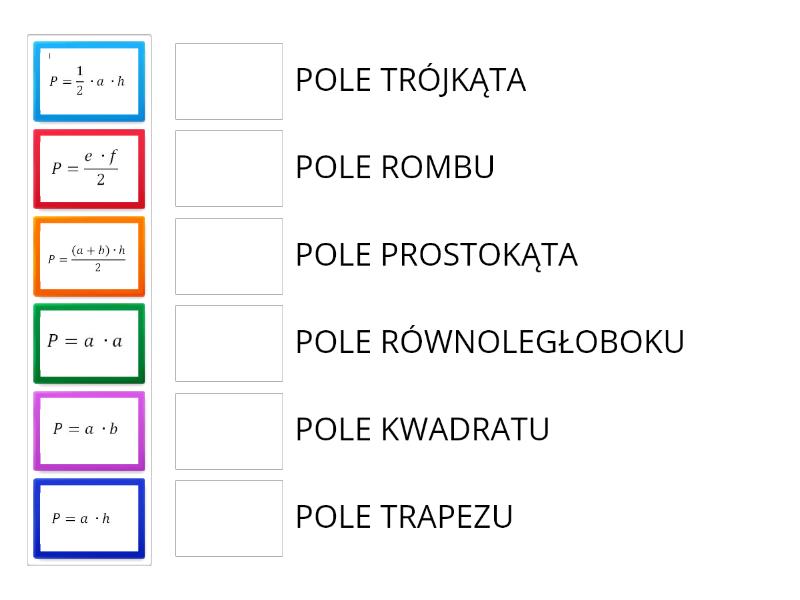
Pole trójkąta = (podstawa * wysokość) / 2, czyli P = (a * h) / 2, gdzie "a" to długość podstawy, a "h" to wysokość opuszczona na tę podstawę.

Dlaczego dzielimy przez 2? Wyobraź sobie, że rysujesz drugi identyczny trójkąt i doklejasz go do pierwszego tak, aby powstał równoległobok. Pole tego równoległoboku to a * h, a pole jednego trójkąta to połowa tego pola. To ważna wizualizacja!

Przykład: Jeżeli podstawa trójkąta ma 6 cm, a wysokość opuszczona na tę podstawę ma 7 cm, to jego pole wynosi (6 cm * 7 cm) / 2 = 42 cm² / 2 = 21 cm².

Trapez

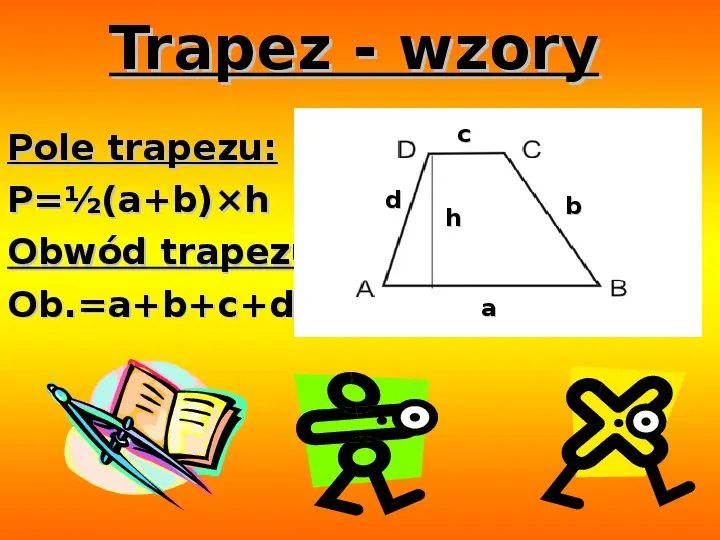
Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Te równoległe boki nazywamy podstawami, a pozostałe dwa boki to ramiona.

Do obliczenia pola trapezu potrzebujemy długości obu podstaw i wysokości. Wysokość to odcinek prostopadły do obu podstaw, łączący je.

Wzór na pole trapezu:

Pole trapezu = ((podstawa a + podstawa b) * wysokość) / 2, czyli P = ((a + b) * h) / 2, gdzie "a" i "b" to długości podstaw, a "h" to wysokość.

Przykład: Jeżeli jedna podstawa trapezu ma 4 cm, druga podstawa ma 8 cm, a wysokość wynosi 5 cm, to jego pole wynosi ((4 cm + 8 cm) * 5 cm) / 2 = (12 cm * 5 cm) / 2 = 60 cm² / 2 = 30 cm².

Praktyczne wskazówki i triki

• Zawsze zapisuj wzór przed podstawieniem wartości. To pomoże Ci uniknąć pomyłek.
• Sprawdzaj jednostki. Upewnij się, że wszystkie długości są podane w tej samej jednostce (np. cm, m). Jeśli nie, zamień je!
• Rysuj diagramy. Wizualizacja figury geometrycznej i zaznaczenie na niej danych (długości boków, wysokość) ułatwi Ci rozwiązanie zadania.
• Ćwicz, ćwicz i jeszcze raz ćwicz. Im więcej zadań rozwiążesz, tym lepiej zapamiętasz wzory i zrozumiesz, jak je stosować.
• Nie bój się pytać! Jeżeli masz wątpliwości, poproś nauczyciela, rodzica lub kolegę o pomoc.

Pamiętaj, że matematyka to nie tylko wzory, ale przede wszystkim logiczne myślenie. Zrozumienie, dlaczego dany wzór działa, jest ważniejsze niż samo zapamiętanie go na pamięć. Spróbuj zrozumieć, skąd się biorą te wzory!

Na przykład, wracając do trójkąta, pomyśl o tym, że możesz przekształcić go w prostokąt o połowie wysokości. Wtedy pole takiego prostokąta byłoby równe a * (h/2), co jest równoważne (a * h) / 2. To wizualizacja!

Gdzie to wykorzystasz w życiu?

Obliczanie pól figur przydaje się w wielu sytuacjach. Na przykład:

• Planowanie remontu: Obliczenie, ile farby potrzebujesz do pomalowania ściany (prostokąt), albo ile płytek podłogowych potrzeba do wyłożenia podłogi (kwadrat, prostokąt).
• Projektowanie ogrodu: Obliczenie powierzchni trawnika (dowolna figura) potrzebnej do wysiania trawy.
• Krawiectwo: Obliczenie ilości materiału potrzebnego do uszycia ubrania (często używa się wzorów na pola różnych figur).
• Gotowanie: Określenie, ile ciasta potrzebujesz, aby wypełnić blachę o konkretnym kształcie (np. prostokątną lub okrągłą – okrąg poznamy później!).

Jak widzisz, znajomość wzorów na pola figur to praktyczna umiejętność, która przyda Ci się przez całe życie!

Podsumowanie

Nauka wzorów na pola figur w klasie 5 to ważny krok w Twojej edukacji matematycznej. Pamiętaj o podstawowych figurach: kwadracie, prostokącie, równoległoboku, trójkącie i trapezie. Naucz się wzorów, ćwicz regularnie i nie bój się zadawać pytań. Z czasem zobaczysz, że to naprawdę proste!

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak obliczać pola figur. Powodzenia w nauce i nie zapominaj, że matematyka może być fascynująca!