Wzory Na Obliczanie Pola Figur

Zastanawiałeś się kiedyś, jak obliczyć powierzchnię Twojego pokoju, żeby kupić odpowiednią ilość farby? A może potrzebujesz wiedzieć, ile materiału potrzeba na uszycie obrusu w kształcie koła? Obliczanie pola figur geometrycznych jest przydatne w wielu aspektach życia, od remontów po szycie ubrań i planowanie ogrodu. Ten artykuł jest skierowany do uczniów, studentów, majsterkowiczów i każdego, kto chce odświeżyć lub poszerzyć swoją wiedzę z zakresu geometrii. Przyjrzymy się najważniejszym wzorom i pokażemy, jak je stosować w praktyce. Zatem, zaczynajmy!

Podstawowe Figury i Ich Pola

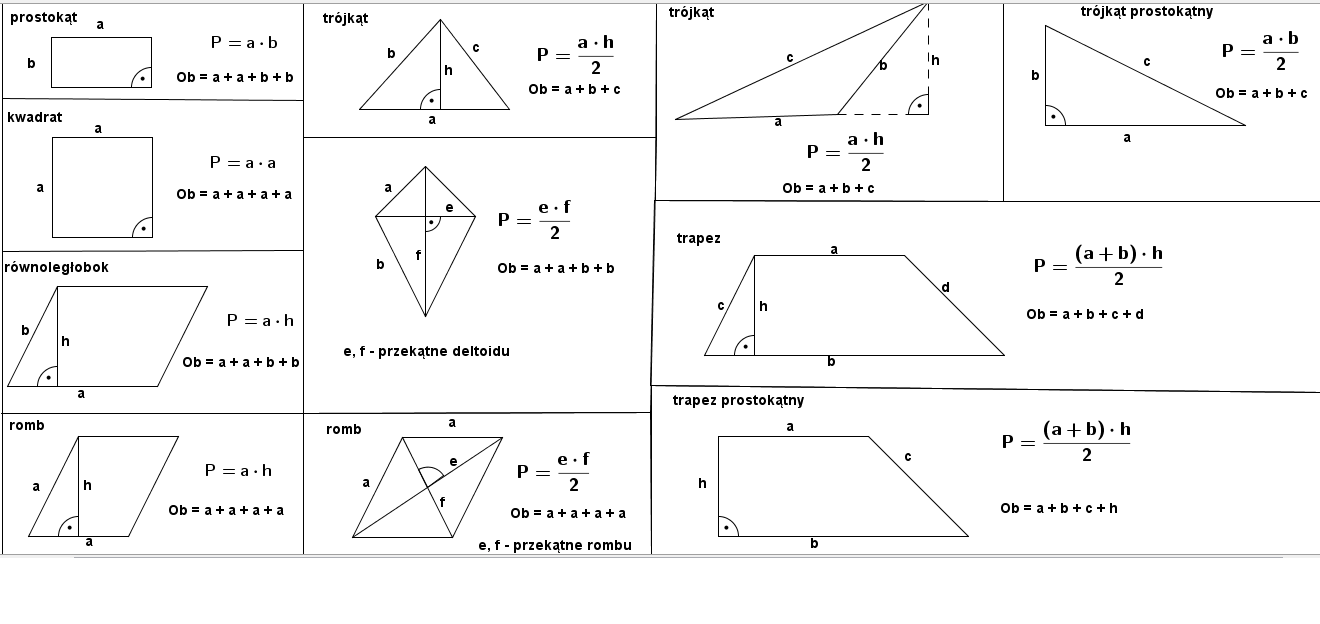
Zanim przejdziemy do bardziej skomplikowanych kształtów, warto przypomnieć sobie podstawy. Znajomość wzorów na pole kwadratu, prostokąta i trójkąta jest kluczowa do zrozumienia bardziej złożonych zagadnień. Poniżej znajdziesz omówienie najważniejszych figur:

Kwadrat

Kwadrat to czworokąt, który ma wszystkie boki równe i wszystkie kąty proste. Obliczenie jego pola jest bardzo proste:

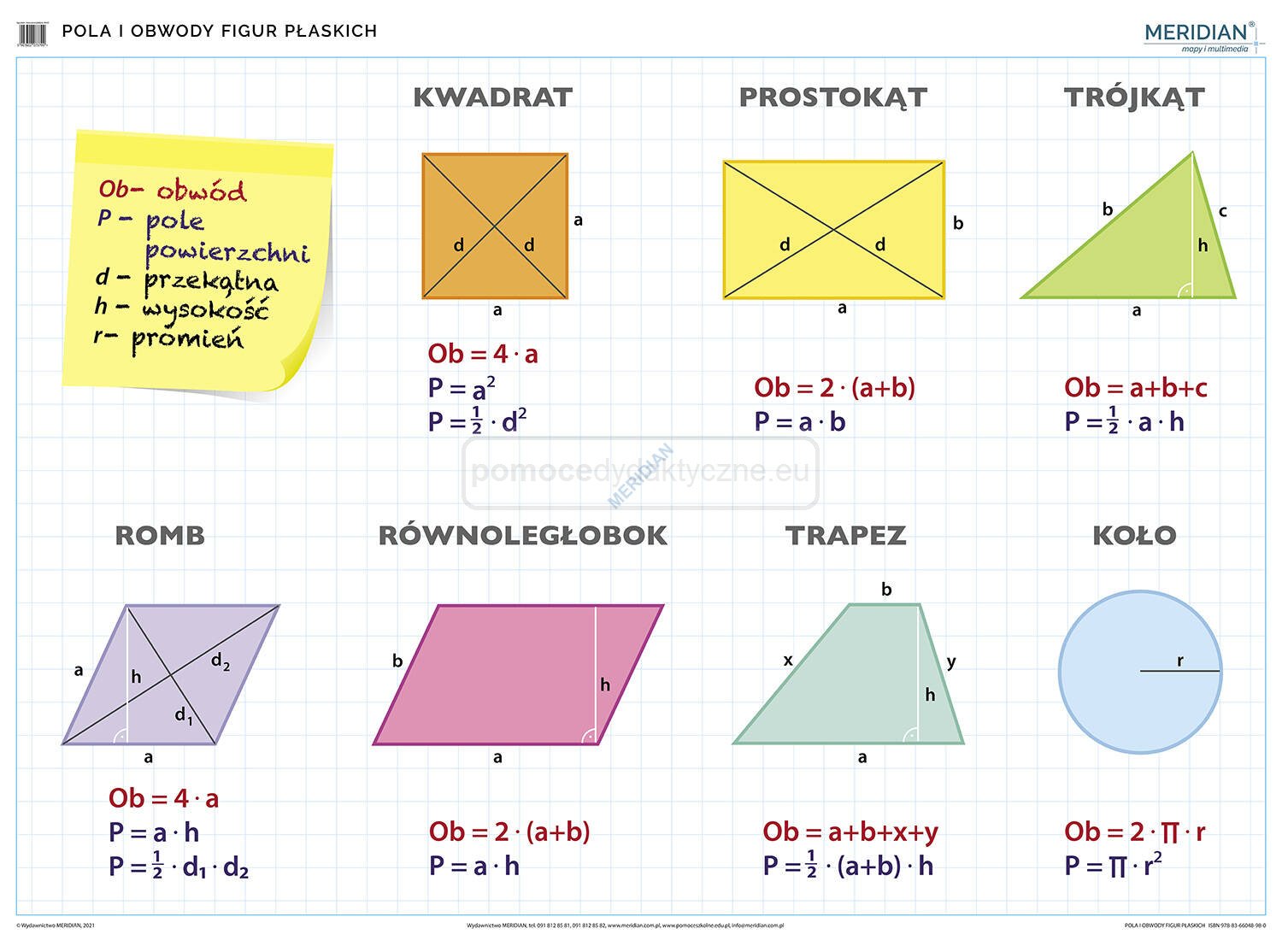
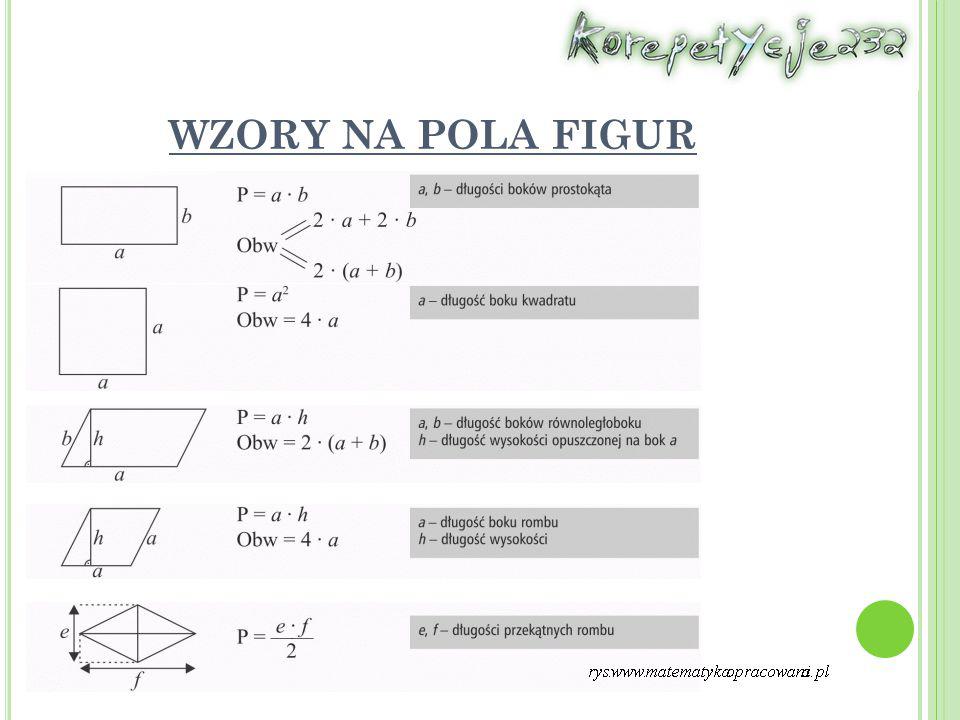
Wzór: P = a², gdzie 'a' to długość boku kwadratu.
Przykład: Jeśli bok kwadratu ma długość 5 cm, to jego pole wynosi P = 5² = 25 cm².

Prostokąt

Prostokąt to czworokąt, który ma wszystkie kąty proste. Jego pole obliczamy mnożąc długość jednego boku przez długość drugiego, sąsiedniego boku.

Wzór: P = a * b, gdzie 'a' i 'b' to długości boków prostokąta.
Przykład: Prostokąt ma boki o długościach 8 cm i 3 cm. Jego pole wynosi P = 8 * 3 = 24 cm².

Trójkąt

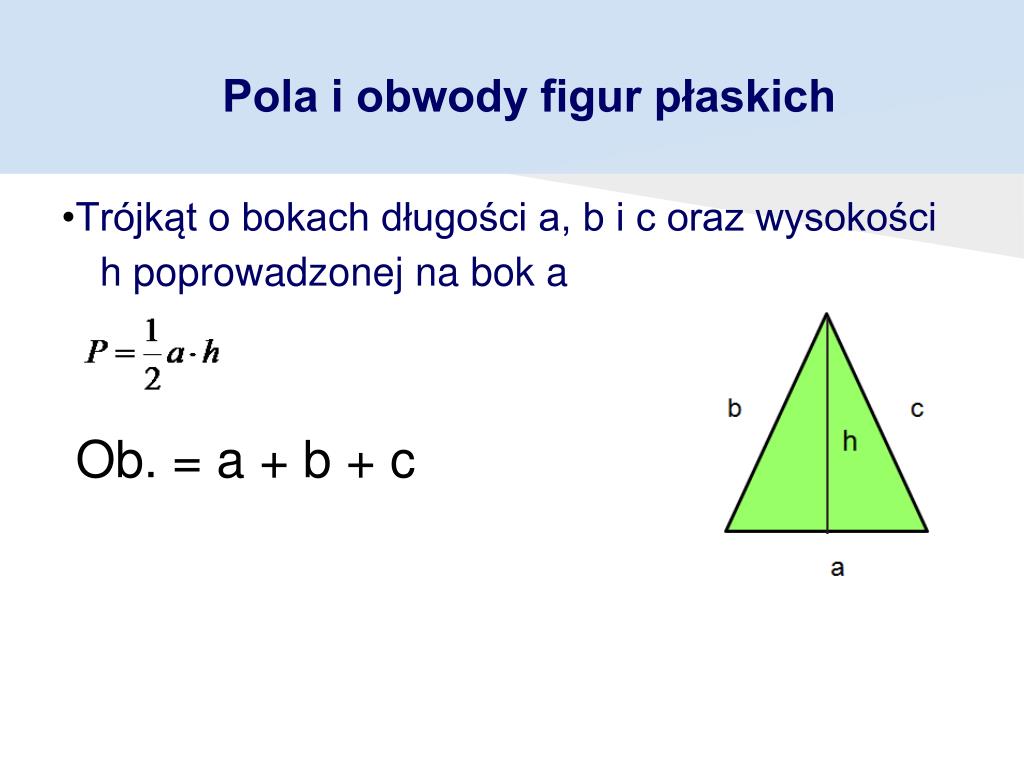
Obliczanie pola trójkąta wymaga znajomości długości podstawy i wysokości opuszczonej na tę podstawę. Wysokość jest odcinkiem prostopadłym do podstawy, łączącym ją z wierzchołkiem przeciwnym.

Wzór: P = (1/2) * a * h, gdzie 'a' to długość podstawy trójkąta, a 'h' to wysokość opuszczona na tę podstawę.
Przykład: Trójkąt ma podstawę o długości 6 cm i wysokość o długości 4 cm. Jego pole wynosi P = (1/2) * 6 * 4 = 12 cm².

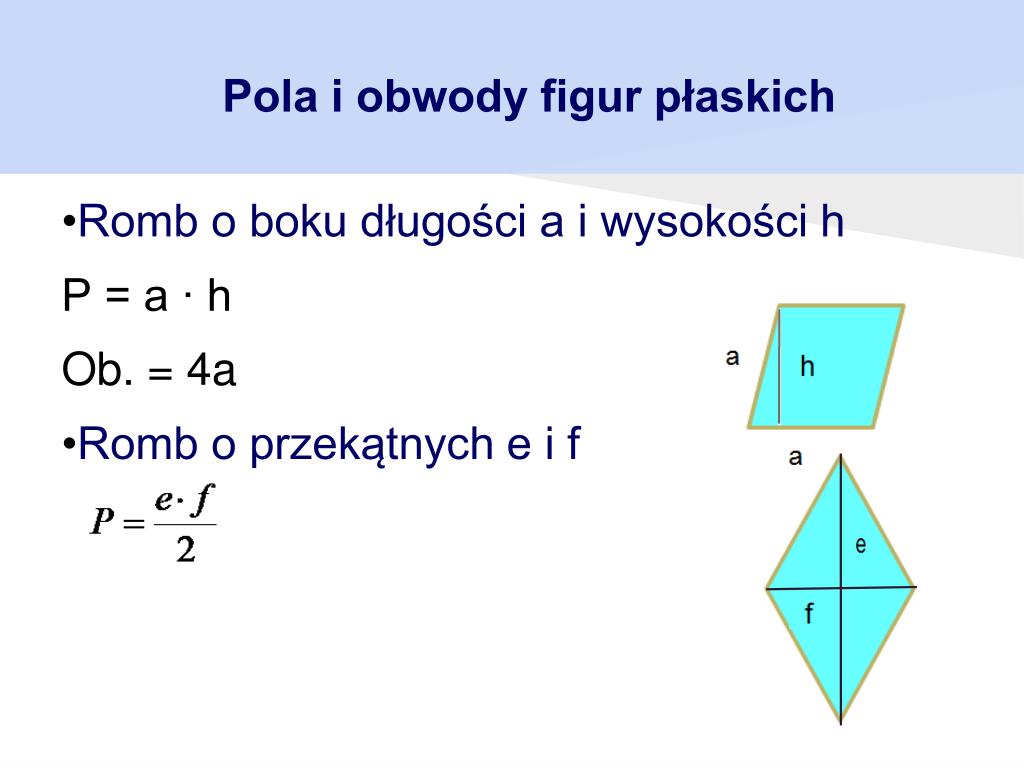
Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Jego pole obliczamy podobnie jak pole prostokąta, mnożąc długość boku przez wysokość opuszczoną na ten bok.

Wzór: P = a * h, gdzie 'a' to długość boku równoległoboku, a 'h' to wysokość opuszczona na ten bok.
Przykład: Równoległobok ma bok o długości 7 cm i wysokość opuszczoną na ten bok o długości 5 cm. Jego pole wynosi P = 7 * 5 = 35 cm².

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych (zwanych podstawami). Jego pole obliczamy korzystając ze średniej długości podstaw i wysokości.

Wzór: P = (1/2) * (a + b) * h, gdzie 'a' i 'b' to długości podstaw trapezu, a 'h' to wysokość trapezu.
Przykład: Trapez ma podstawy o długościach 9 cm i 5 cm oraz wysokość o długości 3 cm. Jego pole wynosi P = (1/2) * (9 + 5) * 3 = 21 cm².

Koło

Koło to zbiór punktów na płaszczyźnie, których odległość od ustalonego punktu (środka koła) jest nie większa niż dana odległość (promień koła).

Wzór: P = π * r², gdzie 'π' (pi) to stała matematyczna w przybliżeniu równa 3.14159, a 'r' to długość promienia koła.
Przykład: Koło ma promień o długości 4 cm. Jego pole wynosi P = π * 4² ≈ 3.14159 * 16 ≈ 50.27 cm².

Bardziej Złożone Figury

Często spotykamy się z figurami, które nie są prostymi kwadratami, prostokątami czy kołami. W takich przypadkach musimy zastosować sprytne metody, aby obliczyć ich pole. Dwa popularne podejścia to:

Rozkład na prostsze figury: Podziel złożoną figurę na mniejsze, prostsze figury, których pole potrafisz obliczyć (np. prostokąty, trójkąty). Następnie zsumuj pola tych mniejszych figur, aby otrzymać pole całej figury.
Uzupełnianie do prostszych figur: Dodaj do figury brakujące elementy, aby utworzyć prostszą figurę (np. prostokąt). Oblicz pole tej większej figury, a następnie odejmij pole dodanych elementów.

Przykład: Figura w Kształcie Litery L

Wyobraź sobie figurę w kształcie litery L. Możemy ją podzielić na dwa prostokąty. Oblicz pole każdego prostokąta osobno, a następnie zsumuj wyniki. Na przykład, jeśli jeden prostokąt ma wymiary 2 cm x 5 cm, a drugi 3 cm x 4 cm, to pola wynoszą odpowiednio 10 cm² i 12 cm². Pole całej figury L wynosi zatem 10 + 12 = 22 cm².

Wzór Herona na Pole Trójkąta

Jeśli znasz długości wszystkich boków trójkąta, ale nie znasz jego wysokości, możesz skorzystać z wzoru Herona. Wzór ten pozwala obliczyć pole trójkąta na podstawie samych długości boków.

Krok 1: Oblicz połowę obwodu trójkąta, zwaną również semiperymetrem (s): s = (a + b + c) / 2, gdzie 'a', 'b' i 'c' to długości boków trójkąta.
Krok 2: Zastosuj wzór Herona: P = √[s * (s - a) * (s - b) * (s - c)]

Przykład

Trójkąt ma boki o długościach 5 cm, 6 cm i 7 cm. Obliczamy semiperymetr: s = (5 + 6 + 7) / 2 = 9 cm. Następnie, stosujemy wzór Herona: P = √[9 * (9 - 5) * (9 - 6) * (9 - 7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm².

Praktyczne Zastosowania

Jak już wspomnieliśmy na początku, znajomość wzorów na obliczanie pola figur ma wiele praktycznych zastosowań:

Remonty: Obliczanie powierzchni ścian do malowania, podłóg do wyłożenia panelami, czy płytek do położenia w łazience.
Ogród: Planowanie rabat kwiatowych, trawników, czy powierzchni ścieżek.
Krawiectwo: Obliczanie ilości materiału potrzebnego do uszycia ubrania, obrusu, czy zasłon.
Budownictwo: Obliczanie powierzchni dachu, ścian budynku, czy fundamentów.
Inżynieria: Obliczanie powierzchni przekrojów elementów konstrukcyjnych, powierzchni skrzydeł samolotu, czy powierzchni turbin wiatrowych.

Pomyśl o sytuacji, w której chcesz kupić dywan do salonu. Mierząc długość i szerokość salonu, możesz obliczyć jego powierzchnię (pole prostokąta). Dzięki temu będziesz wiedział, jak duży dywan potrzebujesz, aby odpowiednio wypełnił przestrzeń.

Pamiętaj! Jednostki Miar

Bardzo ważne jest, aby pamiętać o jednostkach miar. Jeśli mierzysz długości w centymetrach (cm), to pole będzie wyrażone w centymetrach kwadratowych (cm²). Podobnie, jeśli mierzysz w metrach (m), to pole będzie wyrażone w metrach kwadratowych (m²). Upewnij się, że wszystkie wymiary są wyrażone w tej samej jednostce, zanim zaczniesz obliczenia. Jeśli masz wymiary w różnych jednostkach, zamień je na jedną wspólną jednostkę (np. zamień centymetry na metry) przed obliczeniem pola.

Wskazówki i Triki

Zawsze rysuj schemat: Narysowanie figury, której pole chcesz obliczyć, pomoże Ci lepiej zrozumieć problem i zidentyfikować potrzebne wymiary.
Sprawdzaj jednostki: Upewnij się, że wszystkie wymiary są wyrażone w tej samej jednostce miary.
Wykorzystaj wzory online: Istnieje wiele kalkulatorów online, które mogą pomóc Ci obliczyć pole różnych figur. Możesz je wykorzystać do sprawdzenia swoich obliczeń.
Ćwicz! Im więcej będziesz ćwiczył, tym lepiej opanujesz wzory na obliczanie pola figur.

Podsumowanie

Obliczanie pola figur geometrycznych jest umiejętnością niezwykle przydatną w życiu codziennym. Znajomość podstawowych wzorów na pole kwadratu, prostokąta, trójkąta, równoległoboku, trapezu i koła, a także umiejętność rozkładania bardziej złożonych figur na prostsze, pozwoli Ci rozwiązywać wiele praktycznych problemów. Pamiętaj o jednostkach miar i zawsze sprawdzaj swoje obliczenia! Mam nadzieję, że ten artykuł pomógł Ci odświeżyć lub poszerzyć Twoją wiedzę z zakresu geometrii i zachęcił do dalszego zgłębiania tego fascynującego tematu. Teraz śmiało, idź i zmierz świat!