Wzory Na Obliczanie Pól Figur

Czy kiedykolwiek zastanawiałeś się, jak obliczyć ilość farby potrzebnej do pomalowania ściany, albo ile materiału potrzeba do uszycia obrusu na stół? A może musisz policzyć, ile trawy kupić, żeby obsiać ogródek? W każdym z tych przypadków niezbędna jest znajomość wzorów na obliczanie pól figur. To nie tylko sucha teoria z podręcznika matematyki – to praktyczna umiejętność, która przydaje się w wielu aspektach codziennego życia.

Dlaczego Znajomość Wzorów na Pola Figur Jest Ważna?

Wiele osób może myśleć, że obliczanie pól figur to coś, co potrzebne jest tylko uczniom i studentom, albo inżynierom i architektom. To prawda, że te grupy zawodowe intensywnie korzystają z tej wiedzy, ale korzyści są o wiele szersze:

Planowanie remontów i dekoracji: Obliczenie powierzchni ścian, podłóg, sufitów, aby oszacować koszty materiałów (farby, tapety, płytki, panele).
Prace ogrodnicze: Obliczenie powierzchni trawnika, rabatek, klombów, aby dobrać odpowiednią ilość nasion, nawozów, ziemi.
Projektowanie i szycie: Obliczenie powierzchni materiału potrzebnego do uszycia ubrań, obrusów, zasłon.
Budownictwo: Obliczenie powierzchni dachu, ścian, fundamentów, aby oszacować koszty budowy i dobrać odpowiednie materiały.
Sztuka i rzemiosło: Obliczenie powierzchni płótna, papieru, drewna potrzebnego do stworzenia dzieła sztuki lub rękodzieła.

Bez znajomości tych wzorów, ryzykujesz przepłacenie za materiały, marnowanie zasobów i frustrację wynikającą z niedoszacowania lub przeszacowania potrzeb. Wiedza ta daje Ci kontrolę nad swoimi projektami i pozwala podejmować bardziej świadome decyzje.

Podstawowe Wzory na Pola Figur

Przyjrzyjmy się teraz najważniejszym wzorom, które warto znać na pamięć:

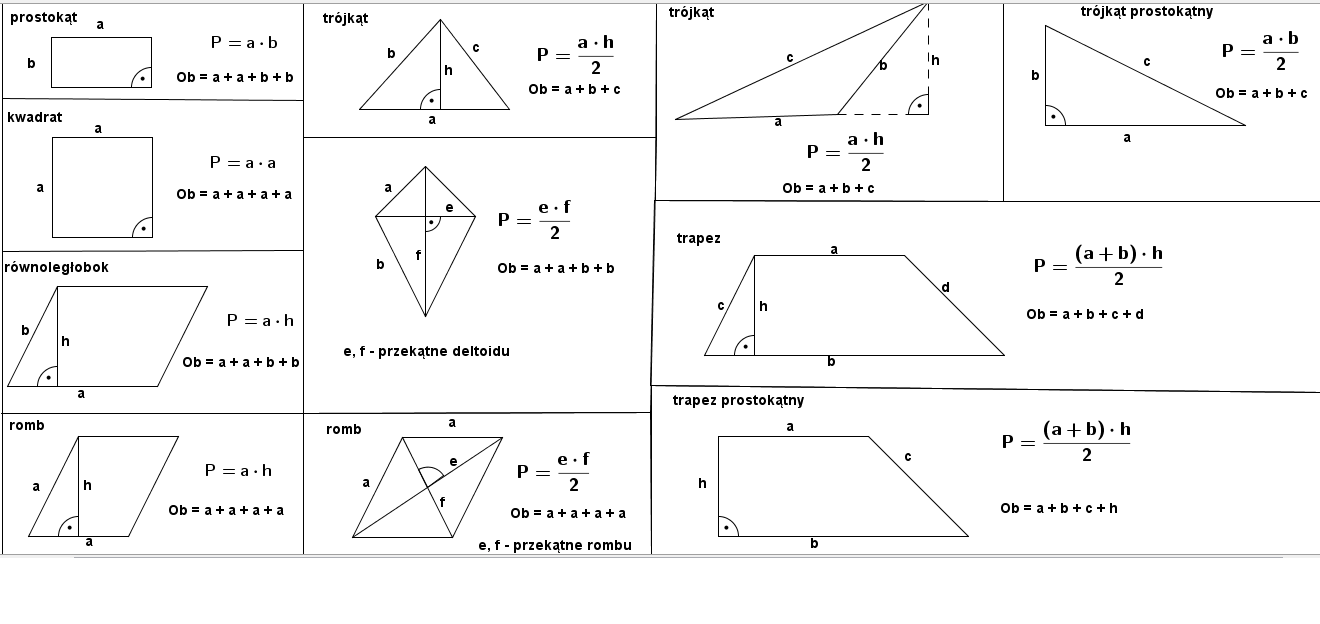
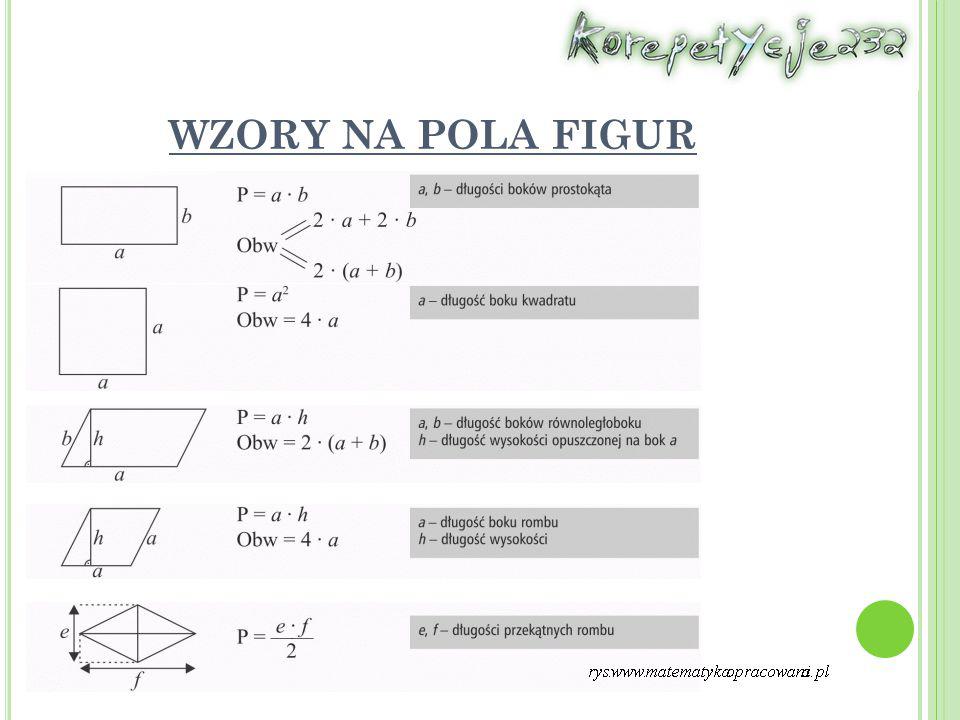
Kwadrat

Najprostsza figura. Wszystkie boki są równe. Pole kwadratu obliczamy, podnosząc długość boku do kwadratu:

P = a², gdzie 'a' to długość boku.

Przykład: Kwadrat o boku 5 cm ma pole 25 cm².

Prostokąt

Ma dwa boki o tej samej długości. Pole prostokąta obliczamy, mnożąc długość przez szerokość:

P = a * b, gdzie 'a' to długość, a 'b' to szerokość.

Przykład: Prostokąt o długości 8 cm i szerokości 3 cm ma pole 24 cm².

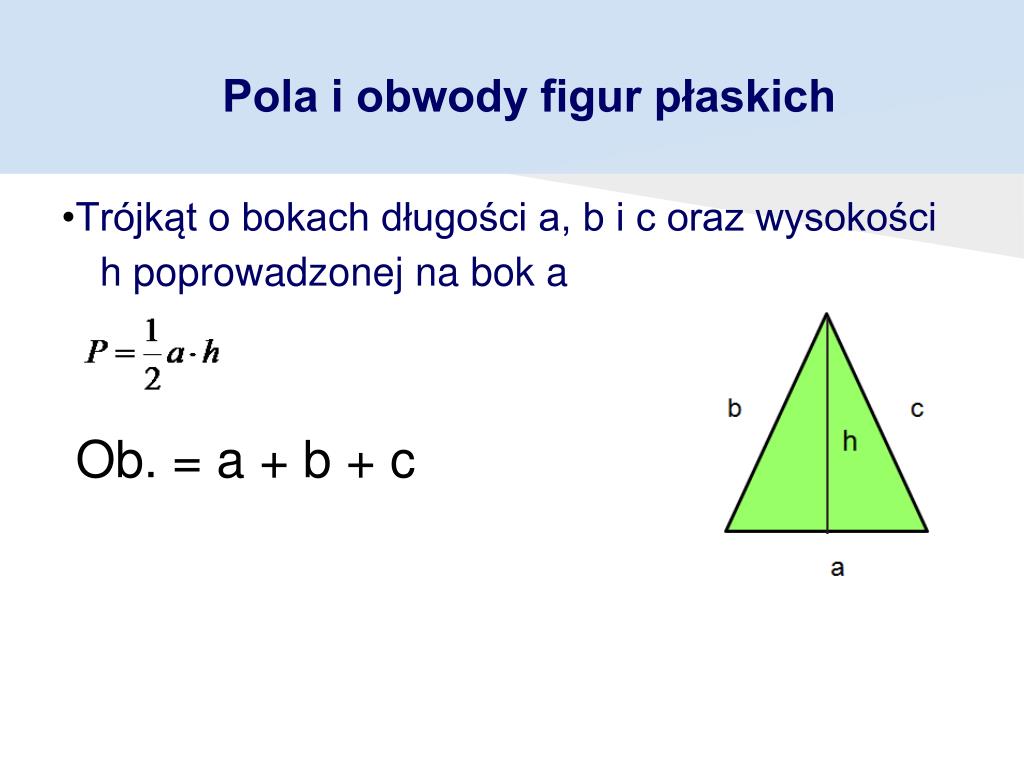
Trójkąt

Wzór podstawowy: P = (a * h) / 2, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.

Istnieją różne rodzaje trójkątów, ale ten wzór jest uniwersalny. Ważne jest, aby wysokość była prostopadła do podstawy.

Dla trójkąta równobocznego o boku 'a': P = (a² * √3) / 4.

Dla trójkąta prostokątnego o przyprostokątnych 'a' i 'b': P = (a * b) / 2.

Równoległobok

Pole równoległoboku obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę:

P = a * h, gdzie 'a' to długość podstawy, a 'h' to wysokość.

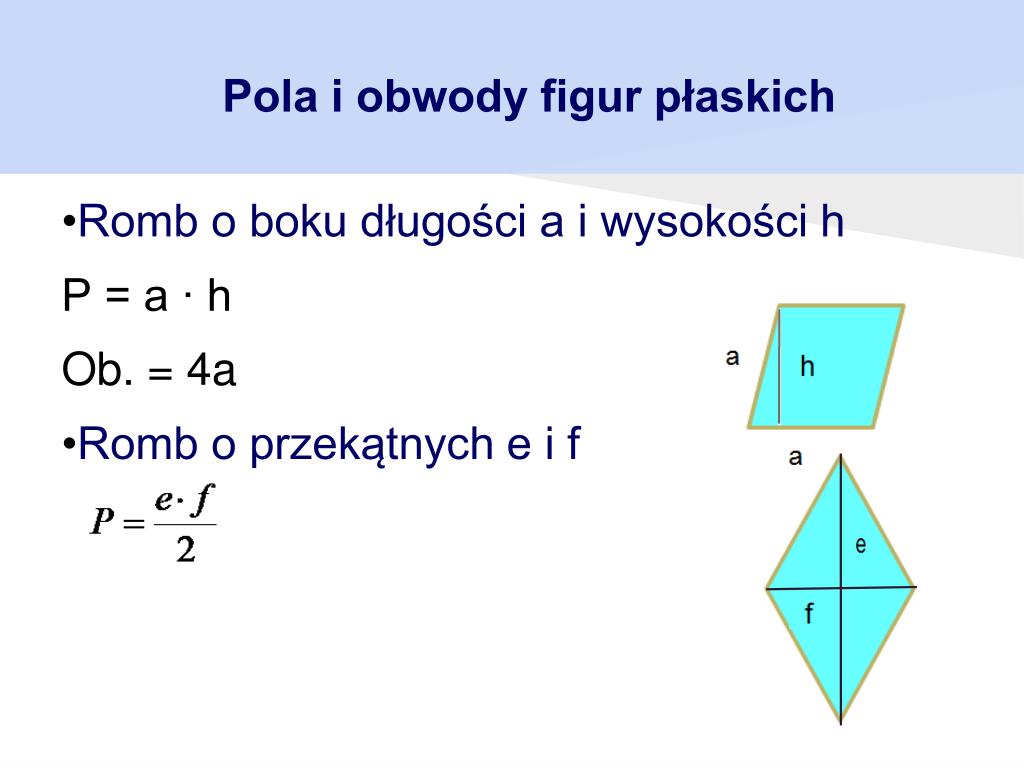
Romb

Romb to równoległobok o wszystkich bokach równych. Można go obliczyć na dwa sposoby:

Tak jak równoległobok: P = a * h
Znając długości przekątnych: P = (d₁ * d₂) / 2, gdzie d₁ i d₂ to długości przekątnych.

Trapez

Trapez ma dwie podstawy (a i b) i wysokość (h). Pole obliczamy ze wzoru:

P = ((a + b) * h) / 2

Koło

Pole koła obliczamy za pomocą promienia (r) i liczby pi (π ≈ 3.14159):

P = π * r²

Przeciwwskazania i Wyjątki

Oczywiście, nie zawsze wszystko jest tak proste, jak w podręczniku. Istnieją sytuacje, w których te wzory mogą nie wystarczyć:

Nieregularne kształty: Jeśli masz do czynienia z figurą o nieregularnym kształcie, często trzeba ją podzielić na mniejsze, bardziej regularne figury, obliczyć pole każdej z nich osobno, a następnie zsumować wyniki. Można również zastosować metody przybliżone, np. metodę kratek.
Figury trójwymiarowe: Te wzory dotyczą figur płaskich. Do obliczania powierzchni brył trójwymiarowych (np. sześcianu, walca, kuli) potrzebne są inne wzory.
Błędy pomiarowe: Nawet najdokładniejsze pomiary obarczone są pewnym błędem. Trzeba o tym pamiętać, interpretując wyniki obliczeń.

Niektórzy twierdzą, że w dobie komputerów i specjalistycznego oprogramowania znajomość tych wzorów jest zbędna. Można po prostu wpisać dane do programu, a on wszystko policzy. To prawda, że programy ułatwiają pracę, ale zrozumienie zasad, na których opierają się obliczenia, jest niezwykle ważne. Pozwala to na weryfikację wyników, wykrywanie błędów i podejmowanie bardziej świadomych decyzji.

Jak Ułatwić Sobie Zapamiętywanie Wzorów?

Zapamiętanie wszystkich wzorów na pamięć może wydawać się trudne. Oto kilka sposobów, które mogą Ci pomóc:

Powtarzanie: Regularne powtarzanie wzorów utrwala je w pamięci.
Praktyczne zastosowanie: Najlepiej zapamiętuje się to, co się wykorzystuje w praktyce. Staraj się stosować wzory w realnych sytuacjach, np. podczas planowania remontu lub ogrodu.
Tworzenie skojarzeń: Skojarz wzór z jakąś łatwą do zapamiętania historią, obrazem lub piosenką.
Rysunki i diagramy: Narysuj figurę i zaznacz na niej odpowiednie wymiary. To ułatwi Ci zrozumienie, skąd bierze się wzór.
Aplikacje i strony internetowe: Korzystaj z aplikacji i stron internetowych, które oferują interaktywne ćwiczenia i testy z zakresu obliczania pól figur.

Podsumowanie i Co Dalej?

Znajomość wzorów na obliczanie pól figur to nieoceniona umiejętność, która przydaje się w wielu dziedzinach życia. Od planowania remontu, przez prace ogrodnicze, po projektowanie ubrań – ta wiedza pozwala Ci oszczędzać pieniądze, czas i nerwy. Nie zrażaj się, jeśli na początku wydaje Ci się to trudne. Ćwicz, eksperymentuj i staraj się stosować te wzory w praktyce, a z czasem staną się one dla Ciebie naturalne jak tabliczka mnożenia.

Czy masz już pomysł, jak wykorzystasz swoją nową wiedzę o obliczaniu pól figur w najbliższym czasie? Może zaplanujesz nową aranżację ogrodu, a może obliczysz, ile materiału potrzebujesz na nową zasłonę do okna? Niech to będzie Twój pierwszy krok w kierunku praktycznego wykorzystania matematyki!