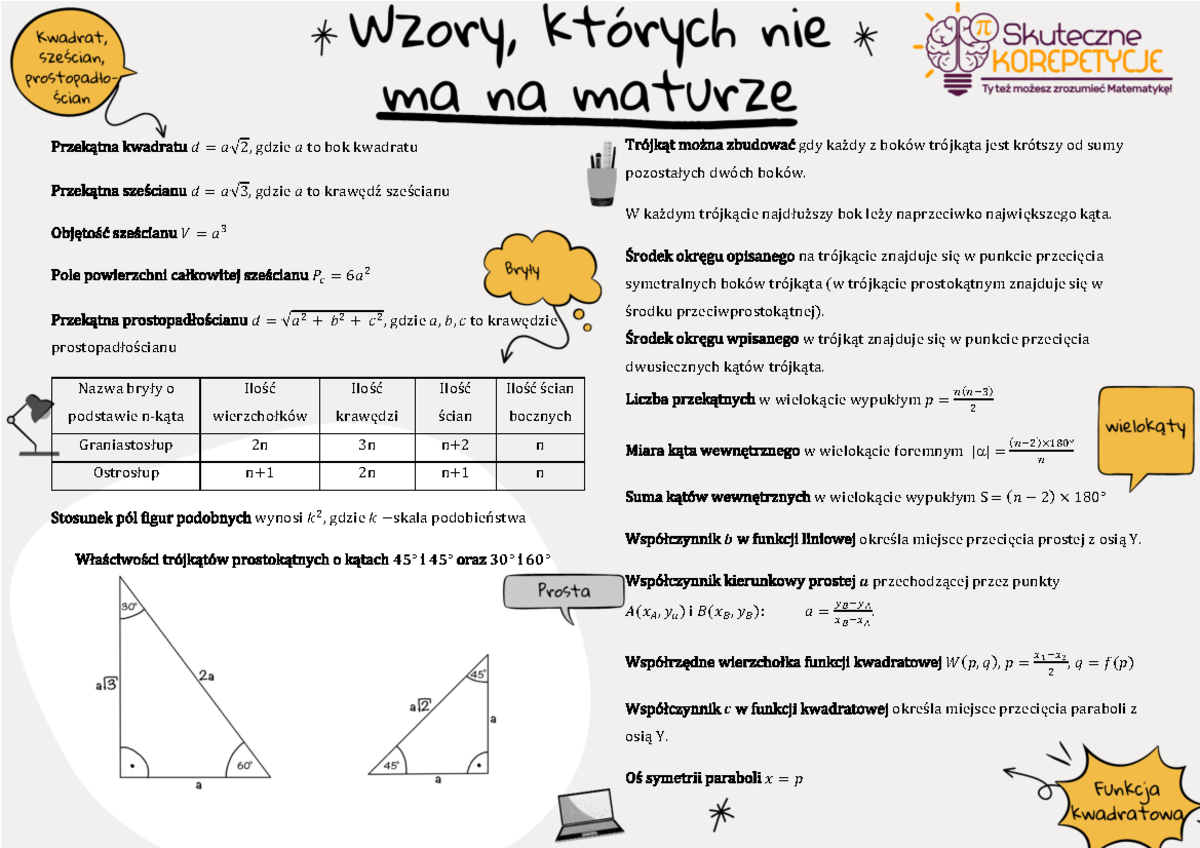
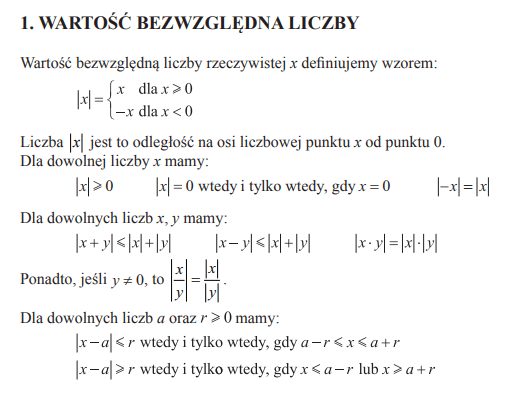Wzory Na Egzamin ósmoklasisty 2022

Zdaję sobie sprawę, jak stresujący może być egzamin ósmoklasisty. Mnóstwo materiału, nerwy, presja… Najważniejsze to zachować spokój i dobrze się przygotować. Jednym z kluczowych elementów tej przygotowywania jest znajomość wzorów matematycznych. W tym artykule postaram się usystematyzować wszystkie wzory, które musisz znać na egzamin ósmoklasisty z matematyki w 2022 roku. Pamiętaj, że znajomość wzorów to dopiero połowa sukcesu – trzeba jeszcze umieć je prawidłowo zastosować w zadaniach. No to zaczynamy!

Liczby i działania

Choć wydaje się to oczywiste, upewnij się, że masz opanowane podstawowe działania: dodawanie, odejmowanie, mnożenie i dzielenie. Pamiętaj o kolejności wykonywania działań – nawiasy, potęgowanie/pierwiastkowanie, mnożenie/dzielenie, dodawanie/odejmowanie.

Działania na ułamkach

Ułamki zwykłe:

Dodawanie/odejmowanie: a/b + c/b = (a+c)/b (musisz mieć wspólny mianownik!)
Mnożenie: a/b * c/d = (a*c)/(b*d)
Dzielenie: a/b : c/d = a/b * d/c = (a*d)/(b*c) (dzielenie to mnożenie przez odwrotność!)

Ułamki dziesiętne: Tutaj przydaje się umiejętność zamiany ułamków zwykłych na dziesiętne i odwrotnie. Mnożenie i dzielenie przez 10, 100, 1000, etc. to po prostu przesuwanie przecinka.

Potęgi i pierwiastki

Potęgi:

aⁿ * a^m = a^n+m (mnożenie potęg o tej samej podstawie)
aⁿ / a^m = a^n-m (dzielenie potęg o tej samej podstawie)
(aⁿ)^m = a^n*m (potęgowanie potęgi)
(a * b)ⁿ = aⁿ * bⁿ (potęgowanie iloczynu)
(a / b)ⁿ = aⁿ / bⁿ (potęgowanie ilorazu)
a⁰ = 1 (każda liczba podniesiona do potęgi zerowej daje 1)
a^-n = 1 / aⁿ (potęga ujemna)

Pierwiastki:

√a * √b = √(a * b)
√a / √b = √(a / b)

Pamiętaj, że nie można dodawać ani odejmować pierwiastków, chyba że pod pierwiastkiem jest taka sama liczba!

Procenty

Procent to inaczej setna część całości. Kluczowe jest zrozumienie, jak obliczyć procent danej liczby, jak obliczyć, ile procent jednej liczby stanowi druga liczba, oraz jak obliczyć liczbę, znając jej procent.

Procent danej liczby: x% z A = (x/100) * A
Jaki procent A stanowi B: (B/A) * 100%
Obliczanie liczby, gdy znamy jej procent: Jeśli x% z A = B, to A = B / (x/100)

Pamiętaj o punktach procentowych – to różnica między dwoma wartościami wyrażonymi w procentach. Np. wzrost z 10% do 15% to wzrost o 5 punktów procentowych.

Algebra

Wzory skróconego mnożenia

To niezbędne wzory, które musisz znać na pamięć. Ułatwiają rozwiązywanie wielu zadań!

(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
(a + b)(a - b) = a² - b²

Ćwicz ich stosowanie, rozwiązując zadania z podręcznika i arkuszy egzaminacyjnych.

Równania i nierówności

Musisz umieć rozwiązywać równania liniowe z jedną niewiadomą oraz nierówności liniowe z jedną niewiadomą. Pamiętaj o przenoszeniu wyrazów na drugą stronę równania/nierówności (ze zmianą znaku) i redukcji wyrazów podobnych.

Układy równań

Dwa sposoby rozwiązywania układów równań:

Metoda podstawiania: Wyznaczasz jedną niewiadomą z jednego równania i podstawiasz ją do drugiego.
Metoda przeciwnych współczynników: Mnożysz jedno lub oba równania przez taką liczbę, aby przy jednej z niewiadomych otrzymać przeciwne współczynniki. Następnie dodajesz równania stronami.

Wybierz metodę, która w danym przypadku jest najprostsza.

Geometria

Figury płaskie

Trójkąt:

Pole: P = 1/2 * a * h (gdzie a to podstawa, h to wysokość opuszczona na tę podstawę)

Szczególne przypadki:

Trójkąt równoboczny: P = (a²√3)/4, h = (a√3)/2
Twierdzenie Pitagorasa (dla trójkąta prostokątnego): a² + b² = c² (gdzie a i b to przyprostokątne, c to przeciwprostokątna)

Kwadrat:

Pole: P = a²
Obwód: O = 4a

Prostokąt:

Pole: P = a * b
Obwód: O = 2a + 2b

Równoległobok:

Pole: P = a * h (gdzie a to podstawa, h to wysokość opuszczona na tę podstawę)

Romb:

Pole: P = a * h lub P = 1/2 * d₁ * d₂ (gdzie d₁ i d₂ to przekątne)

Trapez:

Pole: P = 1/2 * (a + b) * h (gdzie a i b to podstawy, h to wysokość)

Koło i okrąg:

Pole koła: P = πr² (gdzie r to promień)
Obwód okręgu (długość okręgu): O = 2πr lub O = πd (gdzie d to średnica)

Figury przestrzenne

Prostopadłościan:

Objętość: V = a * b * c (gdzie a, b, c to długości krawędzi)

Sześcian:

Objętość: V = a³ (gdzie a to długość krawędzi)

Graniastosłup prosty:

Objętość: V = P_p * H (gdzie P_p to pole podstawy, H to wysokość graniastosłupa)

Walec:

Objętość: V = πr² * H (gdzie r to promień podstawy, H to wysokość walca)

Ostrosłup:

Objętość: V = 1/3 * P_p * H (gdzie P_p to pole podstawy, H to wysokość ostrosłupa)

Stożek:

Objętość: V = 1/3 * πr² * H (gdzie r to promień podstawy, H to wysokość stożka)

Kula:

Objętość: V = 4/3 * πr³ (gdzie r to promień kuli)

Własności figur

Musisz znać własności figur płaskich i przestrzennych. Wiedzieć, jakie są rodzaje trójkątów, czworokątów, graniastosłupów, ostrosłupów. Jakie są ich cechy charakterystyczne? Jakie relacje zachodzą między ich bokami, kątami, wysokościami, etc.

Inne przydatne informacje

Jednostki miar

Pamiętaj o przeliczaniu jednostek! Długość (mm, cm, dm, m, km), pole (mm², cm², dm², m², km²), objętość (mm³, cm³, dm³, m³), masa (g, dag, kg, t), czas (s, min, h, dzień).

Prędkość, droga, czas

v = s/t (prędkość = droga / czas)
s = v * t (droga = prędkość * czas)
t = s/v (czas = droga / prędkość)

Pamiętaj o jednostkach! Jeśli prędkość jest w km/h, to droga musi być w km, a czas w godzinach.

Statystyka

Średnia arytmetyczna: Suma wszystkich wartości podzielona przez liczbę wartości.
Mediana: Wartość środkowa w uporządkowanym zbiorze danych (jeśli liczba danych jest parzysta, to mediana jest średnią arytmetyczną dwóch środkowych wartości).
Dominanta: Wartość, która występuje najczęściej w zbiorze danych.

Rachunek prawdopodobieństwa

Prawdopodobieństwo zdarzenia A: P(A) = (liczba sprzyjających zdarzeń) / (liczba wszystkich możliwych zdarzeń).

Podsumowanie

To wszystkie wzory, które musisz znać na egzamin ósmoklasisty z matematyki w 2022 roku. Kluczem do sukcesu jest nie tylko ich znajomość, ale przede wszystkim umiejętność zastosowania ich w zadaniach. Dlatego rozwiązuj jak najwięcej zadań, analizuj błędy i nie bój się prosić o pomoc, jeśli czegoś nie rozumiesz. Powodzenia na egzaminie!