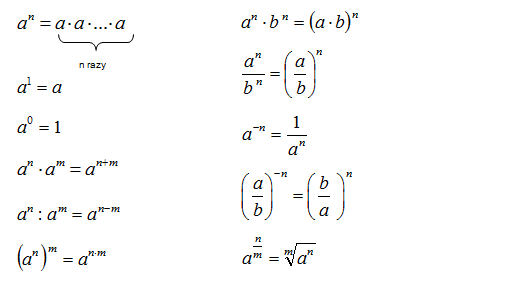Wzory Na Działania Na Potęgach

Czy kiedykolwiek patrzyłeś na wyrażenie z potęgami i czułeś się przytłoczony? Nie jesteś sam! Potęgi, choć wydają się skomplikowane, kryją w sobie logiczny porządek i, co najważniejsze, **zestaw konkretnych wzorów**, które znacząco ułatwiają obliczenia. Zrozumienie tych wzorów to klucz do opanowania potęg i sprawnego rozwiązywania zadań matematycznych. Przejdźmy więc razem przez te wzory, krok po kroku, abyś mógł wreszcie poczuć się pewnie i komfortowo.
Podstawowe Wzory Na Działania Na Potęgach
Zacznijmy od fundamentów. Te wzory są esencją działań na potęgach i warto je zapamiętać na początku.
1. Mnożenie Potęg o Tej Samej Podstawie
Wyobraź sobie, że masz do pomnożenia dwa wyrażenia potęgowe, które mają identyczną podstawę. To oznacza, że liczba, która jest podnoszona do potęgi, jest taka sama w obu wyrażeniach. Wtedy możesz skorzystać z prostego wzoru:
am * an = am+n
Co to znaczy? Mówiąc prościej, aby pomnożyć potęgi o tej samej podstawie, wystarczy zsumować ich wykładniki i zapisać wynik z tą samą podstawą. Na przykład:
23 * 22 = 23+2 = 25 = 32
Jak to działa w praktyce? Pomyśl o tym tak: 23 to 2*2*2, a 22 to 2*2. Mnożąc je razem, otrzymujemy 2*2*2*2*2, co jest równe 25.
2. Dzielenie Potęg o Tej Samej Podstawie
Analogicznie do mnożenia, istnieje wzór na dzielenie potęg o tej samej podstawie:
am / an = am-n (gdzie a ≠ 0)
Tutaj, aby podzielić potęgi o tej samej podstawie, odejmujemy wykładnik dzielnika od wykładnika dzielnej. Pamiętaj, że podstawa 'a' nie może być równa zero, ponieważ dzielenie przez zero jest niedozwolone.
Przykład:
54 / 52 = 54-2 = 52 = 25
Dlaczego tak się dzieje? 54 to 5*5*5*5, a 52 to 5*5. Dzieląc je, "skracamy" dwa 5 z licznika i mianownika, pozostawiając 5*5, czyli 52.
3. Potęga Potęgi
Ten wzór dotyczy sytuacji, w której potęga jest podnoszona do innej potęgi:
(am)n = am*n
W tym przypadku, aby obliczyć wartość wyrażenia, mnożymy wykładniki.
Przykład:
(32)3 = 32*3 = 36 = 729
Spójrzmy na to: (32)3 oznacza, że 32 (czyli 9) jest podnoszone do potęgi 3, czyli mnożymy 9 przez siebie trzy razy: 9 * 9 * 9. Zamiast tego, możemy od razu pomnożyć wykładniki (2 i 3), co daje nam 36, czyli 3 * 3 * 3 * 3 * 3 * 3 = 729.
4. Potęga Iloczynu
Kiedy mamy iloczyn kilku liczb podniesiony do potęgi, możemy rozbić potęgę na każdy czynnik iloczynu:
(a * b)n = an * bn
Każdy czynnik w nawiasie podnosimy do potęgi.
Przykład:
(2 * 3)2 = 22 * 32 = 4 * 9 = 36
To dlatego, że (2*3)2 = 62 = 36. A również 22 * 32 = 4 * 9 = 36. Otrzymujemy ten sam wynik!
5. Potęga Ilorazu
Podobnie jak w przypadku iloczynu, możemy rozbić potęgę na licznik i mianownik ilorazu:
(a / b)n = an / bn (gdzie b ≠ 0)
Licznik i mianownik ułamka podnosimy do potęgi. Pamiętaj, że mianownik 'b' nie może być równy zero.
Przykład:
(4 / 2)3 = 43 / 23 = 64 / 8 = 8
Ponieważ (4/2)3 = 23 = 8, a 43 / 23 = 64 / 8 = 8, widzimy, że wzór działa.
Potęga o Wykładniku Zerowym i Ujemnym
Oprócz podstawowych wzorów, warto pamiętać o potęgach o wykładnikach zerowych i ujemnych.
1. Potęga o Wykładniku Zerowym
a0 = 1 (gdzie a ≠ 0)
Dowolna liczba (różna od zera) podniesiona do potęgi zerowej daje w wyniku 1. Jest to fundamentalna zasada w matematyce. Wyjątkiem jest 00, które jest wyrażeniem nieokreślonym.
Przykład:
70 = 1
(-5)0 = 1
2. Potęga o Wykładniku Ujemnym
a-n = 1 / an (gdzie a ≠ 0)
Liczba podniesiona do potęgi ujemnej jest równa odwrotności tej liczby podniesionej do potęgi o wartości bezwzględnej tego wykładnika. Innymi słowy, potęga ujemna oznacza odwrotność potęgi o wykładniku dodatnim.
Przykład:
2-3 = 1 / 23 = 1 / 8
Dzięki temu wzorowi, potęgi ujemne stają się łatwiejsze do zrozumienia i obliczenia.
Praktyczne Zastosowanie Wzorów
Znajomość wzorów na działania na potęgach jest niezwykle przydatna w wielu dziedzinach, nie tylko w matematyce szkolnej. Przykładowo:
- Informatyka: Obliczenia związane z pojemnością pamięci komputerowej (np. 210 bajtów = 1 kilobajt).
- Finanse: Obliczanie procentu składanego (np. wartość inwestycji po n latach).
- Fizyka: Opisywanie zjawisk fizycznych, takich jak natężenie światła (zależność kwadratowa od odległości).
- Chemia: Określanie stężeń roztworów.
Spójrzmy na prosty przykład związany z informatyką. Często słyszymy o megabajtach (MB) i gigabajtach (GB). Wiemy, że 1 GB to więcej niż 1 MB. Ale ile dokładnie? Otóż, 1 MB to 220 bajtów, a 1 GB to 230 bajtów. Stosując wzór na dzielenie potęg o tej samej podstawie, możemy obliczyć, ile razy GB jest większy od MB: 230 / 220 = 230-20 = 210 = 1024. Zatem 1 GB to 1024 MB.
Wskazówki i Triki
Oto kilka wskazówek, które pomogą Ci w efektywnym korzystaniu ze wzorów na działania na potęgach:
- Zapamiętaj wzory: Regularne powtarzanie i rozwiązywanie zadań to najlepszy sposób na utrwalenie wzorów.
- Uprość wyrażenie: Zanim zaczniesz obliczenia, postaraj się uprościć wyrażenie, stosując odpowiednie wzory.
- Zwróć uwagę na kolejność działań: Pamiętaj o kolejności wykonywania działań (potęgowanie, mnożenie/dzielenie, dodawanie/odejmowanie).
- Sprawdzaj wyniki: Zawsze warto sprawdzić wynik, szczególnie w bardziej skomplikowanych zadaniach.
- Ćwicz, ćwicz i jeszcze raz ćwicz: Rozwiązuj różnorodne zadania, aby nabrać wprawy w stosowaniu wzorów.
Podsumowanie
Wzory na działania na potęgach są niezbędnym narzędziem w matematyce. Zrozumienie i opanowanie tych wzorów otwiera drzwi do rozwiązywania wielu problemów matematycznych i praktycznych. Nie zrażaj się początkowymi trudnościami. Z regularną praktyką i odrobiną cierpliwości, staniesz się mistrzem potęg!
Pamiętaj, że kluczem do sukcesu jest zrozumienie, dlaczego wzory działają, a nie tylko ich bezmyślne zapamiętywanie. Staraj się analizować przykłady i rozwiązywać zadania samodzielnie. W ten sposób zdobędziesz prawdziwą wiedzę i umiejętności, które przydadzą Ci się w przyszłości.