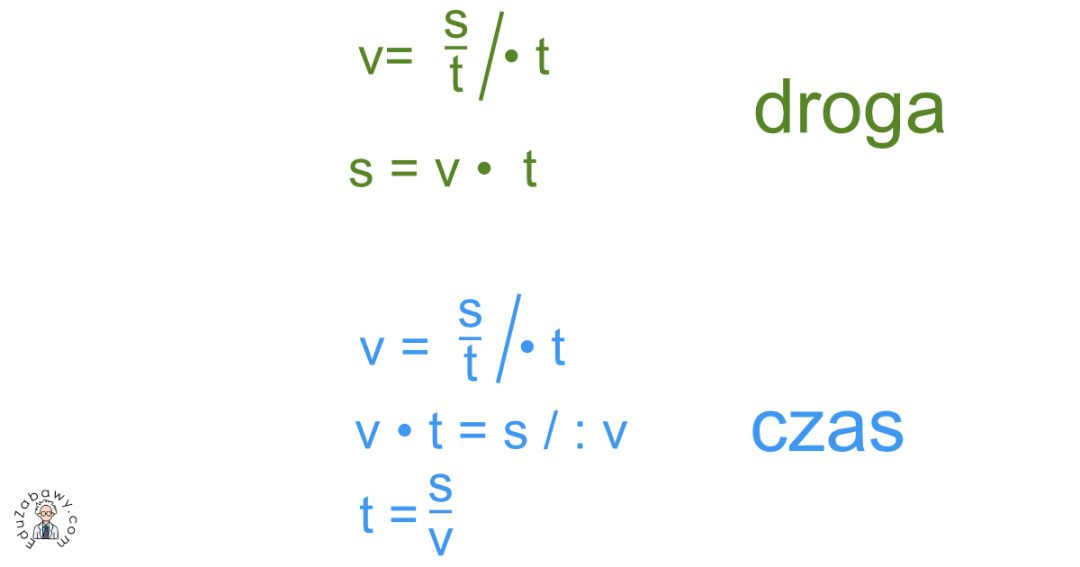Wzory Na Czas Droge I Predkosc

Rozumienie zależności między czasem, drogą i prędkością jest fundamentalne nie tylko w fizyce, ale i w codziennym życiu. Czy to planowanie podróży, analizowanie wyników sportowych, czy nawet gotowanie – zasady te są wszechobecne. Ten artykuł ma na celu szczegółowe wyjaśnienie wzorów opisujących te wielkości, ich wzajemnych relacji i praktycznego zastosowania.

Podstawowe wzory: Fundament zrozumienia ruchu

Zacznijmy od definicji podstawowych wielkości:

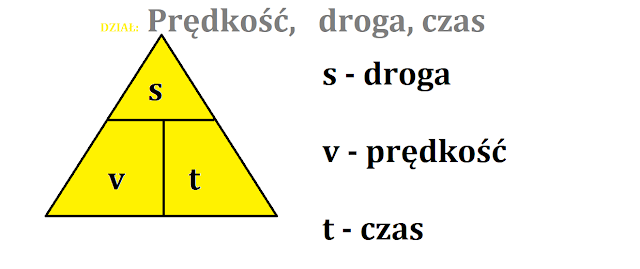
Droga (s): Całkowita długość pokonana przez obiekt w ruchu. Mierzymy ją najczęściej w metrach (m) lub kilometrach (km).
Czas (t): Okres, w którym odbywa się ruch. Mierzymy go w sekundach (s), minutach (min) lub godzinach (h).
Prędkość (v): Szybkość zmiany położenia obiektu w czasie. Mierzymy ją w metrach na sekundę (m/s) lub kilometrach na godzinę (km/h).

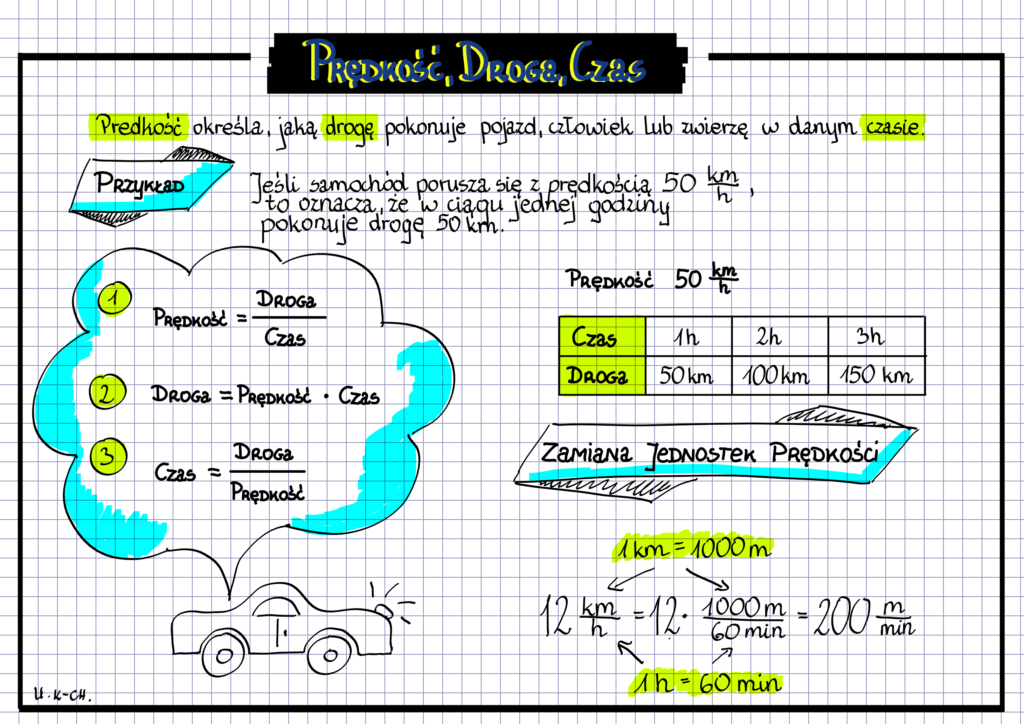
Podstawowy wzór łączący te wielkości to:

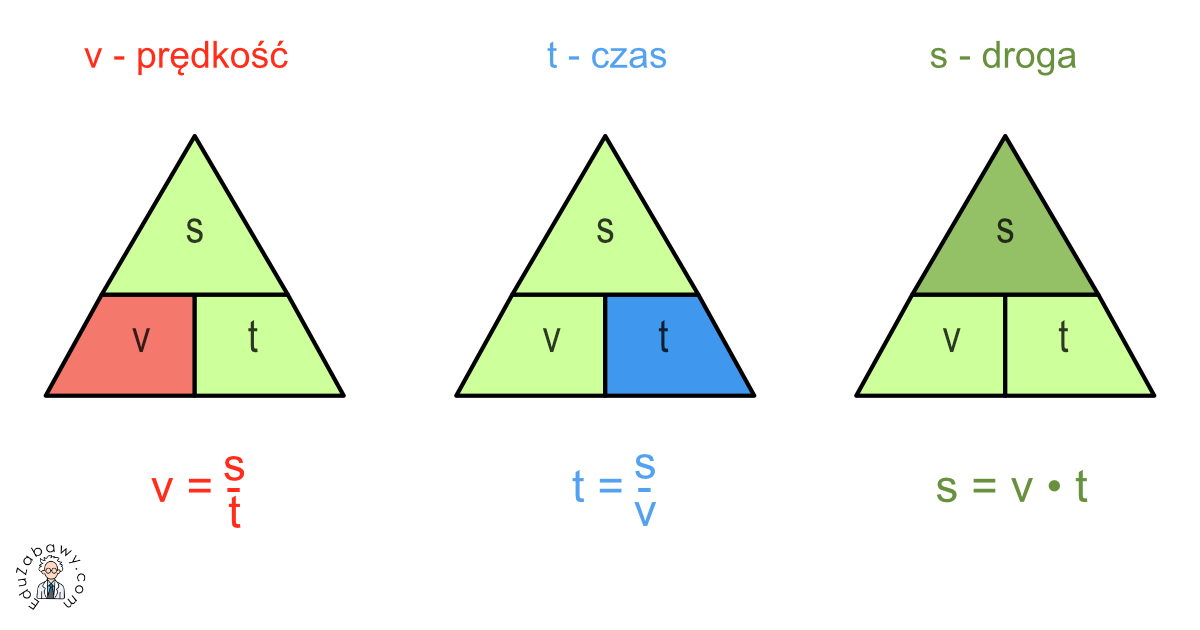
v = s / t

Co oznacza: Prędkość jest równa drodze podzielonej przez czas.

Przekształcanie wzorów

Z powyższego wzoru możemy wyprowadzić pozostałe:

s = v * t (Droga równa się prędkości pomnożonej przez czas)
t = s / v (Czas równa się drodze podzielonej przez prędkość)

Kluczem jest zrozumienie, że wzory te dotyczą ruchu jednostajnego prostoliniowego, czyli ruchu, w którym prędkość obiektu jest stała i porusza się on po linii prostej. W bardziej złożonych przypadkach, gdy prędkość się zmienia, sytuacja staje się bardziej skomplikowana i wymaga zastosowania innych metod, takich jak rachunek różniczkowy i całkowy.

Jednostki miar i ich konwersja

Niezwykle istotne jest zwracanie uwagi na jednostki miar. Częstym błędem jest mieszanie jednostek, np. używanie kilometrów do drogi i sekund do czasu, co prowadzi do błędnych obliczeń prędkości. Trzeba pamiętać o konwersji jednostek.

Przykłady konwersji:

km/h na m/s: Pomnóż prędkość w km/h przez 1000/3600 (lub podziel przez 3.6). Na przykład, 72 km/h = 72 * (1000/3600) m/s = 20 m/s.
m/s na km/h: Pomnóż prędkość w m/s przez 3.6. Na przykład, 25 m/s = 25 * 3.6 km/h = 90 km/h.

Podobnie, konwersja jednostek czasu:

Godziny na minuty: Pomnóż liczbę godzin przez 60.
Minuty na sekundy: Pomnóż liczbę minut przez 60.

Przykłady zastosowań w życiu codziennym

Poniżej przedstawione są przykłady, jak wzory na prędkość, drogę i czas znajdują zastosowanie w praktyce.

Planowanie podróży

Wyobraź sobie, że planujesz podróż samochodem z Warszawy do Krakowa, odległość między miastami wynosi około 300 km. Chcesz wiedzieć, ile czasu zajmie Ci podróż, zakładając średnią prędkość 100 km/h.

Używamy wzoru: t = s / v

Podstawiamy wartości: t = 300 km / 100 km/h = 3 h

Oznacza to, że podróż powinna zająć około 3 godzin, pomijając przerwy i utrudnienia na drodze.

Analiza wyników sportowych

Sprinter przebiegł dystans 100 metrów w czasie 10 sekund. Oblicz jego średnią prędkość.

Używamy wzoru: v = s / t

Podstawiamy wartości: v = 100 m / 10 s = 10 m/s

Średnia prędkość sprintera wynosiła 10 m/s. Możemy to przeliczyć na km/h: 10 m/s * 3.6 = 36 km/h.

Gotowanie

Chcesz upiec ciasto, które wymaga pieczenia w piekarniku przez 45 minut w temperaturze 180 stopni Celsjusza. Chociaż nie jest to bezpośrednio związane z ruchem, koncepcja czasu odgrywa kluczową rolę. Musisz precyzyjnie odmierzyć czas, aby ciasto się udało.

Ruch jednostajny prostoliniowy a ruch zmienny

Wcześniej wspomniano o ruchu jednostajnym prostoliniowym. Jednak w rzeczywistości większość ruchów jest zmienna, czyli prędkość obiektu ulega zmianie w czasie. W takich przypadkach używamy pojęcia przyspieszenia (a), które określa, jak szybko zmienia się prędkość.

Wzory dla ruchu jednostajnie przyspieszonego (gdzie przyspieszenie jest stałe):

v = v₀ + at (Prędkość końcowa równa się prędkości początkowej plus przyspieszenie razy czas)
s = v₀t + (1/2)at² (Droga równa się prędkości początkowej razy czas plus połowa przyspieszenia razy czas do kwadratu)

Gdzie:

v₀ - prędkość początkowa
a - przyspieszenie

Przykład: Samochód rusza z miejsca (v₀ = 0 m/s) i przyspiesza z przyspieszeniem 2 m/s² przez 5 sekund. Jaką prędkość osiągnie i jaką drogę pokona?

Prędkość: v = 0 + 2 * 5 = 10 m/s

Droga: s = 0 * 5 + (1/2) * 2 * 5² = 25 m

Samochód osiągnie prędkość 10 m/s i pokona drogę 25 metrów.

Błędy pomiarowe i niepewności

W praktycznych pomiarach zawsze występują błędy i niepewności. Oznacza to, że uzyskane wartości drogi, czasu i prędkości są obarczone pewną nieprecyzją. Ważne jest, aby zdawać sobie z tego sprawę i uwzględniać to w analizie wyników.

Źródła błędów mogą być różne:

Niedokładność przyrządów pomiarowych: Każdy przyrząd ma określoną dokładność.
Błędy systematyczne: Wynikające z wadliwego działania przyrządu lub metody pomiarowej.
Błędy losowe: Wynikające z przypadkowych czynników, takich jak warunki atmosferyczne czy subiektywna ocena osoby dokonującej pomiaru.

W celu minimalizacji błędów, należy stosować odpowiednie metody pomiarowe, używać dokładnych przyrządów i powtarzać pomiary wielokrotnie, obliczając średnią wartość oraz niepewność pomiarową.

Zaawansowane koncepcje: Ruch w dwóch i trzech wymiarach

W rzeczywistości ruch rzadko odbywa się po linii prostej. Obiekty poruszają się w dwóch (np. ruch po powierzchni) lub trzech (np. lot samolotu) wymiarach. W takim przypadku musimy rozpatrywać wektory prędkości i przyspieszenia, a także używać bardziej zaawansowanych narzędzi matematycznych, takich jak geometria analityczna i rachunek wektorowy.

Przykład: Rzut ukośny (np. rzut piłką). Tor ruchu piłki jest parabolą, a jej prędkość zmienia się zarówno w kierunku poziomym, jak i pionowym. Analiza takiego ruchu wymaga rozłożenia prędkości na składowe i zastosowania praw fizyki oddzielnie dla każdego kierunku.

Podsumowanie i wnioski

Zrozumienie wzorów na czas, drogę i prędkość jest niezbędne do analizy i przewidywania ruchu obiektów. Od planowania podróży, przez analizę wyników sportowych, po zaawansowane obliczenia inżynieryjne – zasady te są uniwersalne i znajdują zastosowanie w wielu dziedzinach. Pamiętaj o poprawnym używaniu jednostek miar oraz uwzględnianiu błędów pomiarowych.

Zachęcam do dalszego zgłębiania wiedzy z zakresu fizyki ruchu, aby jeszcze lepiej zrozumieć otaczający nas świat. Spróbuj analizować ruch różnych obiektów w swoim otoczeniu i obliczać ich prędkość, drogę i czas. To najlepszy sposób na utrwalenie wiedzy i rozwinięcie umiejętności praktycznych.