Wzory Matematyczne Na Egzamin ósmoklasisty

Zbliża się egzamin ósmoklasisty z matematyki? Stresujesz się ilością wzorów, które musisz zapamiętać? Spokojnie! Ten artykuł jest właśnie dla Ciebie. Przygotowaliśmy kompendium wiedzy, które pomoże Ci usystematyzować i utrwalić niezbędne wzory matematyczne, tak abyś na egzaminie czuł się pewnie i mógł skupić się na rozwiązywaniu zadań.

Naszym celem jest przekazanie wiedzy w sposób przystępny i zrozumiały dla każdego ucznia ósmej klasy. Pominiemy zbędne skomplikowania i skupimy się na praktycznym zastosowaniu wzorów. Razem przejdziemy przez najważniejsze zagadnienia, aby żaden wzór Cię nie zaskoczył.

Podstawowe Działania i Własności Liczb

Fundamentem matematyki są oczywiście działania na liczbach. Zanim przejdziemy do bardziej zaawansowanych zagadnień, przypomnijmy sobie kilka podstawowych zasad:

Kolejność wykonywania działań: Pamiętaj o kolejności: nawiasy, potęgowanie/pierwiastkowanie, mnożenie/dzielenie, dodawanie/odejmowanie. Popularny akronim: PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).
Działania na ułamkach:
- Dodawanie/odejmowanie: sprowadzenie do wspólnego mianownika.
- Mnożenie: licznik razy licznik, mianownik razy mianownik.
- Dzielenie: mnożenie przez odwrotność dzielnika.
Działania na liczbach dodatnich i ujemnych: Zwróć uwagę na znaki! Pamiętaj o zasadach: minus razy minus daje plus, plus razy minus daje minus.

Warto także pamiętać o własnościach działań, takich jak łączność i przemienność dodawania i mnożenia.

Potęgi i Pierwiastki

Potęgi i pierwiastki to zagadnienie, które często sprawia problemy. Zobaczmy, jak je ogarnąć:

Wzory na potęgi:

aⁿ = a * a * ... * a (n razy) – podstawowa definicja potęgi.
a⁰ = 1 – każda liczba podniesiona do potęgi zerowej daje 1 (z wyjątkiem 0⁰, które jest nieokreślone).
a¹ = a – każda liczba podniesiona do potęgi pierwszej daje tę samą liczbę.
a^-n = 1 / aⁿ – potęga ujemna to odwrotność potęgi dodatniej.
a^m * aⁿ = a^m+n – mnożenie potęg o tej samej podstawie.
a^m / aⁿ = a^m-n – dzielenie potęg o tej samej podstawie.
(a^m)ⁿ = a^m*n – potęgowanie potęgi.
(a * b)ⁿ = aⁿ * bⁿ – potęgowanie iloczynu.
(a / b)ⁿ = aⁿ / bⁿ – potęgowanie ilorazu.

Wzory na pierwiastki:

√a – pierwiastek kwadratowy z liczby a.
∛a – pierwiastek sześcienny z liczby a.
√(a * b) = √a * √b – pierwiastek z iloczynu.
√(a / b) = √a / √b – pierwiastek z ilorazu.
√(a²) = |a| – pierwiastek kwadratowy z kwadratu liczby. Pamiętaj o wartości bezwzględnej!

Ćwicz regularnie na przykładach, aby te wzory stały się dla Ciebie intuicyjne.

Wyrażenia Algebraiczne

Wyrażenia algebraiczne to kombinacje liczb, liter (reprezentujących zmienne) i znaków działań. Kluczowe jest umiejętne operowanie nimi:

Redukcja wyrazów podobnych: Łączymy wyrazy, które mają te same zmienne w tych samych potęgach.
Mnożenie sum algebraicznych: Każdy wyraz z pierwszego nawiasu mnożymy przez każdy wyraz z drugiego nawiasu.
Wzory skróconego mnożenia:
- (a + b)² = a² + 2ab + b² – kwadrat sumy.
- (a - b)² = a² - 2ab + b² – kwadrat różnicy.
- (a + b)(a - b) = a² - b² – różnica kwadratów.

Wzory skróconego mnożenia znacznie ułatwiają rozwiązywanie zadań, więc warto je zapamiętać i nauczyć się rozpoznawać sytuacje, w których można je zastosować.

Równania i Nierówności

Rozwiązywanie równań i nierówności to kolejna kluczowa umiejętność:

Równania liniowe: Przenosimy niewiadome na jedną stronę, liczby na drugą, a następnie dzielimy przez współczynnik przy niewiadomej.
Nierówności liniowe: Rozwiązujemy podobnie jak równania, ale pamiętamy o zmianie znaku nierówności przy mnożeniu lub dzieleniu przez liczbę ujemną.
Układy równań: Możemy je rozwiązać metodą podstawiania lub metodą przeciwnych współczynników.

Pamiętaj o sprawdzaniu rozwiązań równań i nierówności, aby upewnić się, że nie popełniłeś błędu.

Geometria

Geometria to obszerny dział, który wymaga znajomości wielu wzorów. Przyjrzyjmy się najważniejszym:

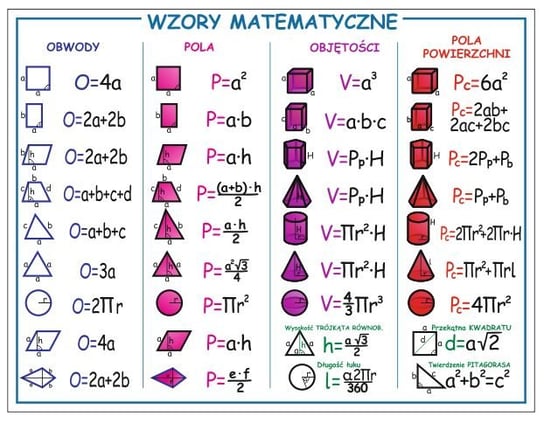
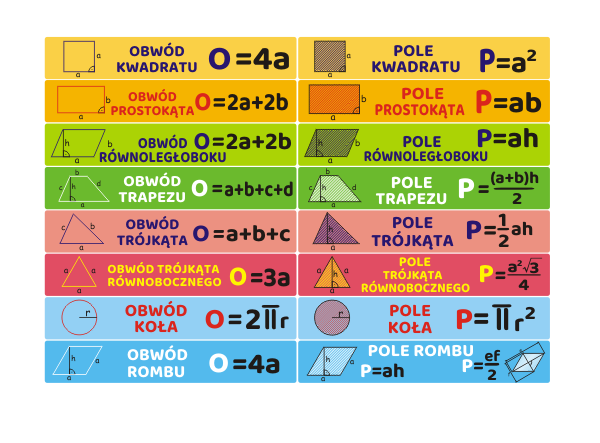
Figury płaskie:

Kwadrat:
- Pole: P = a²
- Obwód: O = 4a
Prostokąt:
- Pole: P = a * b
- Obwód: O = 2a + 2b
Trójkąt:
- Pole: P = (a * h) / 2
- Obwód: O = a + b + c
Równoległobok:
- Pole: P = a * h
- Obwód: O = 2a + 2b
Romb:
- Pole: P = (e * f) / 2 (gdzie e i f to przekątne)
- Obwód: O = 4a
Trapez:
- Pole: P = ((a + b) * h) / 2
Koło:
- Pole: P = πr²
- Obwód (długość okręgu): O = 2πr

Bryły:

Prostopadłościan:
- Objętość: V = a * b * c
- Pole powierzchni: P = 2(ab + ac + bc)
Sześcian:
- Objętość: V = a³
- Pole powierzchni: P = 6a²
Graniastosłup:
- Objętość: V = P_podstawy * H
Walec:
- Objętość: V = πr²H
- Pole powierzchni: P = 2πr² + 2πrH
Stożek:
- Objętość: V = (1/3)πr²H
Kula:
- Objętość: V = (4/3)πr³
- Pole powierzchni: P = 4πr²

Pamiętaj o jednostkach! Pole powierzchni wyrażamy w jednostkach kwadratowych, a objętość w jednostkach sześciennych.

Procenty

Procenty pojawiają się w wielu zadaniach, dlatego warto je dobrze zrozumieć:

Obliczanie procentu danej liczby: Mnożymy daną liczbę przez procent (zamieniony na ułamek dziesiętny).
Obliczanie liczby, gdy dany jest jej procent: Dzielimy znaną wartość procentową przez odpowiadający jej procent (zamieniony na ułamek dziesiętny).
Obliczanie, jakim procentem jednej liczby jest druga liczba: Dzielimy jedną liczbę przez drugą i mnożymy przez 100%.
Zmiana procentowa: ((wartość końcowa - wartość początkowa) / wartość początkowa) * 100%

Zwróć uwagę na sformułowania "o ile procent więcej" i "o ile procent mniej".

Rachunek Prawdopodobieństwa

Rachunek prawdopodobieństwa pozwala oszacować szanse na wystąpienie danego zdarzenia:

Prawdopodobieństwo zdarzenia: P(A) = (liczba sprzyjających zdarzeń) / (liczba wszystkich możliwych zdarzeń)

Pamiętaj, że prawdopodobieństwo zawsze jest liczbą z przedziału [0, 1].

Układ Współrzędnych

Układ współrzędnych pozwala opisywać położenie punktów na płaszczyźnie:

Współrzędne punktu: Para liczb (x, y), gdzie x to odcięta, a y to rzędna.
Odległość między dwoma punktami: √((x₂ - x₁)² + (y₂ - y₁)²)

Zrozumienie układu współrzędnych jest kluczowe do rozwiązywania zadań związanych z geometrią analityczną.

Wskazówki i Triki

Oprócz znajomości wzorów, warto pamiętać o kilku wskazówkach, które mogą Ci pomóc na egzaminie:

Czytaj uważnie polecenia: Zwróć uwagę na szczegóły, takie jak jednostki miar i sformułowania pytania.
Wykonuj rysunki pomocnicze: Często rysunek pomaga zrozumieć treść zadania i znaleźć rozwiązanie.
Sprawdzaj swoje odpowiedzi: Jeśli masz czas, sprawdź, czy Twoja odpowiedź ma sens i czy spełnia warunki zadania.
Nie panikuj: Jeśli nie wiesz, jak rozwiązać jakieś zadanie, przejdź do następnego. Możesz do niego wrócić później.
Używaj brudnopisu: Nie wstydź się korzystać z brudnopisu do wykonywania obliczeń i szkiców.

Pamiętaj, że sukces na egzaminie ósmoklasisty to połączenie wiedzy, umiejętności i pewności siebie. Im więcej ćwiczysz, tym bardziej czujesz się komfortowo z materiałem. Nie odkładaj nauki na ostatnią chwilę, rozłóż ją na mniejsze partie i regularnie powtarzaj materiał.

Wierzymy w Ciebie! Powodzenia na egzaminie!