Wzor Na Wysokosc Ostroslupa
Witajcie! Dziś zajmiemy się bardzo ważnym zagadnieniem w geometrii przestrzennej – wysokością ostrosłupa. Zrozumienie, czym jest wysokość ostrosłupa i jak ją obliczyć, jest kluczowe do rozwiązywania zadań z geometrii, obliczania objętości i powierzchni ostrosłupów, a także do wizualizacji przestrzennej.
Czym jest ostrosłup?
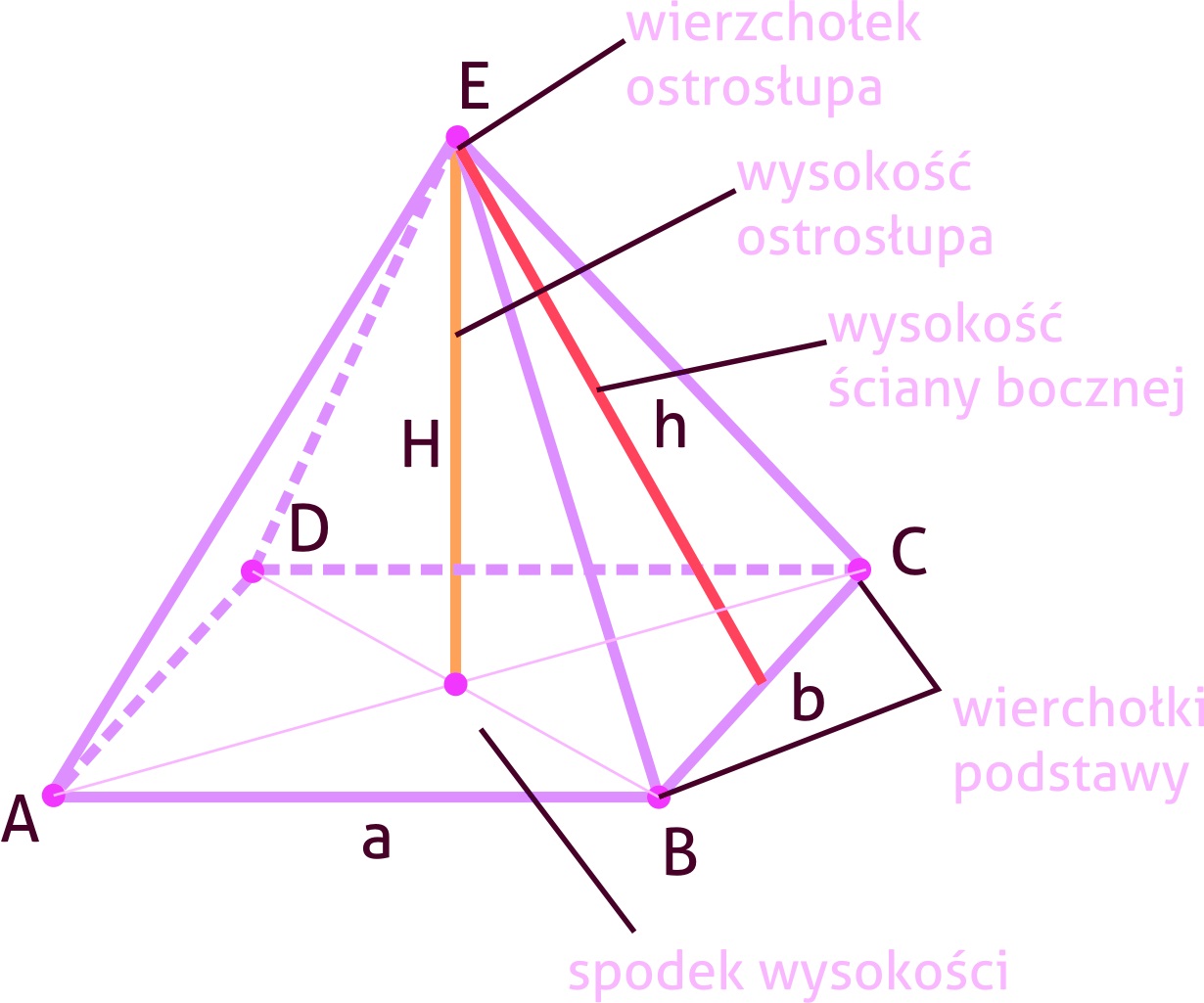
Zanim przejdziemy do wzoru na wysokość, musimy przypomnieć sobie, czym w ogóle jest ostrosłup. Otóż, ostrosłup to wielościan, którego jedna ściana (zwana podstawą) jest dowolnym wielokątem, a pozostałe ściany (zwane ścianami bocznymi) są trójkątami, mającymi wspólny wierzchołek (zwany wierzchołkiem ostrosłupa). Przykładami ostrosłupów są ostrosłupy trójkątne (czworościany), ostrosłupy czworokątne (np. piramidy) i ostrosłupy o podstawie wielokąta o większej liczbie boków.
Ważne jest, aby odróżnić ostrosłup prosty od ostrosłupa pochyłego. W ostrosłupie prostym, spodek wysokości (czyli punkt, w którym wysokość ostrosłupa styka się z podstawą) pokrywa się ze środkiem okręgu opisanego na podstawie (lub, w przypadku ostrosłupa prawidłowego, ze środkiem podstawy). W ostrosłupie pochyłym, spodek wysokości leży poza tym środkiem.
Czym jest wysokość ostrosłupa?
Wysokość ostrosłupa to odcinek prostopadły poprowadzony z wierzchołka ostrosłupa do płaszczyzny podstawy. Długość tego odcinka nazywamy także wysokością ostrosłupa i oznaczamy zazwyczaj literą H (duże "ha").
Wyobraźmy sobie, że trzymamy ostrosłup w powietrzu. Wysokość to po prostu odległość od najwyższego punktu ostrosłupa (wierzchołka) do poziomu podłogi (podstawy).
Wzory na wysokość ostrosłupa
Obliczanie wysokości ostrosłupa zależy od tego, jakie informacje posiadamy. Najczęściej stosuje się następujące metody:
1. Wykorzystanie twierdzenia Pitagorasa
Jeżeli znamy długość krawędzi bocznej ostrosłupa (b) oraz odległość spodka wysokości od wierzchołka podstawy (r) (np. promień okręgu opisanego na podstawie w przypadku ostrosłupa prawidłowego), to możemy zastosować twierdzenie Pitagorasa:
H2 + r2 = b2
Zatem:
H = √(b2 - r2)
Przykład: Mamy ostrosłup prawidłowy czworokątny o krawędzi bocznej długości 13 cm. Spodek wysokości znajduje się w środku kwadratu będącego podstawą, a odległość tego środka od wierzchołka kwadratu (r) wynosi 5 cm. Zatem wysokość ostrosłupa:
H = √(132 - 52) = √(169 - 25) = √144 = 12 cm
2. Wykorzystanie trygonometrii
Jeśli znamy długość krawędzi bocznej (b) i kąt (α) między krawędzią boczną a płaszczyzną podstawy, możemy użyć funkcji trygonometrycznej sinusa:
sin(α) = H / b
Zatem:
H = b * sin(α)
Przykład: Mamy ostrosłup o krawędzi bocznej długości 8 cm. Kąt między krawędzią boczną a płaszczyzną podstawy wynosi 60 stopni. Zatem wysokość ostrosłupa:
H = 8 * sin(60°) = 8 * (√3 / 2) = 4√3 cm
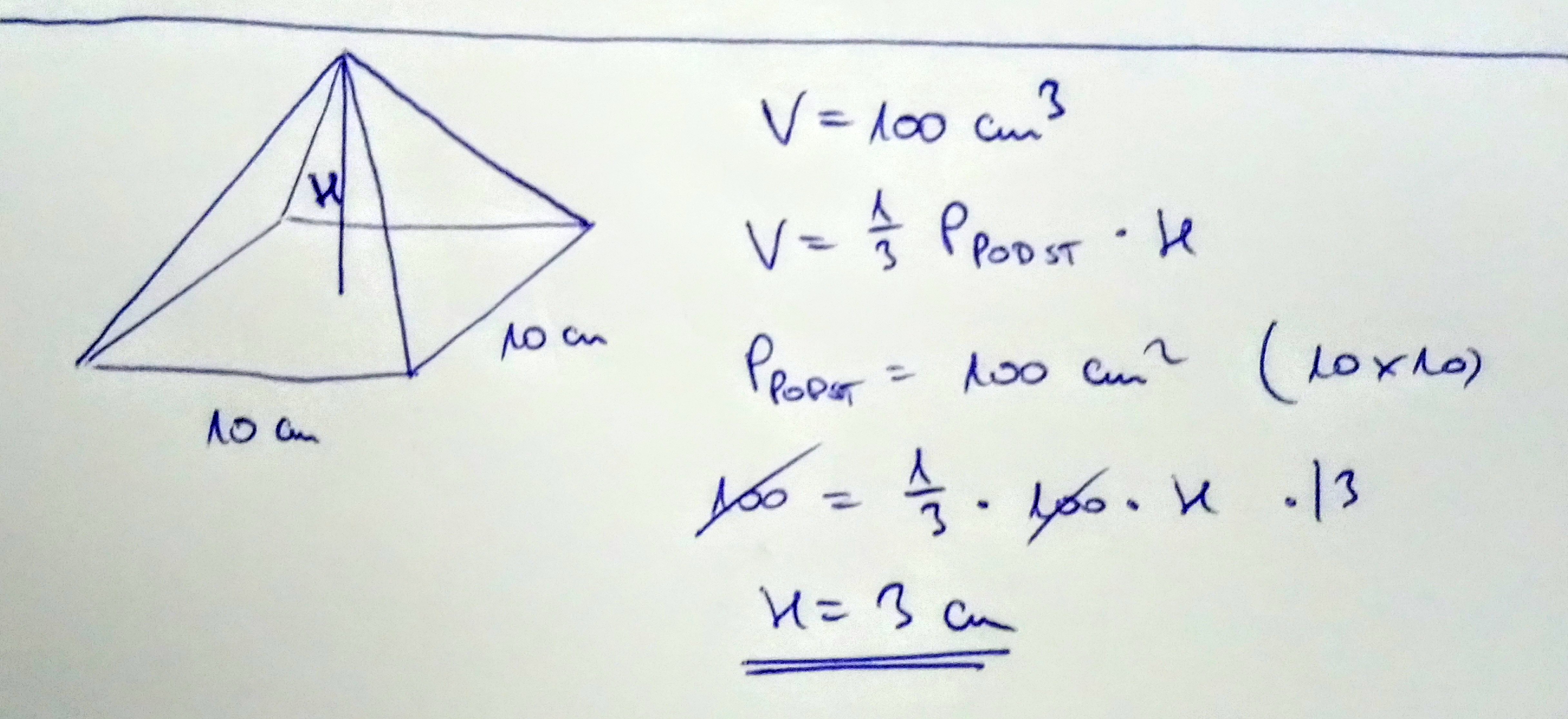
3. Wykorzystanie objętości i pola podstawy
Jeżeli znamy objętość ostrosłupa (V) oraz pole jego podstawy (Pp), to możemy obliczyć wysokość ze wzoru na objętość ostrosłupa:
V = (1/3) * Pp * H
Przekształcając wzór, otrzymujemy:
H = (3 * V) / Pp
Przykład: Mamy ostrosłup o objętości 60 cm3 i polu podstawy 20 cm2. Zatem wysokość ostrosłupa:
H = (3 * 60) / 20 = 180 / 20 = 9 cm
Kiedy używać którego wzoru?
Wybór odpowiedniego wzoru zależy od danych, które posiadamy. Jeżeli znamy krawędź boczną i odległość spodka wysokości od wierzchołka podstawy, stosujemy twierdzenie Pitagorasa. Jeżeli znamy krawędź boczną i kąt nachylenia, stosujemy trygonometrię. Jeżeli znamy objętość i pole podstawy, korzystamy ze wzoru na objętość ostrosłupa. Często zadania wymagają połączenia kilku metod, np. obliczenia pola podstawy, a następnie wykorzystania go do obliczenia wysokości.
Praktyczne zastosowania
Obliczanie wysokości ostrosłupa ma wiele praktycznych zastosowań. Jest niezbędne w architekturze (np. przy projektowaniu piramid, dachów), inżynierii (np. przy obliczaniu wytrzymałości konstrukcji), a także w życiu codziennym (np. przy obliczaniu objętości pryzmatycznych pudełek o podstawie w kształcie wielokąta).
Podsumowując, zrozumienie pojęcia wysokości ostrosłupa oraz umiejętność jej obliczania jest bardzo ważne w geometrii przestrzennej. Pamiętajcie o trzech podstawowych metodach: twierdzeniu Pitagorasa, trygonometrii oraz wzorze na objętość. Ćwiczcie rozwiązywanie zadań, a na pewno opanujecie tę umiejętność!