Wzór Na Trojkat Rownoramienny Pole

Czy kiedykolwiek zastanawiałeś się, jak prosto i szybko obliczyć pole trójkąta równoramiennego? Być może potrzebujesz tego do projektu szkolnego, majsterkowania, czy nawet do zaplanowania ogrodu. Bez względu na powód, zrozumienie wzoru na pole trójkąta równoramiennego i jego praktyczne zastosowanie jest niezwykle przydatne.

Ten artykuł pomoże Ci zrozumieć, jak krok po kroku obliczyć pole trójkąta równoramiennego, wykorzystując różne dane, które możesz mieć dostępne. Postaramy się unikać skomplikowanego żargonu matematycznego i skupić się na praktycznych przykładach, które pomogą Ci zrozumieć koncepcję i zastosować ją w realnych sytuacjach.

Podstawy Trójkąta Równoramiennego

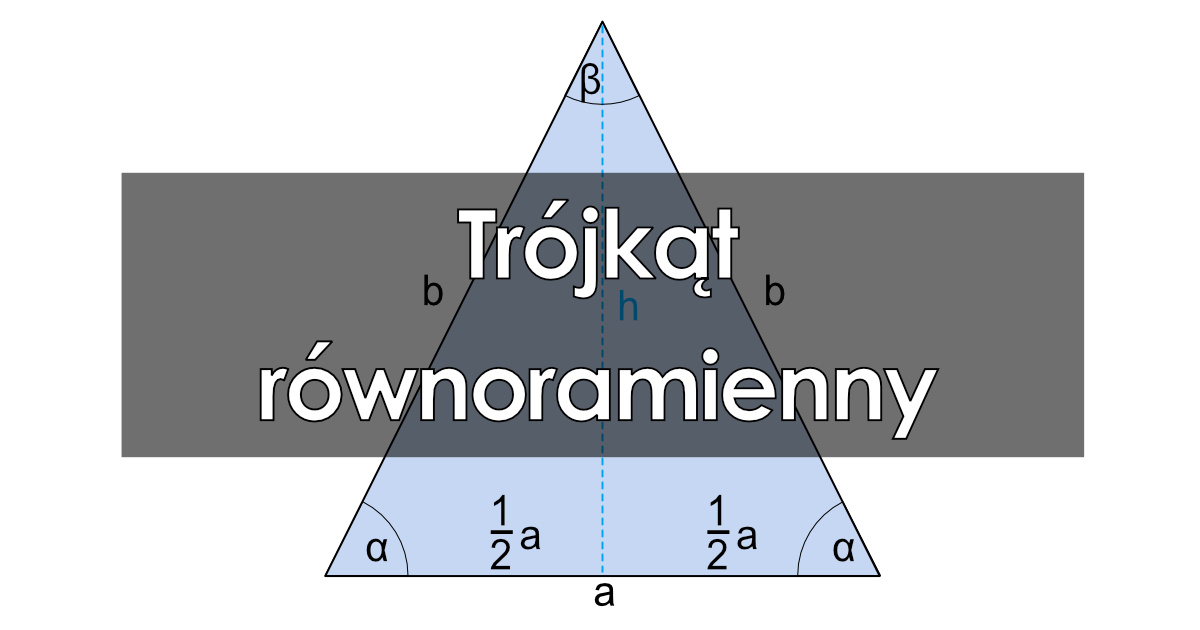
Zacznijmy od podstaw. Trójkąt równoramienny to taki trójkąt, który ma dwa boki równej długości. Te równe boki nazywamy ramionami, a trzeci bok to podstawa. Co więcej, kąty przy podstawie w trójkącie równoramiennym są zawsze równe.

Rozpoznawanie trójkąta równoramiennego jest kluczowe, ponieważ pozwala nam wykorzystać jego specyficzne właściwości do uproszczenia obliczeń. Na przykład, wysokość poprowadzona z wierzchołka pomiędzy ramionami (wierzchołek kąta między ramionami) dzieli podstawę na dwie równe części i jest prostopadła do podstawy. To bardzo ważna informacja!

Wzór Podstawowy na Pole Trójkąta Równoramiennego

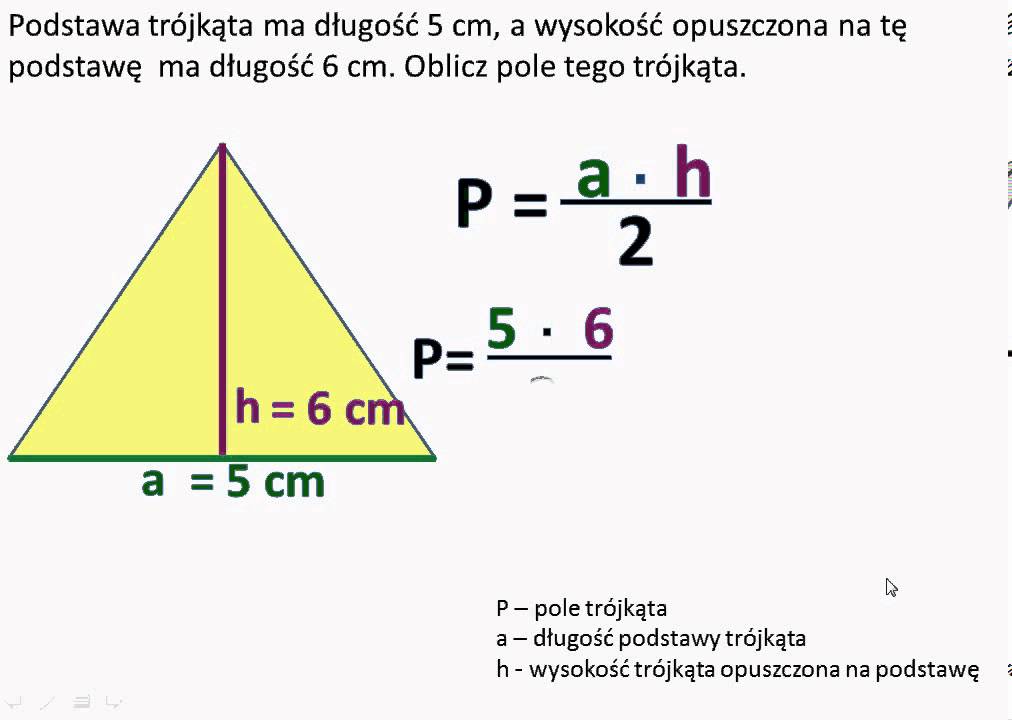
Najbardziej podstawowy wzór na pole każdego trójkąta to:

Pole = (1/2) * podstawa * wysokość

Gdzie:

podstawa to długość podstawy trójkąta.
wysokość to odległość od podstawy do wierzchołka leżącego naprzeciwko podstawy, mierzona pod kątem prostym.

W przypadku trójkąta równoramiennego, jeśli znamy długość podstawy (a) i wysokość (h) opuszczoną na tę podstawę, możemy bezpośrednio zastosować ten wzór. To najprostszy i najczęściej wykorzystywany sposób.

Przykład 1: Znamy podstawę i wysokość

Załóżmy, że mamy trójkąt równoramienny o podstawie a = 10 cm i wysokości h = 7 cm. Jak obliczyć jego pole?

Zastosujmy wzór:

Pole = (1/2) * 10 cm * 7 cm = 35 cm²

Proste, prawda?

Wzór na Pole, Znając Długość Ramion i Podstawy

Co zrobić, jeśli nie znamy wysokości, ale znamy długość ramion (b) i podstawy (a)? Możemy wtedy wykorzystać twierdzenie Pitagorasa, aby obliczyć wysokość, a następnie użyć podstawowego wzoru na pole.

W trójkącie równoramiennym wysokość opuszczona na podstawę dzieli ją na dwie równe części. Oznacza to, że tworzy ona dwa trójkąty prostokątne. W każdym z tych trójkątów:

b (długość ramienia) jest przeciwprostokątną.
a/2 (połowa długości podstawy) jest jedną z przyprostokątnych.
h (wysokość) jest drugą przyprostokątną.

Zgodnie z twierdzeniem Pitagorasa:

b² = (a/2)² + h²

Możemy przekształcić ten wzór, aby wyznaczyć h:

h = √(b² - (a/2)²)

Po obliczeniu wysokości, możemy wrócić do podstawowego wzoru na pole: Pole = (1/2) * a * h.

Przykład 2: Znamy ramiona i podstawę

Załóżmy, że mamy trójkąt równoramienny o ramionach długości b = 8 cm i podstawie a = 6 cm. Obliczmy pole.

Obliczamy wysokość: h = √(8² - (6/2)²) = √(64 - 9) = √55 ≈ 7.42 cm
Obliczamy pole: Pole = (1/2) * 6 cm * 7.42 cm ≈ 22.26 cm²

Wzór Herona dla Trójkąta Równoramiennego

Wzór Herona to uniwersalny wzór na obliczanie pola trójkąta, znając długości wszystkich jego boków. Można go użyć również dla trójkąta równoramiennego. Najpierw obliczamy połowę obwodu trójkąta, zwaną p (czasami oznaczaną jako s):

p = (a + b + b) / 2 = (a + 2b) / 2

Gdzie:

a to długość podstawy.
b to długość ramienia.

Następnie obliczamy pole, korzystając ze wzoru Herona:

Pole = √(p * (p - a) * (p - b) * (p - b))

Przykład 3: Wykorzystanie Wzoru Herona

Użyjmy tych samych wartości co w przykładzie 2: a = 6 cm i b = 8 cm.

Obliczamy połowę obwodu: p = (6 + 8 + 8) / 2 = 11 cm
Obliczamy pole: Pole = √(11 * (11 - 6) * (11 - 8) * (11 - 8)) = √(11 * 5 * 3 * 3) = √495 ≈ 22.25 cm²

Jak widzisz, wynik jest bardzo zbliżony do tego, który uzyskaliśmy, używając twierdzenia Pitagorasa. Różnice wynikają z zaokrągleń podczas obliczeń.

Kiedy Używać Którego Wzoru?

Wybór odpowiedniego wzoru zależy od danych, które masz dostępne:

Jeśli znasz podstawę i wysokość: Użyj wzoru Pole = (1/2) * podstawa * wysokość. To najprostsza i najszybsza metoda.
Jeśli znasz podstawę i długość ramion: Użyj twierdzenia Pitagorasa, aby obliczyć wysokość, a następnie podstawowy wzór na pole. Alternatywnie, możesz użyć wzoru Herona.
Jeśli znasz tylko długości boków: Wzór Herona jest jedynym rozwiązaniem.

Praktyczne Zastosowania

Obliczanie pola trójkąta równoramiennego ma wiele praktycznych zastosowań:

Architektura i budownictwo: Do obliczania powierzchni dachów, elewacji, elementów dekoracyjnych.
Projektowanie wnętrz: Do obliczania ilości materiałów potrzebnych do wykończenia ścian o nietypowym kształcie.
Majsterkowanie: Do wycinania elementów z drewna lub innych materiałów.
Geodezja i kartografia: Do obliczania powierzchni działek i terenów.
Gry komputerowe i grafika: Do modelowania obiektów 3D.

Na przykład, jeśli projektujesz dach w kształcie trójkąta równoramiennego i wiesz, że podstawa dachu ma 12 metrów, a długość krokwi (ramienia trójkąta) to 7 metrów, możesz obliczyć pole dachu, aby oszacować ilość potrzebnych dachówek. Albo, jeśli chcesz uszyć żagiel w kształcie trójkąta równoramiennego, obliczenie pola pomoże Ci określić, ile materiału musisz kupić.

Podsumowanie

Obliczanie pola trójkąta równoramiennego jest łatwe i przyjemne, jeśli zna się odpowiednie wzory i wie, jak je zastosować. Pamiętaj o kilku kluczowych rzeczach:

Trójkąt równoramienny ma dwa równe boki (ramiona) i dwa równe kąty przy podstawie.
Podstawowy wzór na pole to Pole = (1/2) * podstawa * wysokość.
Jeśli nie znasz wysokości, możesz ją obliczyć, korzystając z twierdzenia Pitagorasa lub wzoru Herona.
Wybierz wzór odpowiedni do danych, które masz dostępne.

Mam nadzieję, że ten artykuł rozwiał Twoje wątpliwości i teraz obliczanie pola trójkąta równoramiennego nie będzie już dla Ciebie żadnym problemem. Powodzenia!