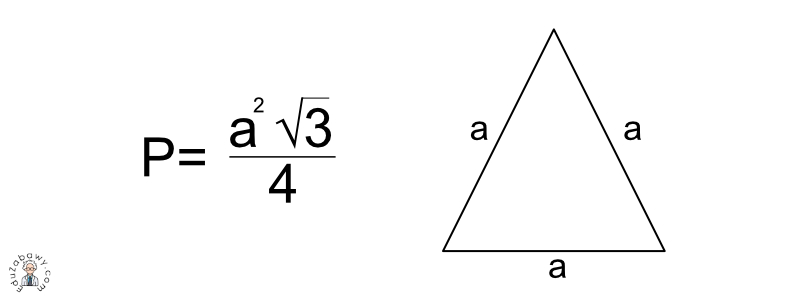Wzór Na Trojkat Rownoboczny Pole

W geometrii euklidesowej trójkąt równoboczny to figura o trzech równych bokach i trzech równych kątach, każdy o mierze 60 stopni. Jego elegancka symetria i prostota sprawiają, że jest to jeden z najczęściej badanych i wykorzystywanych kształtów. Obliczanie jego pola powierzchni jest podstawową umiejętnością matematyczną, a zrozumienie wzoru na pole trójkąta równobocznego otwiera drzwi do rozwiązywania wielu problemów praktycznych. Niniejszy artykuł ma na celu dogłębne omówienie tego wzoru, jego wyprowadzenia oraz zastosowań.
Podstawowe Własności Trójkąta Równobocznego
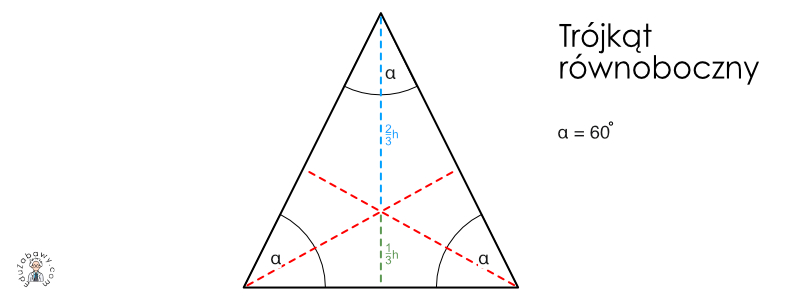
Zanim przejdziemy do samego wzoru na pole, warto przypomnieć sobie najważniejsze cechy trójkąta równobocznego. Wszystkie trzy boki mają identyczną długość, a każdy z trzech kątów wewnętrznych wynosi dokładnie 60 stopni. Ponadto, trójkąt równoboczny jest figurą foremną, co oznacza, że posiada najwyższą możliwą symetrię. Wysokość w trójkącie równobocznym (linia prostopadła opuszczona z wierzchołka na przeciwległy bok) jest również środkową (dzieli bok na dwie równe części) oraz dwusieczną kąta (dzieli kąt na dwie równe części). Te unikalne właściwości upraszczają wiele obliczeń, w tym obliczanie pola powierzchni.
Dlaczego Warto Znać Wzór na Pole?
Znajomość wzoru na pole trójkąta równobocznego jest kluczowa nie tylko w matematyce, ale również w wielu dziedzinach nauki i inżynierii. Architekci wykorzystują go przy projektowaniu konstrukcji, inżynierowie przy obliczaniu wytrzymałości materiałów, a nawet w grafice komputerowej przy tworzeniu realistycznych obrazów. Zrozumienie tego wzoru pozwala na szybkie i efektywne rozwiązywanie problemów związanych z geometrią i przestrzenią.
Wzór na Pole Trójkąta Równobocznego: Wprowadzenie
Najpopularniejszy i najczęściej używany wzór na pole trójkąta równobocznego, gdzie znana jest długość boku a, to:
P = (a² * √3) / 4
Gdzie:
- P oznacza pole powierzchni trójkąta.
- a oznacza długość boku trójkąta równobocznego.
- √3 oznacza pierwiastek kwadratowy z 3 (w przybliżeniu 1.732).
Wzór ten pozwala na bezpośrednie obliczenie pola, znając jedynie długość boku trójkąta.
Wyprowadzenie Wzoru na Pole Trójkąta Równobocznego
Wzór ten nie pojawia się znikąd. Istnieje kilka sposobów na jego wyprowadzenie, a zrozumienie tego procesu pomaga lepiej zapamiętać i zastosować wzór.
Wyprowadzenie z Ogólnego Wzoru na Pole Trójkąta
Zacznijmy od ogólnego wzoru na pole trójkąta: P = (1/2) * podstawa * wysokość. W przypadku trójkąta równobocznego, podstawa to po prostu bok a. Problem polega na znalezieniu wysokości h. Wykorzystujemy tutaj fakt, że wysokość dzieli trójkąt równoboczny na dwa identyczne trójkąty prostokątne.
W każdym z tych trójkątów prostokątnych, przeciwprostokątna to bok a, jedna z przyprostokątnych to połowa boku (a/2), a druga przyprostokątna to wysokość h. Możemy zatem zastosować twierdzenie Pitagorasa: a² = (a/2)² + h².
Przekształcając to równanie, otrzymujemy: h² = a² - (a²/4) = (3a²/4). Zatem wysokość h = √(3a²/4) = (a√3)/2.
Teraz możemy podstawić wartość wysokości do ogólnego wzoru na pole: P = (1/2) * a * (a√3)/2 = (a²√3)/4. W ten sposób wyprowadziliśmy wzór na pole trójkąta równobocznego.
Wyprowadzenie z Trygonometrii
Pole trójkąta można również obliczyć za pomocą wzoru trygonometrycznego: P = (1/2) * a * b * sin(γ), gdzie a i b to długości dwóch boków trójkąta, a γ to kąt pomiędzy nimi. W przypadku trójkąta równobocznego, a = b, a γ = 60°. Wiemy, że sin(60°) = √3/2.
Podstawiając te wartości do wzoru, otrzymujemy: P = (1/2) * a * a * (√3/2) = (a²√3)/4. Otrzymujemy ten sam wzór, co potwierdza jego poprawność.
Zastosowania Wzoru w Praktyce
Wzór na pole trójkąta równobocznego ma szerokie zastosowanie w różnych dziedzinach.
Architektura i Budownictwo
Architekci często wykorzystują trójkąty równoboczne w swoich projektach ze względu na ich stabilność i estetykę. Na przykład, mogą być one użyte jako elementy konstrukcyjne dachów, mostów, a także w dekoracyjnych detalach. Obliczenie pola trójkąta równobocznego jest niezbędne do określenia ilości materiału potrzebnego do budowy danego elementu.
Inżynieria
Inżynierowie wykorzystują wzór na pole trójkąta równobocznego do obliczania wytrzymałości różnych konstrukcji. Na przykład, w analizie naprężeń i odkształceń, znajomość pola powierzchni elementu trójkątnego jest kluczowa do określenia, jak będzie on reagował na obciążenia. Trójkątne elementy są często używane do wzmacniania konstrukcji, a ich odpowiednie zaprojektowanie wymaga precyzyjnych obliczeń.
Grafika Komputerowa
W grafice komputerowej, trójkąty są podstawowym elementem do tworzenia modeli 3D. Siatki trójkątów pozwalają na reprezentację skomplikowanych kształtów i powierzchni. Wzór na pole trójkąta równobocznego może być użyty do obliczania powierzchni tekstur, oświetlenia oraz do optymalizacji renderingu.
Projektowanie Gier
Podobnie jak w grafice komputerowej, w projektowaniu gier trójkąty są szeroko stosowane do tworzenia środowisk i postaci. Obliczanie pola powierzchni trójkątów jest ważne dla fizyki gry, kolizji obiektów oraz optymalizacji wydajności.
Przykład Numeryczny
Załóżmy, że mamy trójkąt równoboczny o boku a = 10 cm. Chcemy obliczyć jego pole powierzchni. Stosując wzór, otrzymujemy:
P = (10² * √3) / 4 = (100 * √3) / 4 = 25√3 cm²
W przybliżeniu, pole powierzchni tego trójkąta wynosi 25 * 1.732 = 43.3 cm².
Alternatywne Wzory i Metody Obliczania
Oprócz podstawowego wzoru, istnieją inne metody obliczania pola trójkąta równobocznego, które mogą być przydatne w zależności od dostępnych danych.
Z Pomocą Wysokości (h)
Jeżeli znamy wysokość h trójkąta równobocznego, możemy obliczyć jego pole, wykorzystując fakt, że a = (2h) / √3. Podstawiając to do podstawowego wzoru, otrzymujemy:
P = (((2h) / √3)² * √3) / 4 = (4h² / 3 * √3) / 4 = (h²√3) / 3
Zatem, P = (h²√3) / 3. Ten wzór jest użyteczny, gdy znamy wysokość, a nie długość boku.
Kalkulatory Online
W dzisiejszych czasach istnieje wiele kalkulatorów online, które pozwalają na szybkie obliczenie pola trójkąta równobocznego. Wystarczy wpisać długość boku, a kalkulator automatycznie obliczy pole. Takie narzędzia są szczególnie przydatne, gdy potrzebujemy szybko uzyskać wynik bez konieczności wykonywania ręcznych obliczeń.
Podsumowanie
Wzór na pole trójkąta równobocznego: P = (a² * √3) / 4 jest fundamentalnym narzędziem w geometrii i ma szerokie zastosowanie w różnych dziedzinach nauki i inżynierii. Zrozumienie jego wyprowadzenia oraz praktyczne zastosowanie pozwala na efektywne rozwiązywanie problemów związanych z geometrią i przestrzenią. Pamiętaj, że znajomość tego wzoru to inwestycja w Twoją wiedzę i umiejętności.
Zachęcamy do dalszego eksplorowania geometrii i matematyki. Ćwicz obliczenia, eksperymentuj z różnymi wartościami i odkrywaj nowe zastosowania tego fascynującego wzoru!