Wzor Na Ruch Jednostajnie Przyspieszony

Czy kiedykolwiek zastanawiałeś się, jak fizycy obliczają, jak szybko samochód przyspiesza lub jak daleko doleci piłka wyrzucona w górę? Odpowiedź tkwi w zrozumieniu ruchu jednostajnie przyspieszonego i wzoru, który go opisuje. Wielu uczniów i studentów ma trudności z opanowaniem tego zagadnienia, czując się zagubionymi w gąszczu wzorów i definicji. Spróbujmy to zmienić.

Celem tego artykułu jest wyjaśnienie wzoru na ruch jednostajnie przyspieszony w sposób prosty, zrozumiały i praktyczny, tak abyś mógł z łatwością stosować go w rozwiązywaniu problemów i analizie rzeczywistych sytuacji.

Czym jest ruch jednostajnie przyspieszony?

Zanim przejdziemy do wzoru, musimy zrozumieć, co to tak naprawdę jest ruch jednostajnie przyspieszony. Jest to ruch, w którym prędkość ciała zmienia się w czasie w sposób jednostajny, czyli o stałą wartość w jednostce czasu. Innymi słowy, przyspieszenie jest stałe.

Pomyśl o samochodzie, który rusza z miejsca i stopniowo zwiększa swoją prędkość. Jeśli prędkość rośnie o taką samą wartość co sekundę (np. o 2 m/s co sekundę), to mamy do czynienia z ruchem jednostajnie przyspieszonym.

W przeciwieństwie do ruchu jednostajnego, gdzie prędkość jest stała, w ruchu jednostajnie przyspieszonym przyspieszenie jest kluczowym parametrem. Przyspieszenie (oznaczane symbolem a) mierzy, jak szybko zmienia się prędkość ciała.

Wzór na ruch jednostajnie przyspieszony: podstawa fizyki

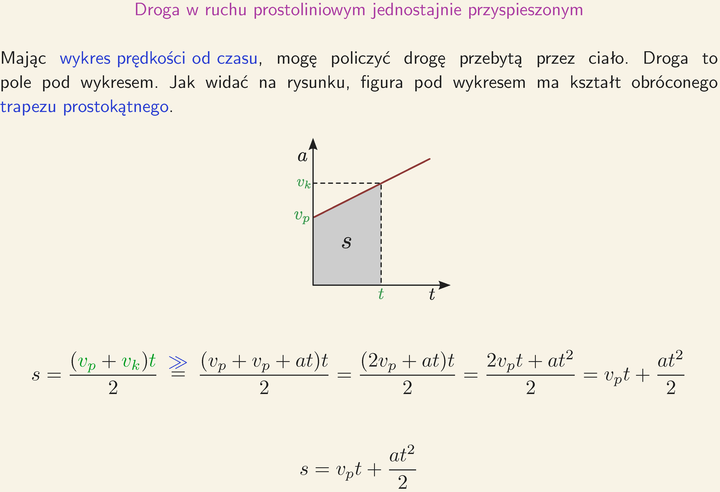
Podstawowym wzorem opisującym ruch jednostajnie przyspieszony jest wzór na drogę:

s = v₀t + (1/2)at²

Gdzie:

s oznacza przebytą drogę.
v₀ (czyt. ve zero) oznacza prędkość początkową.
t oznacza czas trwania ruchu.
a oznacza przyspieszenie.

Wzór ten pozwala nam obliczyć, jak daleko przesunie się ciało w danym czasie, znając jego prędkość początkową i przyspieszenie. Zauważmy, że droga zależy od czasu w kwadracie (t²), co oznacza, że im dłużej trwa ruch, tym szybciej rośnie pokonana odległość.

Wyjaśnienie elementów wzoru

Przyjrzyjmy się bliżej każdemu elementowi wzoru:

Droga (s): Mierzona w metrach (m) lub kilometrach (km), informuje nas, jak daleko przesunęło się ciało od punktu początkowego.
Prędkość początkowa (v₀): Mierzona w metrach na sekundę (m/s) lub kilometrach na godzinę (km/h), to prędkość, z jaką ciało poruszało się w momencie rozpoczęcia obserwacji. Jeśli ciało startuje z miejsca, v₀ wynosi 0.
Czas (t): Mierzony w sekundach (s) lub godzinach (h), to okres, w którym trwa ruch.
Przyspieszenie (a): Mierzone w metrach na sekundę kwadrat (m/s²), informuje nas, o ile zmienia się prędkość ciała w ciągu jednej sekundy.

Inne przydatne wzory

Oprócz wzoru na drogę, istnieją inne wzory, które mogą być przydatne w analizie ruchu jednostajnie przyspieszonego:

Wzór na prędkość końcową (v): v = v₀ + at
Wzór na drogę bez znajomości czasu: v² = v₀² + 2as (ten wzór jest szczególnie przydatny, gdy nie mamy podanego czasu trwania ruchu)

Te wzory pozwalają nam obliczyć prędkość końcową ciała po upływie danego czasu lub obliczyć drogę, jaką ciało pokonało, znając jego prędkości początkową i końcową oraz przyspieszenie.

Przykłady zastosowania wzoru w praktyce

Aby lepiej zrozumieć, jak działa wzór na ruch jednostajnie przyspieszony, przeanalizujmy kilka przykładów:

Przykład 1: Samochód rusza z miejsca (v₀ = 0 m/s) i przyspiesza z przyspieszeniem a = 2 m/s² przez 5 sekund. Jaką drogę pokona w tym czasie?

Rozwiązanie: Używamy wzoru s = v₀t + (1/2)at². Podstawiamy wartości: s = (0 m/s)(5 s) + (1/2)(2 m/s²)(5 s)² = 0 + (1 m/s²)(25 s²) = 25 m. Samochód pokona 25 metrów.

Przykład 2: Rowerzysta jedzie z prędkością początkową v₀ = 5 m/s i zaczyna hamować z przyspieszeniem a = -1 m/s² (ujemne, ponieważ hamuje). Jaką drogę przebędzie, zanim się zatrzyma?

Rozwiązanie: Tutaj musimy najpierw obliczyć czas, po którym rowerzysta się zatrzyma. Używamy wzoru v = v₀ + at. W momencie zatrzymania v = 0 m/s. Zatem 0 = 5 m/s + (-1 m/s²)t. Przekształcamy równanie: t = 5 s. Teraz możemy obliczyć drogę: s = v₀t + (1/2)at² = (5 m/s)(5 s) + (1/2)(-1 m/s²)(5 s)² = 25 m - 12.5 m = 12.5 m. Rowerzysta przebędzie 12.5 metra, zanim się zatrzyma.

Przykład 3: Spadający swobodnie przedmiot (pomijamy opór powietrza) przyspiesza z przyspieszeniem ziemskim g = 9.81 m/s². Jaką prędkość osiągnie po 3 sekundach spadania, startując z zerowej prędkości początkowej?

Rozwiązanie: Używamy wzoru v = v₀ + at = 0 + (9.81 m/s²)*3 s = 29.43 m/s. Prędkość po 3 sekundach to 29.43 m/s.

Kiedy ruch nie jest jednostajnie przyspieszony?

Ważne jest, aby pamiętać, że wzory na ruch jednostajnie przyspieszony mają zastosowanie tylko wtedy, gdy przyspieszenie jest stałe. Istnieją sytuacje, w których przyspieszenie się zmienia, a wtedy musimy stosować bardziej zaawansowane metody analizy.

Przykłady sytuacji, gdzie ruch nie jest jednostajnie przyspieszony:

Samochód gwałtownie przyspieszający, a następnie hamujący.
Ruch wahadła.
Ruch z uwzględnieniem oporu powietrza, który zależy od prędkości.

W takich przypadkach przyspieszenie nie jest stałe i musimy stosować inne metody, np. rachunek różniczkowy i całkowy, aby dokładnie opisać ruch.

Praktyczne wskazówki dotyczące rozwiązywania zadań

Oto kilka praktycznych wskazówek, które pomogą Ci w rozwiązywaniu zadań z ruchu jednostajnie przyspieszonego:

Przeczytaj uważnie treść zadania: Zwróć uwagę na dane, które są podane, i na to, co masz obliczyć.
Zapisz wszystkie dane i niewiadome: Uporządkuj informacje, aby uniknąć pomyłek.
Wybierz odpowiedni wzór: Zastanów się, który wzór najlepiej pasuje do danej sytuacji. Często trzeba użyć kilku wzorów, aby rozwiązać zadanie.
Upewnij się, że jednostki są zgodne: Przekształć jednostki, jeśli to konieczne, aby wszystkie były w tym samym systemie (np. metry, sekundy).
Sprawdź wynik: Zastanów się, czy wynik jest sensowny w kontekście zadania. Czy samochód naprawdę mógłby osiągnąć taką prędkość w tak krótkim czasie?
Rysuj schematy: Wizualizacja problemu często pomaga w jego zrozumieniu i rozwiązaniu.

Podsumowanie

Wzór na ruch jednostajnie przyspieszony jest podstawowym narzędziem do analizy ruchu, w którym prędkość zmienia się w czasie w sposób jednostajny. Zrozumienie tego wzoru i umiejętność jego stosowania pozwala na rozwiązywanie wielu problemów z fizyki i analizowanie rzeczywistych sytuacji. Pamiętaj, że kluczem do sukcesu jest praktyka i rozwiązywanie jak największej liczby zadań.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć wzór na ruch jednostajnie przyspieszony. Powodzenia w dalszej nauce fizyki!