Wzór Na Przyspieszenie W Ruchu Jednostajnie Przyspieszonym

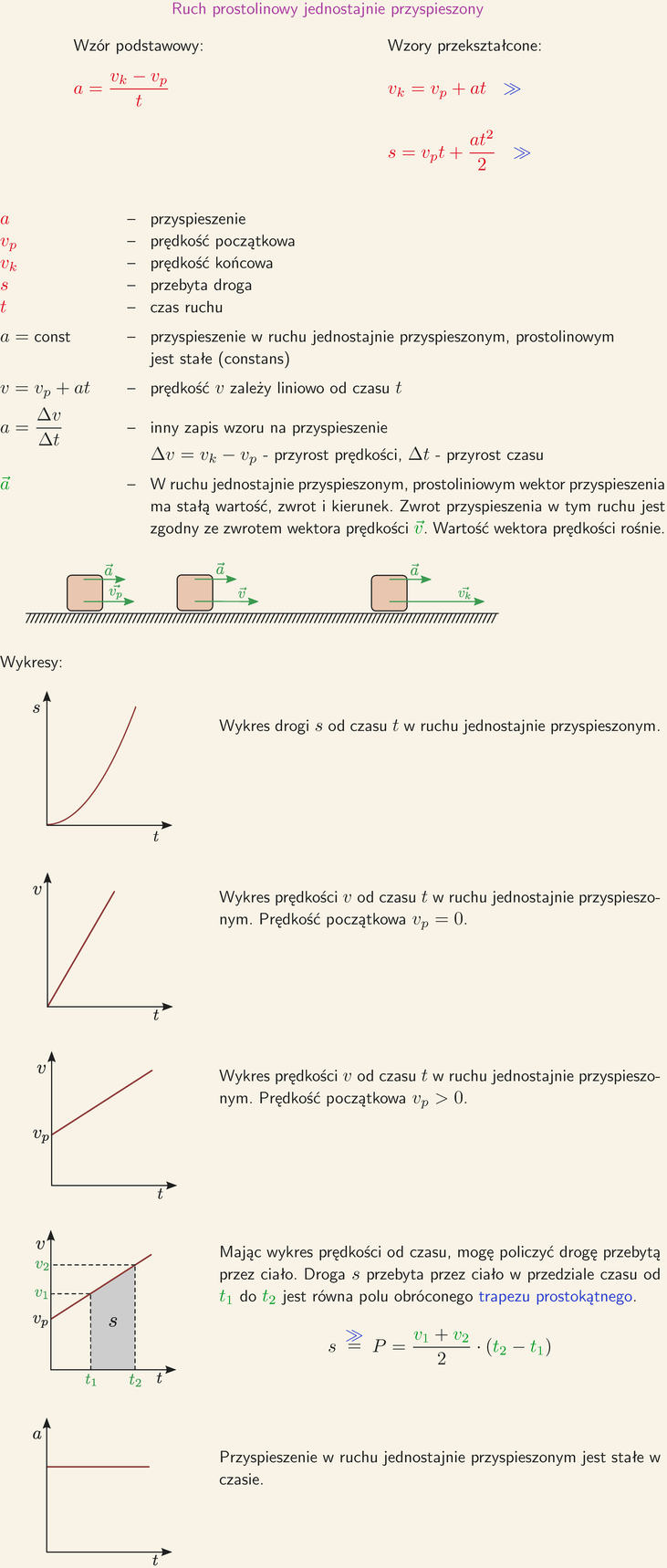
Ruch jednostajnie przyspieszony, jak sama nazwa wskazuje, charakteryzuje się stałym przyspieszeniem. To oznacza, że prędkość ciała zmienia się w sposób liniowy w czasie. Zrozumienie tego ruchu jest kluczowe w fizyce, ponieważ wiele zjawisk w naszym otoczeniu można opisać za pomocą tego modelu. Aby zgłębić istotę ruchu jednostajnie przyspieszonego, niezbędne jest poznanie wzoru na przyspieszenie.

Przyspieszenie definiujemy jako zmianę prędkości w czasie. Formalnie, przyspieszenie (a) to iloraz zmiany prędkości (Δv) przez czas (Δt), w którym ta zmiana nastąpiła. Matematycznie zapisujemy to jako:

a = Δv / Δt

Δv to różnica między prędkością końcową (vk) a prędkością początkową (v0):

Δv = vk - v0

Podstawiając to do wzoru na przyspieszenie, otrzymujemy:

a = (vk - v0) / Δt

Z powyższego wzoru możemy wywnioskować kilka istotnych faktów. Po pierwsze, przyspieszenie jest wektorem, co oznacza, że ma zarówno wartość, jak i kierunek. Po drugie, jednostką przyspieszenia w układzie SI jest metr na sekundę kwadratową (m/s²). Informuje nas to, o ile metrów na sekundę zmienia się prędkość ciała co sekundę.

Przekształcając wzór na przyspieszenie, możemy wyprowadzić wzór na prędkość końcową w ruchu jednostajnie przyspieszonym:

vk = v0 + a * Δt

Ten wzór pozwala nam obliczyć prędkość ciała po upływie określonego czasu, znając prędkość początkową i przyspieszenie.

Droga w ruchu jednostajnie przyspieszonym

Aby obliczyć drogę przebytą przez ciało w ruchu jednostajnie przyspieszonym, potrzebujemy kolejnego wzoru. Wzór na drogę (s) w ruchu jednostajnie przyspieszonym z prędkością początkową v0, przyspieszeniem a i czasem t wygląda następująco:

s = v0 * t + (1/2) * a * t²

Ten wzór uwzględnia zarówno prędkość początkową, jak i przyspieszenie. Jeśli ciało rozpoczyna ruch z prędkością początkową równą zero (v0 = 0), wzór upraszcza się do:

s = (1/2) * a * t²

Warto zwrócić uwagę, że droga rośnie kwadratowo wraz z czasem, co jest charakterystyczne dla ruchu jednostajnie przyspieszonego.

Rozważmy teraz kilka przykładów, aby lepiej zrozumieć, jak stosować te wzory w praktyce.

Przykład 1:

Samochód rusza z miejsca (v0 = 0 m/s) i przyspiesza jednostajnie z przyspieszeniem a = 2 m/s² przez 5 sekund. Oblicz prędkość końcową samochodu.

Rozwiązanie:

Korzystamy ze wzoru na prędkość końcową:

vk = v0 + a * t vk = 0 + 2 m/s² * 5 s vk = 10 m/s

Odpowiedź: Prędkość końcowa samochodu wynosi 10 m/s.

Przykład 2:

Pociąg jadący z prędkością 20 m/s zaczyna hamować z przyspieszeniem -1 m/s². Oblicz czas, po którym pociąg się zatrzyma.

Rozwiązanie:

Prędkość końcowa pociągu wynosi 0 m/s. Korzystamy ze wzoru na przyspieszenie, przekształcając go, aby wyznaczyć czas:

a = (vk - v0) / t t = (vk - v0) / a t = (0 m/s - 20 m/s) / -1 m/s² t = 20 s

Odpowiedź: Pociąg zatrzyma się po 20 sekundach.

Przykład 3:

Rowerzysta rusza z miejsca i przyspiesza z przyspieszeniem 0.5 m/s² przez 10 sekund. Oblicz, jaką drogę pokona rowerzysta w tym czasie.

Rozwiązanie:

Korzystamy ze wzoru na drogę w ruchu jednostajnie przyspieszonym z prędkością początkową równą zero:

s = (1/2) * a * t² s = (1/2) * 0.5 m/s² * (10 s)² s = (1/2) * 0.5 m/s² * 100 s² s = 25 m

Odpowiedź: Rowerzysta pokona drogę 25 metrów.

Warto zauważyć, że przyspieszenie może być zarówno dodatnie, jak i ujemne. Dodatnie przyspieszenie oznacza, że prędkość ciała rośnie, natomiast ujemne przyspieszenie (często nazywane opóźnieniem) oznacza, że prędkość ciała maleje.

Znaczenie przyspieszenia w życiu codziennym jest ogromne. Bez przyspieszenia nie moglibyśmy ruszyć samochodem, pociągiem ani samolotem. Przyspieszenie odgrywa również kluczową rolę w sporcie, na przykład podczas sprintu, rzutu oszczepem czy skoku w dal. Nawet chodzenie jest przykładem ruchu z przyspieszeniem, choć na bardzo krótkich odcinkach czasu.

Zrozumienie wzoru na przyspieszenie w ruchu jednostajnie przyspieszonym otwiera drzwi do zrozumienia wielu zjawisk fizycznych, które obserwujemy na co dzień. Pozwala nam przewidywać ruch ciał, obliczać prędkości i drogi, a także projektować urządzenia i systemy, które wykorzystują ruch przyspieszony.

Pamiętajmy, że model ruchu jednostajnie przyspieszonego jest pewnym uproszczeniem rzeczywistości. W praktyce, przyspieszenie rzadko jest idealnie stałe. Często mamy do czynienia z ruchem zmiennym, w którym przyspieszenie zmienia się w czasie. Niemniej jednak, zrozumienie ruchu jednostajnie przyspieszonego stanowi solidną podstawę do analizy bardziej złożonych ruchów.