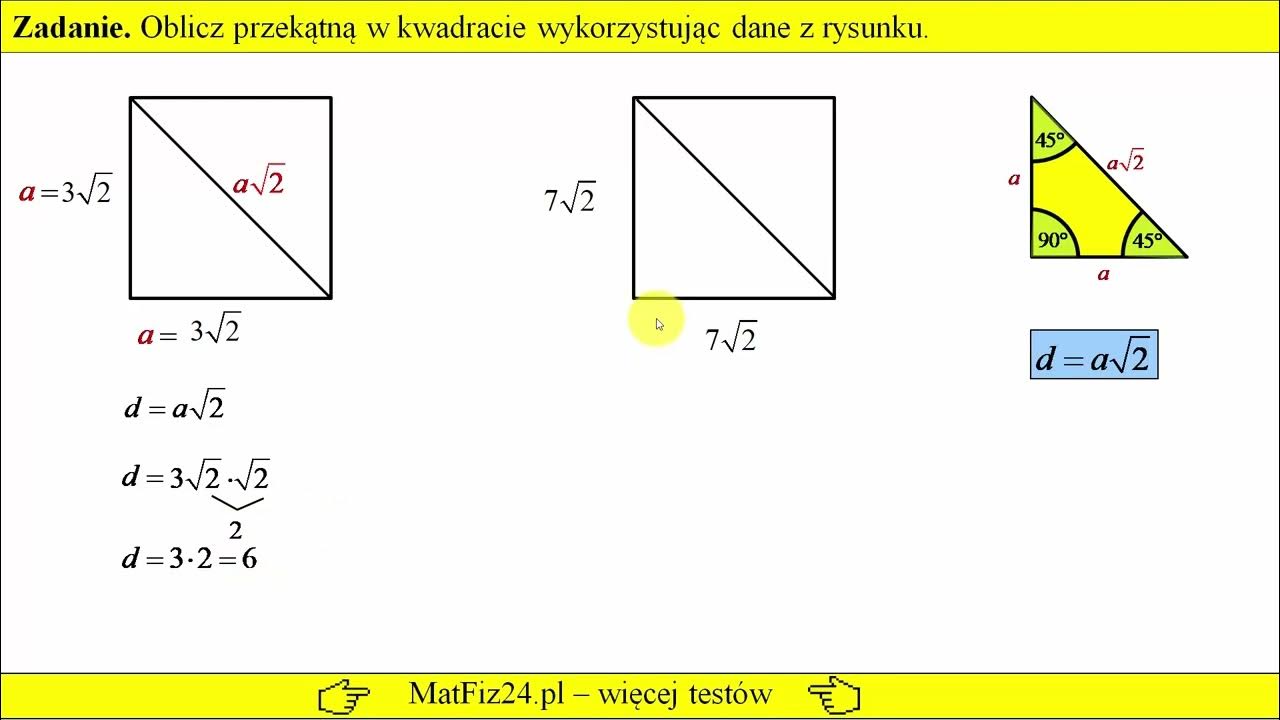
Wzór Na Przekątną W Kwadracie

Czy kiedykolwiek zastanawiałeś się, jak szybko obliczyć długość przekątnej kwadratu, mając daną tylko długość jego boku? Dla wielu osób geometria wydaje się być odległą krainą wzorów i reguł, jednak w praktyce, zrozumienie podstawowych koncepcji, takich jak wzór na przekątną kwadratu, może okazać się niezwykle przydatne w życiu codziennym i zawodowym. Niezależnie od tego, czy jesteś uczniem, studentem, inżynierem, czy po prostu osobą lubiącą rozwiązywać łamigłówki, ten artykuł pomoże Ci opanować tę wiedzę.

W tym artykule rozłożymy na czynniki pierwsze wzór na przekątną kwadratu. Zobaczymy skąd się bierze, jak go używać i w jakich sytuacjach może być dla nas szczególnie pomocny. Zapomnij o suchych definicjach i skomplikowanych obliczeniach. Postaramy się przedstawić to zagadnienie w sposób jasny, zrozumiały i przede wszystkim – praktyczny.

Rozumienie Podstaw: Czym Jest Kwadrat i Jego Przekątna?

Zanim przejdziemy do konkretnego wzoru, upewnijmy się, że dobrze rozumiemy podstawowe pojęcia. Kwadrat to czworokąt foremny, czyli figura geometryczna, która ma wszystkie boki równe i wszystkie kąty proste (90 stopni). To bardzo ważne! Ta symetria i prostota kwadratu sprawia, że obliczenia z nim związane są stosunkowo proste.

Przekątna kwadratu to odcinek łączący dwa przeciwległe wierzchołki. Innymi słowy, to linia, która przecina kwadrat od rogu do rogu. Kwadrat ma dwie przekątne, które przecinają się w punkcie środkowym kwadratu pod kątem prostym, dzieląc go na cztery identyczne trójkąty prostokątne równoramienne. To również istotne, ponieważ wykorzystamy tę wiedzę do wyprowadzenia wzoru.

Wyprowadzenie Wzoru na Przekątną Kwadratu: Twierdzenie Pitagorasa w Akcji

Teraz przejdźmy do sedna – wzoru na przekątną kwadratu. Wzór ten jest prosty i elegancki:

d = a√2

Gdzie:

• d oznacza długość przekątnej kwadratu.
• a oznacza długość boku kwadratu.

Ale skąd się bierze ten wzór? Odpowiedź kryje się w Twierdzeniu Pitagorasa. Pamiętasz je z lekcji matematyki? Twierdzenie to mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych (boków przylegających do kąta prostego) jest równa kwadratowi długości przeciwprostokątnej (boku naprzeciwko kąta prostego). Wzór ten brzmi następująco:

a² + b² = c²

W naszym przypadku przekątna kwadratu dzieli go na dwa trójkąty prostokątne równoramienne. Boki kwadratu (a) stają się przyprostokątnymi tych trójkątów, a przekątna (d) staje się przeciwprostokątną. Zatem możemy zastosować Twierdzenie Pitagorasa:

a² + a² = d²

Uprośćmy to:

2a² = d²

Teraz wyciągamy pierwiastek kwadratowy z obu stron równania:

√(2a²) = √d²

Co daje nam:

a√2 = d

Czyli dokładnie to, co chcieliśmy udowodnić! Wzór na przekątną kwadratu (d = a√2) wynika bezpośrednio z Twierdzenia Pitagorasa.

Przykłady Zastosowania Wzoru

Żeby lepiej zrozumieć, jak działa wzór na przekątną kwadratu, przeanalizujmy kilka przykładów:

Przykład 1: Załóżmy, że mamy kwadrat o boku długości 5 cm. Jak obliczyć długość jego przekątnej?

Używamy wzoru: d = a√2

Podstawiamy: d = 5√2

Wynik: d ≈ 5 * 1.414 ≈ 7.07 cm

Czyli przekątna tego kwadratu ma około 7.07 cm długości.

Przykład 2: Mamy kwadratowy plac, którego bok ma długość 12 metrów. Chcemy przeciągnąć kabel po przekątnej placu. Jak długi musi być kabel?

Używamy wzoru: d = a√2

Podstawiamy: d = 12√2

Wynik: d ≈ 12 * 1.414 ≈ 16.97 metrów

Potrzebujemy kabla o długości około 16.97 metrów.

Przykład 3: Wiemy, że przekątna kwadratu ma długość 10 cm. Jak obliczyć długość jego boku?

Tutaj musimy przekształcić wzór. Skoro d = a√2, to a = d / √2

Podstawiamy: a = 10 / √2

Żeby pozbyć się pierwiastka z mianownika, mnożymy licznik i mianownik przez √2:

a = (10√2) / 2

Wynik: a = 5√2 ≈ 7.07 cm

Bok tego kwadratu ma około 7.07 cm długości.

Praktyczne Zastosowania Wzoru na Przekątną Kwadratu

Wzór na przekątną kwadratu znajduje szerokie zastosowanie w różnych dziedzinach życia. Oto kilka przykładów:

Wyobraź sobie, że projektujesz ogród i chcesz zbudować kwadratową rabatę kwiatową. Znając długość boku rabaty, możesz szybko obliczyć długość przekątnej, aby wyznaczyć punkty, w których należy umieścić podpory. Albo jesteś stolarzem i potrzebujesz wykonać kwadratową ramę do obrazu. Wzór na przekątną kwadratu pomoże Ci dokładnie obliczyć wymiary ramy.

Dodatkowe Wskazówki i Triki

*Pamiętaj o jednostkach: Upewnij się, że wszystkie wymiary są podane w tej samej jednostce (np. centymetry, metry, cale) przed rozpoczęciem obliczeń. Inaczej wynik będzie błędny.

*Używaj kalkulatora: Jeśli potrzebujesz bardzo dokładnych obliczeń, użyj kalkulatora, który ma funkcję pierwiastka kwadratowego.

*Zapamiętaj przybliżoną wartość √2: Przybliżona wartość pierwiastka kwadratowego z 2 to 1.414. Pamiętanie tej wartości może być przydatne do szybkiego szacowania długości przekątnej w sytuacjach, gdy nie masz dostępu do kalkulatora.

*Przekształcaj wzór: W zależności od tego, co jest dane (długość boku lub długość przekątnej), możesz przekształcić wzór, aby obliczyć szukaną wartość.

Podsumowanie

Wzór na przekątną kwadratu (d = a√2) to potężne narzędzie, które pozwala szybko i łatwo obliczyć długość przekątnej, znając długość boku kwadratu. Jego wyprowadzenie opiera się na Twierdzeniu Pitagorasa, co pokazuje, jak powiązane są różne koncepcje matematyczne. Zastosowania tego wzoru są szerokie i obejmują wiele dziedzin życia, od budownictwa i architektury, po stolarstwo i informatykę.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć wzór na przekątną kwadratu i jego praktyczne zastosowania. Pamiętaj, że ćwiczenie czyni mistrza! Spróbuj rozwiązać kilka zadań i zobaczysz, jak szybko opanujesz tę wiedzę. Nie bój się geometrii – to fascynująca dziedzina, która może być bardzo przydatna w życiu!