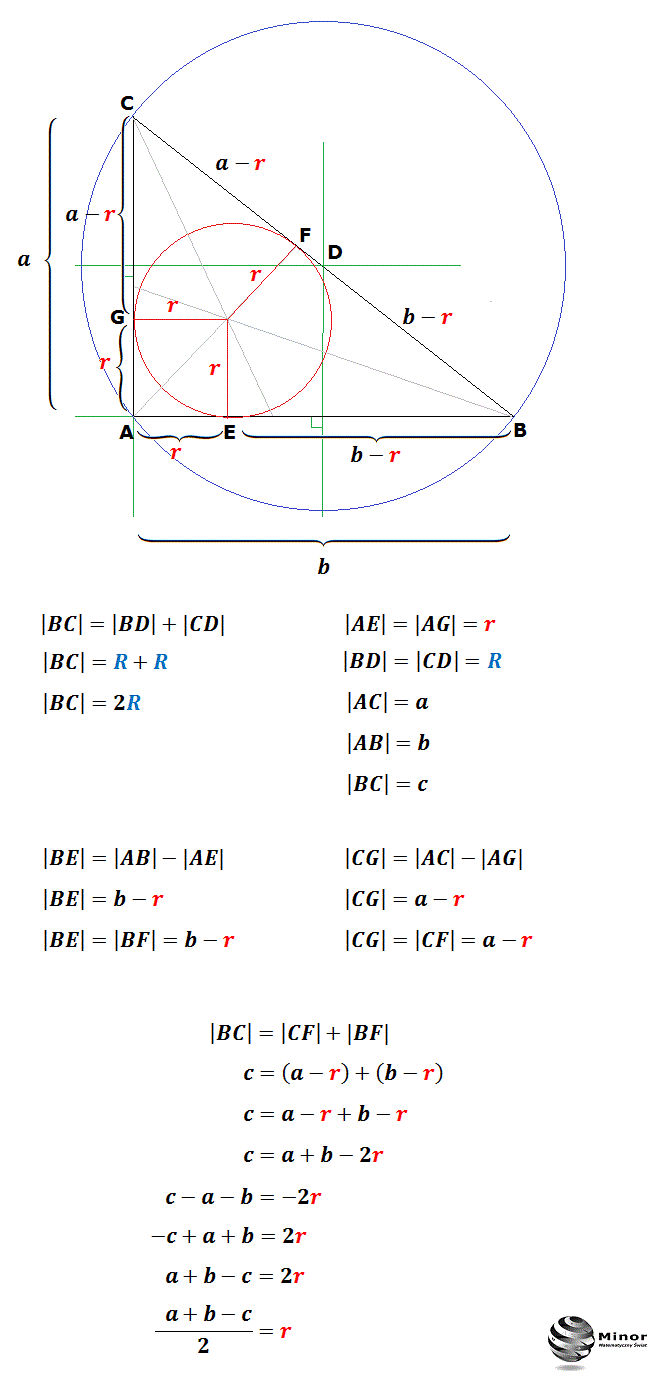
Wzór Na Promień Okręgu Wpisanego W Trójkącie Równoramiennym

Dzień dobry! Dzisiaj zajmiemy się obliczaniem promienia okręgu wpisanego w trójkąt równoramienny. Brzmi trochę skomplikowanie? Spokojnie, zaraz zobaczycie, że to wcale nie jest takie trudne.

Zacznijmy od podstaw. Trójkąt równoramienny, jak sama nazwa wskazuje, ma dwa boki równej długości, nazywane ramionami. Trzeci bok to podstawa. Okrąg wpisany w trójkąt to okrąg, który jest styczny do każdego z boków tego trójkąta. Promień takiego okręgu to odległość od środka okręgu do punktu styczności z dowolnym bokiem trójkąta.

Jak więc znaleźć ten promień? Istnieją różne sposoby, a wybór najlepszego zależy od tego, jakie dane o trójkącie znamy. Omówimy kilka popularnych metod.

Wzór z Polem i Połową Obwodu

Najbardziej uniwersalny wzór na promień okręgu wpisanego (oznaczmy go jako r) wykorzystuje pole trójkąta (oznaczmy je jako P) i połowę jego obwodu (oznaczmy ją jako p). Wzór wygląda następująco:

r = P / p

Żeby go użyć, musimy najpierw obliczyć pole trójkąta i połowę jego obwodu.

Obliczanie połowy obwodu (p):

Obwód trójkąta to suma długości wszystkich jego boków. W trójkącie równoramiennym mamy dwa ramiona (oznaczmy długość każdego z nich jako a) i podstawę (oznaczmy ją jako b). Zatem obwód trójkąta to a + a + b = 2a + b.

Połowa obwodu, p, to po prostu obwód podzielony przez 2:

p = (2a + b) / 2

Obliczanie pola trójkąta (P):

Obliczenie pola trójkąta może być nieco bardziej skomplikowane, ale i na to są sposoby.

Jeśli znamy wysokość (h) opuszczoną na podstawę: Wtedy pole trójkąta obliczamy ze wzoru:

P = (1/2) * b * h

Gdzie b to długość podstawy, a h to wysokość.
Jeśli znamy długości boków (a i b) i nie znamy wysokości: Możemy skorzystać ze wzoru Herona. W tym przypadku potrzebujemy już obliczonej wcześniej połowy obwodu (p). Wzór Herona wygląda tak:

P = √(p * (p - a) * (p - a) * (p - b))

Czyli pierwiastek kwadratowy z iloczynu połowy obwodu i różnic między połową obwodu a długościami każdego z boków.

Przykład:

Załóżmy, że mamy trójkąt równoramienny o ramionach długości a = 5 cm i podstawie długości b = 6 cm. Chcemy obliczyć promień okręgu wpisanego.

Obliczamy połowę obwodu (p):

p = (2 * 5 + 6) / 2 = (10 + 6) / 2 = 16 / 2 = 8 cm
Obliczamy pole trójkąta (P) za pomocą wzoru Herona:

P = √(8 * (8 - 5) * (8 - 5) * (8 - 6)) = √(8 * 3 * 3 * 2) = √(144) = 12 cm²
Obliczamy promień okręgu wpisanego (r):

r = P / p = 12 / 8 = 1.5 cm

Zatem promień okręgu wpisanego w ten trójkąt wynosi 1.5 cm.

Wykorzystanie funkcji trygonometrycznych

Jeśli znamy kąty trójkąta równoramiennego, możemy wykorzystać funkcje trygonometryczne do znalezienia wysokości, a następnie pola trójkąta. W trójkącie równoramiennym kąty przy podstawie są równe. Oznaczmy te kąty jako α. Kąt między ramionami oznaczmy jako β. Wiemy, że suma kątów w trójkącie wynosi 180 stopni, więc:

2α + β = 180°

Jeśli znamy jeden z kątów (α lub β), możemy obliczyć drugi.

Obliczanie wysokości (h):

Wysokość opuszczona na podstawę dzieli trójkąt równoramienny na dwa identyczne trójkąty prostokątne. Możemy użyć funkcji trygonometrycznej tangens (tan) do obliczenia połowy długości podstawy (b/2) w odniesieniu do wysokości (h) i kąta α:

tan(α) = h / (b/2)

Stąd:

h = (b/2) * tan(α)

Znając wysokość i długość podstawy, możemy obliczyć pole trójkąta jak poprzednio:

P = (1/2) * b * h

A następnie obliczyć promień okręgu wpisanego, korzystając ze wzoru r = P / p.

Przykład:

Załóżmy, że mamy trójkąt równoramienny o podstawie b = 10 cm i kącie przy podstawie α = 45°.

Obliczamy wysokość (h):

h = (10/2) * tan(45°) = 5 * 1 = 5 cm
Obliczamy długość ramienia (a) korzystając z twierdzenia Pitagorasa lub funkcji trygonometrycznych:

a = √(h² + (b/2)²) = √(5² + 5²) = √(50) = 5√2 cm
Obliczamy połowę obwodu (p):

p = (2 * 5√2 + 10) / 2 = 5√2 + 5 cm
Obliczamy pole trójkąta (P):

P = (1/2) * 10 * 5 = 25 cm²
Obliczamy promień okręgu wpisanego (r):

r = 25 / (5√2 + 5) = 5 / (√2 + 1)

Możemy usunąć niewymierność z mianownika, mnożąc licznik i mianownik przez (√2 - 1):

r = (5 * (√2 - 1)) / ((√2 + 1) * (√2 - 1)) = (5 * (√2 - 1)) / (2 - 1) = 5√2 - 5 cm

Zatem promień okręgu wpisanego w ten trójkąt wynosi 5√2 - 5 cm, co w przybliżeniu daje 2.07 cm.

Podsumowanie

Jak widzicie, istnieje kilka sposobów na obliczenie promienia okręgu wpisanego w trójkąt równoramienny. Wybór konkretnej metody zależy od dostępnych danych. Najważniejsze to zrozumieć zależności między bokami, kątami, wysokością i polem trójkąta. Pamiętajcie o dokładnym analizowaniu zadania i wyborze najprostszego i najbardziej efektywnego sposobu rozwiązania. Powodzenia!