Wzór Na Promień Okręgu Wpisanego W Trójkącie Prostokątnym

W artykule tym zgłębimy temat związany z geometrią trójkąta prostokątnego, skupiając się na obliczaniu promienia okręgu wpisanego w ten trójkąt. Jest to zagadnienie, które pojawia się zarówno w zadaniach szkolnych, jak i w bardziej zaawansowanych problemach matematycznych.

Promień okręgu wpisanego w trójkąt prostokątny, często oznaczany literą 'r', jest ściśle związany z długościami boków tego trójkąta. Znajomość wzoru na obliczenie tego promienia pozwala na szybkie i efektywne rozwiązywanie zadań geometrycznych.

Aby móc efektywnie operować wzorami i zrozumieć zależności, przyjmijmy oznaczenia: a i b oznaczają długości przyprostokątnych trójkąta prostokątnego, natomiast c oznacza długość przeciwprostokątnej. Promień okręgu wpisanego oznaczamy literą 'r'.

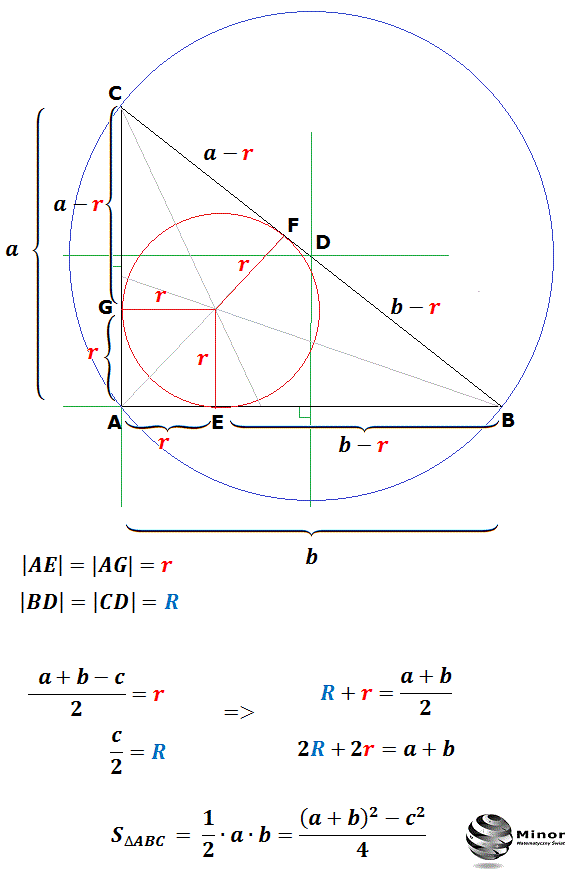
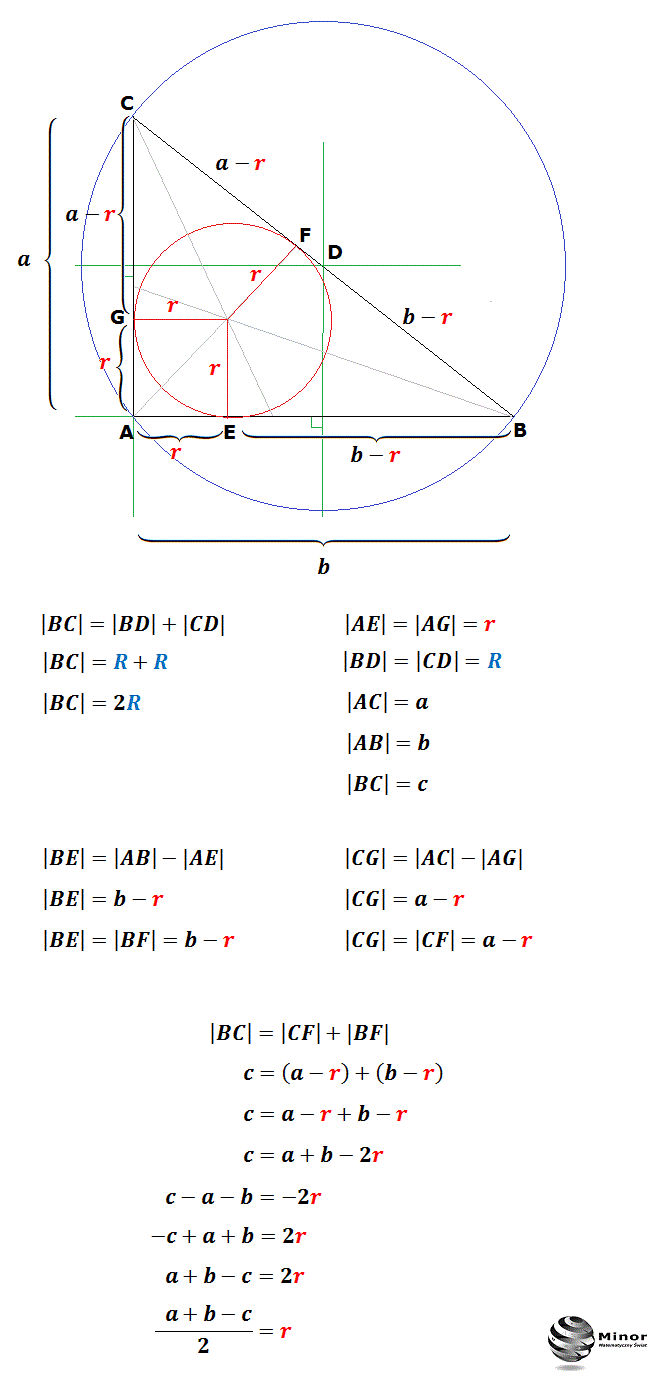
Podstawowy wzór, który pozwala na obliczenie promienia okręgu wpisanego w trójkąt prostokątny, wyraża się następująco:

r = (a + b - c) / 2

Wykorzystując ten wzór, możemy obliczyć promień okręgu wpisanego, mając dane długości boków trójkąta prostokątnego. Wzór ten wynika z relacji pomiędzy polem trójkąta, jego obwodem i promieniem okręgu wpisanego.

Zastanówmy się teraz nad kilkoma przykładami, aby lepiej zrozumieć zastosowanie tego wzoru.

Przykład 1: Rozważmy trójkąt prostokątny o przyprostokątnych długości a = 3 cm i b = 4 cm. Z twierdzenia Pitagorasa wiemy, że c = √(a² + b²) = √(3² + 4²) = √(9 + 16) = √25 = 5 cm. Zatem, promień okręgu wpisanego wynosi r = (3 + 4 - 5) / 2 = (7 - 5) / 2 = 2 / 2 = 1 cm.

Przykład 2: Weźmy trójkąt prostokątny o przyprostokątnych a = 5 cm i b = 12 cm. Wówczas, c = √(5² + 12²) = √(25 + 144) = √169 = 13 cm. Promień okręgu wpisanego wynosi r = (5 + 12 - 13) / 2 = (17 - 13) / 2 = 4 / 2 = 2 cm.

Przykład 3: Rozważmy trójkąt prostokątny o przyprostokątnych a = 8 cm i b = 15 cm. Wtedy c = √(8² + 15²) = √(64 + 225) = √289 = 17 cm. Promień okręgu wpisanego wynosi r = (8 + 15 - 17) / 2 = (23 - 17) / 2 = 6 / 2 = 3 cm.

Widzimy, że wzór jest prosty w użyciu i pozwala na szybkie wyznaczenie promienia okręgu wpisanego, pod warunkiem, że znamy długości wszystkich boków trójkąta prostokątnego.

Związek z polem trójkąta

Pole trójkąta prostokątnego, oznaczane zwykle jako P, możemy obliczyć na kilka sposobów. Jednym z nich jest skorzystanie z długości przyprostokątnych: P = (a * b) / 2. Innym sposobem, który wykorzystuje promień okręgu wpisanego, jest wzór P = r * p, gdzie p to połowa obwodu trójkąta (tzw. "półobwód"). W przypadku trójkąta prostokątnego, p = (a + b + c) / 2. Zatem, możemy zapisać równanie: (a * b) / 2 = r * (a + b + c) / 2. Mnożąc obie strony przez 2, otrzymujemy a * b = r * (a + b + c).

Przekształcając wzór r = (a + b - c) / 2, otrzymujemy 2r = a + b - c, a stąd c = a + b - 2r. Podstawiając to do wzoru na pole trójkąta wyrażonego za pomocą promienia okręgu wpisanego i półobwodu, otrzymujemy:

a * b = r * (a + b + a + b - 2r) a * b = r * (2a + 2b - 2r) a * b = 2r * (a + b - r)

Ten wzór pokazuje związek pomiędzy długościami przyprostokątnych, promieniem okręgu wpisanego i polem trójkąta. Możemy go użyć do wyprowadzenia innych zależności lub do weryfikacji poprawności obliczeń.

Inne metody wyznaczania promienia

W niektórych przypadkach, gdy nie znamy bezpośrednio długości wszystkich boków trójkąta, a jedynie inne jego parametry (np. kąty ostre i długość jednego boku), możemy wykorzystać funkcje trygonometryczne (sinus, cosinus, tangens) do wyznaczenia długości pozostałych boków, a następnie zastosować podstawowy wzór na promień okręgu wpisanego.

Przykładowo, jeśli znamy kąt ostry α i długość przyprostokątnej a, możemy obliczyć długość drugiej przyprostokątnej b korzystając z tangensa: tan(α) = a / b, a stąd b = a / tan(α). Długość przeciwprostokątnej c możemy obliczyć korzystając z cosinusa: cos(α) = b / c, a stąd c = b / cos(α). Po wyznaczeniu długości wszystkich boków, możemy zastosować wzór r = (a + b - c) / 2.

Warto pamiętać, że znajomość zależności trygonometrycznych jest niezbędna do rozwiązywania tego typu problemów.

Ponadto, w zadaniach, gdzie podane jest pole trójkąta i długość jednego z boków, możemy wykorzystać wzór na pole trójkąta P = (a * b) / 2 do wyznaczenia długości drugiej przyprostokątnej. Następnie, korzystając z twierdzenia Pitagorasa, obliczamy długość przeciwprostokątnej i stosujemy wzór na promień okręgu wpisanego.

Znajomość różnych metod i wzorów pozwala na elastyczne podejście do rozwiązywania problemów związanych z trójkątem prostokątnym i okręgiem wpisanym. Kluczem do sukcesu jest zrozumienie zależności pomiędzy poszczególnymi elementami trójkąta i umiejętne wykorzystywanie odpowiednich wzorów.